Théorèmes de l'alternative - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Les théorèmes de l'alternative, dont le plus fameux est le lemme de Farkas, concernent tous un système d'inéquations linéaires dans un espace vectoriel réel de dimension finie. Il s'agit de donner un critère permettant de trancher si le système est ou non consistant, c'est-à-dire s'il admet ou non une solution (ou, pour ceux dont 0 est une solution évidente, une solution non nulle).
Le principe en est à chaque fois le suivant : face à un système d'inéquations, on peut opérer des combinaisons linéaires de ces inéquations à coefficients positifs ou nuls, qui sont alors toutes des conséquences du système (l'usage judicieux de coefficients strictement positifs permettant au cas par cas de produire des conséquences qui soient des inégalités strictes). Il est bien évident que si l'une de ces conséquences est une absurdité – typiquement 0 < 0 – le système initial ne peut avoir de solution. Or, il se trouve que cette condition suffisante pour que le système soit inconsistant est à chaque fois nécessaire : chacun des théorèmes ci-dessous en exprime une variante.
Le nom de « théorèmes de l'alternative » vient du fait que la condition nécessaire et suffisante a, elle aussi, la forme d'un problème de recherche de solutions pour un système mêlant équations et inéquations. On se retrouve donc en parallèle avec deux systèmes, dont un et un seul a des solutions. Traduites en termes de matrices, les deux branches de l'alternative ont des formulations du même esprit, voire étonnamment semblables dans le cas du théorème de Ville.
Systèmes d'inéquations strictes et systèmes d'inéquations larges : les théorèmes de Gordon et de Stiemke
Le théorème de Gordan
Il couvre le cas d'un système d'inéquations toutes strictes, de la forme :
où les fj sont des formes linéaires sur un espace vectoriel réel E de dimension finie.
Il y a une obstruction évidente à l'existence de solutions pour un tel système : si on fait une combinaison linéaire à coefficients positifs non tous nuls de cette famille d'inéquations, on obtient une nouvelle inéquation stricte vérifiée par toutes les solutions. Si on peut ajuster les coefficients de cette combinaison linéaire de façon à obtenir l'inéquation absurde 0 > 0, c'est que le système était inconsistant.
Le théorème de Gordan assure que, à partir de tout système inconsistant, on peut ainsi produire l'inéquation 0 > 0 :
Théorème de Gordan (1873) — Soit 
des formes linéaires sur un espace vectoriel réel de dimension finie E. Alors :
si et seulement si
- il existe une écriture
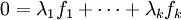à coefficients tous positifs ou nuls dont l'un au moins n'est pas nul.
Le théorème de Stiemke
Il concerne les systèmes d'inéquations linéaires au sens large :
.
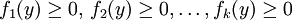Son énoncé est précisément le suivant :
Théorème de Stiemke (1913) — Soit 
des formes linéaires sur un espace vectoriel de dimension finie E. Alors :
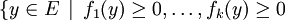, l'une au moins de ces inégalités étant stricte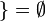
si et seulement si
- il existe une écriture
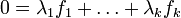à coefficients tous strictement positifs.
Cet énoncé est rendu un peu plus difficile à lire que les autres théorèmes de la série à cause de la technicité « l'une au moins de ces inégalités étant stricte » ; la raison d'être de celle-ci est que les systèmes d'inéquations larges ne peuvent être complètement inconsistants : ils comptent au moins 0 parmi leurs solutions, et au-delà tous les points qui vérifient le système d'équations linéaires correspondant. D'où la nécessité de compliquer un peu la forme du système en ne considérant pas comme des solutions significatives celles qui sont dans l'intersection des noyaux de toutes les formes fj.
Preuve du théorème de Gordan
Parmi tous les théorèmes considérés dans cette page, le théorème de Gordan est celui où la preuve contient le moins de technicités supplémentaires. On peut la fonder sur un théorème de séparation des convexes (celui parfois appelé « deuxième forme géométrique du théorème de Hahn-Banach ») ou par le théorème de projection sur un convexe fermé. C'est ce dernier choix qui est fait ici.
Comme il est souvent pratique pour faire des manipulations dans un dual, munissons E d'une structure euclidienne ; pour chaque indice j, il existe dès lors un vecteur sj unique de E qui permette d'écrire pour tout y : fj(y) = < sj | y > .
Considérons le convexe compact K enveloppe convexe des k points sj et notons y0 = πK(0) la projection orthogonale de 0 sur ce fermé de E. On sait que pour tout s de K (et en particulier pour les sj) on dispose de l'inégalité :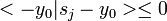 
qu'on regroupe en 
.
Entrons dans le vif de la preuve de Gordan. Comme pour tous les théorèmes de l'article, l'implication montante est évidente. Montrons donc l'implication descendante, en supposant le système d'inégalités strictes inconsistant. En particulier y0 n'en est alors pas solution, donc il existe un j pour lequel 
. D'où 
, puis y0 = 0, ce qui prouve bien que 0 appartient à K, et est donc combinaison linéaire à coefficients positifs des sj.
Le théorème de Gordan entraîne le théorème de Stiemke
On peut donner une démonstration directe du théorème de Stiemke en appelant de nouveau la théorie de la séparation des convexes. Il est toutefois instructif de s'apercevoir que c'est un théorème « dual » du théorème de Gordan, et qu'on peut l'en déduire par des manipulations algébriques simples à défaut d'être naturelles.
On reverra ces mêmes manipulations présentées sous forme matricielle plus loin, en énonçant le théorème de Villé. Elles reposent sur une idée importante qu'on retrouve notamment à la base de la théorie du problème dual en programmation linéaire : la deuxième branche de l'équivalence dans le théorème de Stiemke, qui est en première lecture un mélange d'inéquations strictes (les conditions 0 < λj) et d'une équation vectorielle (la condition 
) peut, avec un peu de doigté, être transformée en une simple collection d'inéquations strictes, à laquelle on peut appliquer le théorème de Gordan. Stiemke apparaît finalement comme une réécriture de Gordan où les emplacements des deux énoncés équivalents se retrouvent intervertis.
On commence par extraire de 
une famille libre maximale ; quitte à renuméroter, on suppose que c'est 
. On la complète arbitrairement en une base 
de E * et enfin on note 
la base de E dont est la base duale. On a donc, pour tout i entre 1 et n et tout j entre 1 et p la relation fj(ei) = δij (symbole de Kronecker) ; comme les fj pour j entre p + 1 et k sont des combinaisons linéaires des premiers fj, toutes les formes fj s'annulent sur tous les ei d'indices 
.
Une fois ces notations posées, lançons nous dans la preuve de Stiemke. Comme dans chaque énoncé, l'implication montante est évidente. Prouvons l'autre par contraposition, en supposant donc que 0 ne peut pas être écrit sous la forme avec des λj tous strictement positifs, dans le but de construire un y solution du système d'inéquations.
Une relation entre applications linéaires est vraie, si et seulement si, elle est vraie en tout vecteur d'une base donnée ; on peut donc remarquer que :
Le système 
n'a pas de solutions.
Insérons dans ce système les informations sur les fj(ei), on sait ainsi que :
Le système 
n'a pas de solutions.
Point crucial de la preuve, l'inconsistance du système mixte d'inéquations et équations qui précède peut se réexprimer comme inconsistance d'un système plus simple ne comprenant plus que des inéquations :
Le système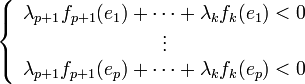 
n'a pas de solutions.
La forme de ce système rentre dans le cadre du théorème de Gordan. Il existe donc des réels positifs ou nuls 
, dont au moins un n'est pas nul, avec lesquels on peut construire une combinaison linéaire nulle des formes apparaissant dans le système qui précède. En annulant successivement le coefficient de chaque λj, on constate que :
- pour tout indice i entre p + 1 et k,
.
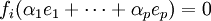Il découle par ailleurs des relations fj(ei) = δij que
- pour les indices i entre 1 et p,
.
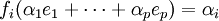Posons alors 
. On s'aperçoit alors qu'on vient de construire avec ce vecteur une solution non triviale du système d'inéquations objet de l'énoncé du théorème de Stiemke.