Théorème spectral - Définition

Introduction

Un ellipsoïde en trois possède autant d'axes de symétrie que l'espace de dimensions. Ils sont notés ici x, y et z.

En mathématiques, une quadrique désigne une surface d’un espace euclidien. Elle est définie par un polynôme du second degré dont les variables correspondent aux coordonnées d’un vecteur dans une base orthonormale. L’ellipsoïde ou l’hyperboloïde à une ou deux nappes en sont des exemples. Cette définition s’étend à toutes les dimensions finies et se généralise aux nombres complexes. Une symétrie axiale est une transformation de l’espace. À chaque point est associé le point en vis-à-vis par rapport à un axe dit de symétrie. Le point de départ et d'arrivée définissent une droite perpendiculaire, sécante à cet axe et l’intersection correspond au milieu des points de départ et d'arrivée.

Les quadriques possèdent une propriété remarquable, il existe au moins autant d’axes de symétries que l’espace contient de dimensions. De plus, ces axes peuvent être choisis perpendiculaires entre eux. Il existe des cas pathologiques invalidant ce résultat, comme le paraboloïde elliptique. Ces quadriques, qualifiées de dégénérées par les mathématiciens, possèdent moins d’axes de symétries.

Ce même résultat s’exprime fort différemment selon le contexte utilisé. Il possède un équivalent en terme algébrique, linéaire ou bilinéaire et encore matriciel. Son champ d’application dépasse celui de l’algèbre et la géométrie. En mathématiques pures, il est utilisé pour résoudre des équations différentielles ou classifier les forme quadratiques, il est aussi appliqué au calcul numérique et aux statistiques. La physique en fait grand usage pour des questions de mécanique générale du solide ou du point.

Cette propriété apporte une réponse restée conjecturale plus d’un siècle, avant d’être démontrée par Karl Weierstrass en 1858. Elle était nécessaire pour répondre à une question d’astronomie : la stabilité du système solaire. Si elle s’est avérée insuffisante pour une réponse complète, ce résultat eut néanmoins un brillant avenir. La généralisation à la dimension infinie ouvre une vaste théorie, dite spectrale. Elle est indispensable à la physique du XX^e siècle, par exemple pour la mécanique quantique. Pour cette raison, ce résultat porte parfois le nom de théorème spectral.

Dimension algébrique de la propriété

La sphère rouge représente la sphère unité pour la première forme, la figure bleue représente la sphère unité pour la deuxième forme dans la mesure ou celle-ci est définie positive. La figure bleue est un ellipsoïde dont les axes sont orthogonaux pour la première forme.

Une quadrique est un objet structurant, un cas particulier essentiel est celui de la sphère, définir un tel objet dans un espace vectoriel revient à le munir d'une distance spécifique, dite euclidienne. Une méthode couramment utilisée consiste à utiliser une forme quadratique, c'est-à-dire une application de l'espace dans l'ensemble des réels positifs. La distance est définie comme la racine carrée de la forme quadratique du vecteur reliant les deux points. Utiliser la forme quadratique à la place de la distance est commode. Les racines carrées disparaissent, permettant une expression plus simple des formules. Ainsi, le théorème de Pythagore dans le plan s'écrit, si Φ est la forme quadratique associée à la distance et si θ₁ et θ₂ correspondent aux carrés des coordonnées dans une base orthonormale, par Φ = θ₁ + θ₂. Dans le cas d'une dimension finie quelconque : Φ = θ₁ + θ₂ + … + θ_n.

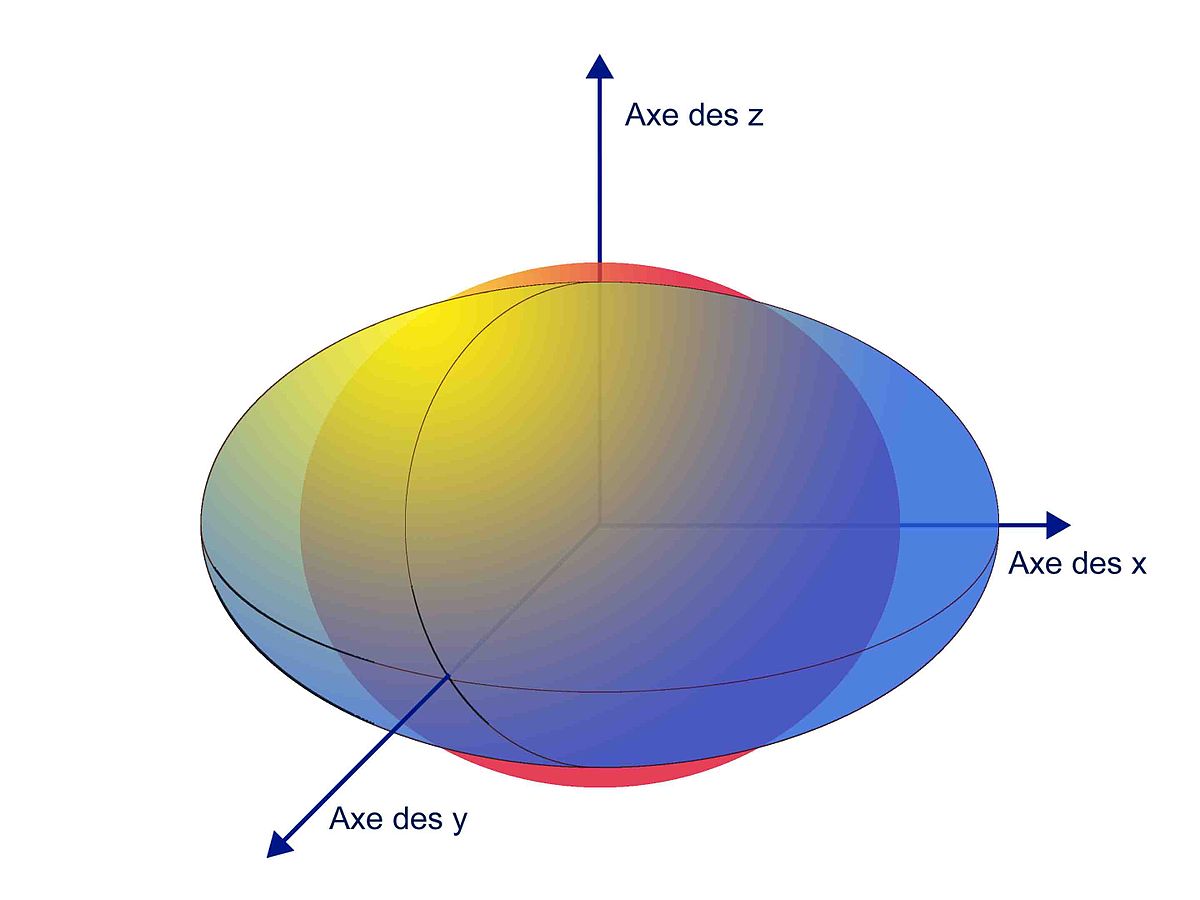
Une telle forme correspond à un cas particulier de quadrique. Elle est aussi définie par un polynôme de degré deux. Il est néanmoins homogène, c'est-à-dire qu'il ne contient que des termes de degré deux. Une quadrique homogène définit une deuxième forme quadratique Ψ et en conséquence une autre distance. Graphiquement, le contexte de la propriété de l'article est illustré par la figure de gauche. La distance d'origine est définie par la sphère rouge et celle de la quadrique associée à Ψ, par l'ellipsoïde bleu. Il existe alors une base qui respecte l'orthogonalité des deux formes quadratiques. Si l'orthogonalité est respectée, il n'en est pas de même pour les longueurs. Ainsi, le vecteur unitaire de l'axe des x pour la distance originale (en rouge) est de longueur plus petite pour la nouvelle distance (en bleu), d'où la nécessité d'un coefficient s₁ pour passer d'une distance à l'autre.

Seules les ellipsoïdes définissent une distance euclidienne. Un hyperboloïde définit une distance de nature différente, utilisée par exemple pour la relativité restreinte.

C'est en ces termes que Weierstrass exprime son théorème. Le vocabulaire évolue un peu avec le temps, le terme maintenant utilisé est celui de forme quadratique quand il parle de fonction homogène du second degré :

« Soit deux fonctions homogènes du second degré Φ, Ψ de n variables x₁, x₂, …. , alors il est en général possible, de les représenter de cette même forme

Φ = θ₁ + θ₂ + … + θ_n

Ψ = s₁θ₁ + s₂θ₂+…+s_nθ_n,

θ₁, θ₂, …,θ_n étant des expressions quadratiques homogènes des x₁,…x_n et s₁,… , s_n des constantes. »

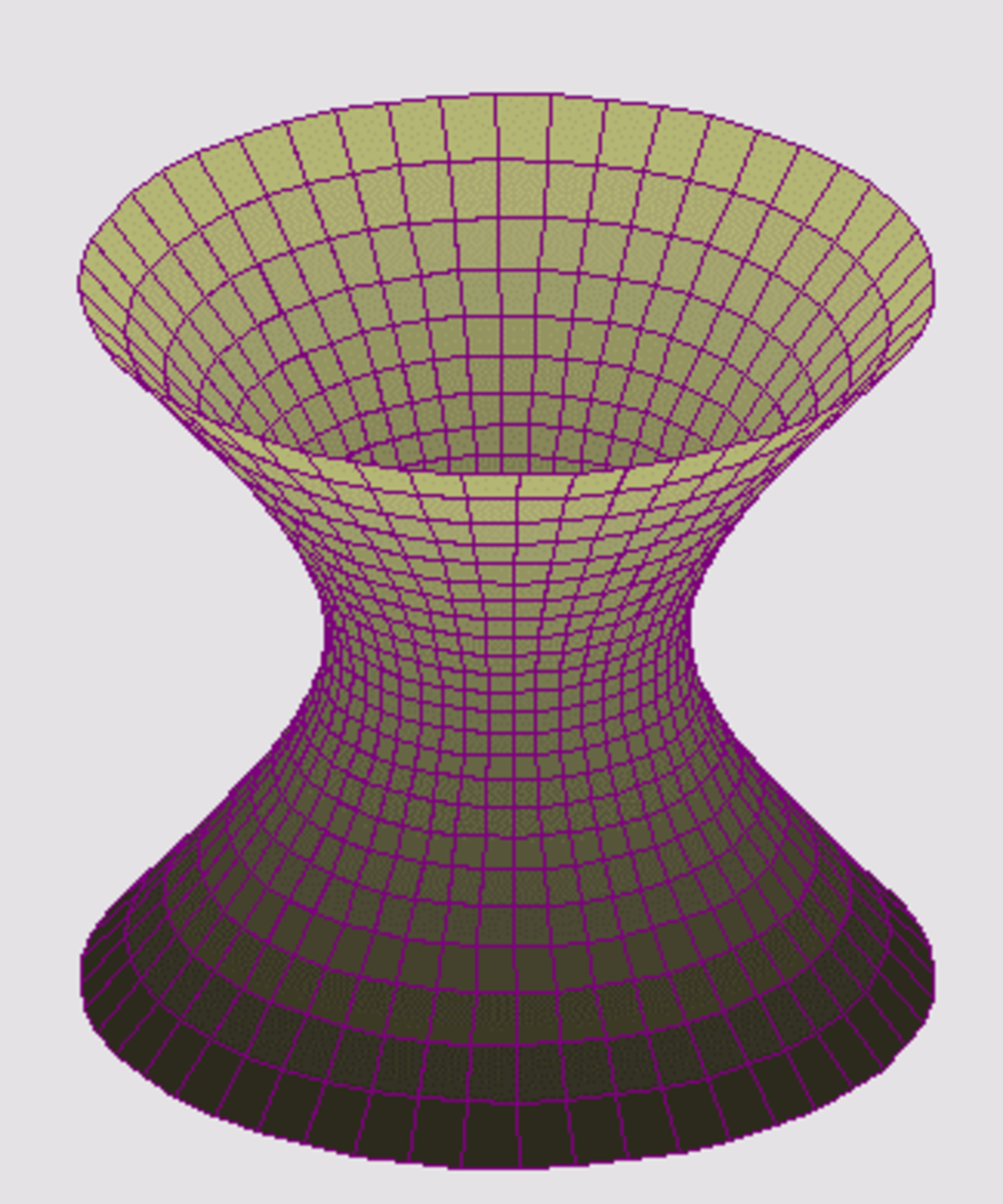
Un tel formalisme généralise la notion de distance. Les valeurs de s_i n'ont aucune raison d'être toutes positives. Si tel n'est pas le cas, la sphère unité prend une apparence différente, analogue à un hyperboloïde. Une telle géométrie est utilisée en physique, dans le cadre de la relativité restreinte.

Enfin, il existe un pont entre les formes quadratiques et les applications linéaires, construit à l'aide du produit scalaire. Il est ici noté < . , . >, c'est-à-dire que le produit scalaire de deux vecteurs u et v est noté < u , v >. A une application linéaire a de l'espace dans lui-même (appelé endomorphisme), est associé la forme quadratique Φ_a définie par Φ_a(u) = < a(u) , u >. Il existe de bons endomorphismes pour définir les formes quadratiques, ils sont nommés autoadjoints. Ils correspondent à ceux dont la matrice, dans une base orthonormée est symétrique, c'est-à-dire que les coefficients sont en miroir par rapport à la première diagonale. L'étude des endomorphismes autoadjoints est l'origine de la question traitée dans cet l'article.