Théorème spectral - Définition
La liste des auteurs de cet article est disponible ici.
Applications
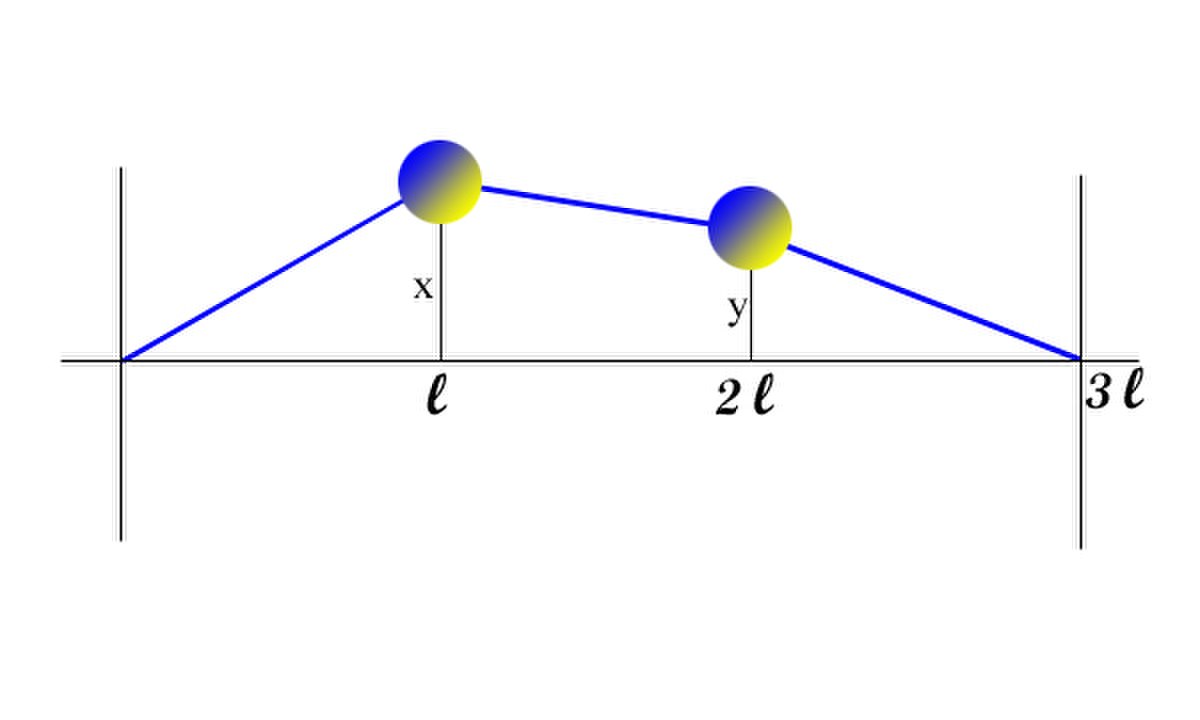
Pendule de D'Alembert à deux boules
![](https://static.techno-science.net/illustration/Definitions/1200px/p/pendule-de-d-alembert-deux-boules_cb036ebb5d5a0657691d6395b55ae66f.jpg")
D'Alembert, dans la deuxième édition de son traité de dynamique, propose de résoudre l'équation du pendule illustré sur la figure de droite. La corde est élastique et de masse nulle, les deux parois sur lesquelles elle est maintenue est fixe. Enfin, les oscillations des deux masses, dont les coordonnées verticales sont notées x et y, sont petites devant l. Les deux boules sont régulièrement espacées et de même masse. Dans ce contexte la première masse reçoit une force verticale, proportionnelle à -2x + y et la deuxième à -2y + x.
Si E est l'espace vectoriel des couples (x, y), f la fonction du temps à valeur dans E décrivant la trajectoire du pendule, a l'endomorphisme défini par la matrice suivante, il existe une constante k tel que :
L'endomorphisme a dispose d'une matrice réelle symétrique, il est donc autoadjoint. L'existence d'une base orthonormée diagonalisant a permet de séparer les variables et donc de résoudre l'équation différentielle. D'Alembert, qui ne dispose pas de ce formalisme, utilise le théorème grâce à la méthode d'Euler dite des coefficients indéterminés. Elle se fonde sur l'utilisation du changement de variable suivant, si λ est un réel :
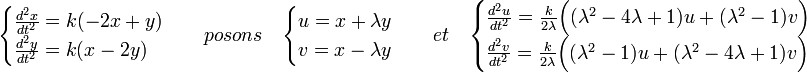
Choisir pour valeur de λ un permet de séparer les variables, le système devient :
En terme moderne, u et v correspondent à deux vecteurs propres de a formant une base orthonormale dont les coordonnées dans la base canonique est 2/√2 (1, 1) et 2/√2 (-1, 1).
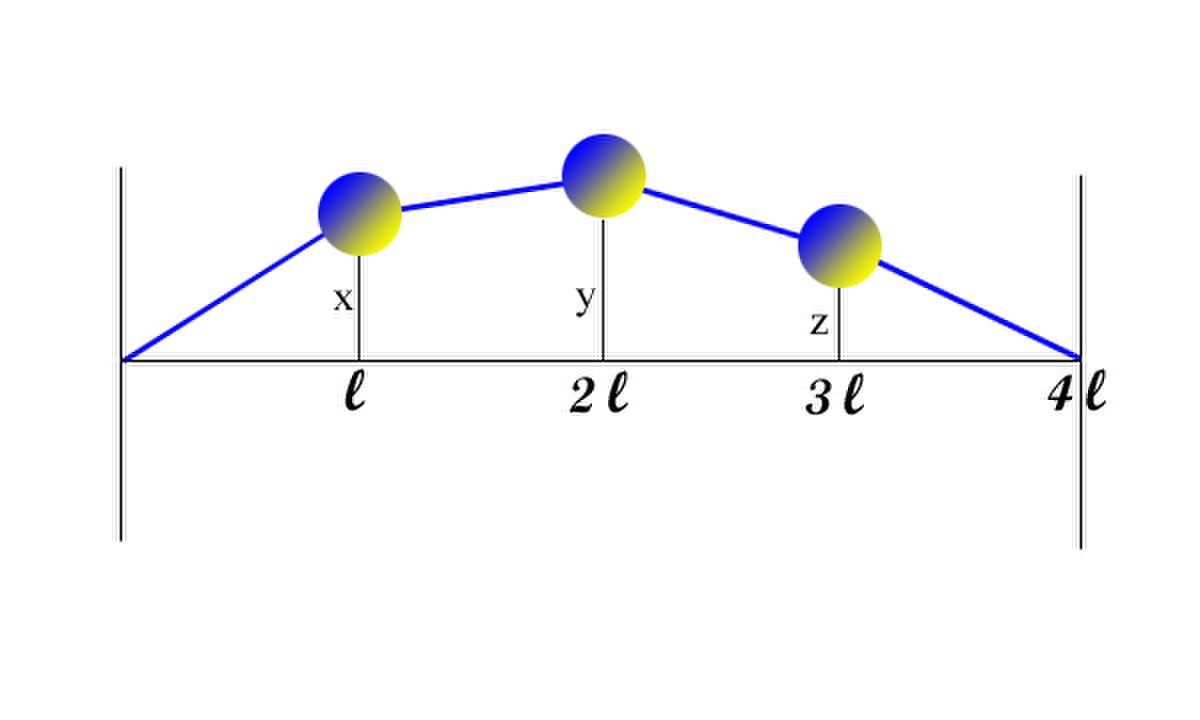
Pendule de D'Alembert à trois boules
![](https://static.techno-science.net/illustration/Definitions/1200px/p/pendule-de-d-alembert-trois-boules_71a689fa05ee6ee6214b0f7f5ddc187b.jpg")
Les hypothèses et notations sont équivalentes à celles du paragraphe précédent, l'espace vectoriel E est maintenant celui des triplets (x, y, z).
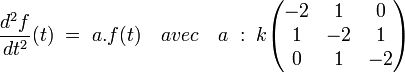
Il existe une base de vecteurs propres orthonormaux, d'après le théorème de l'article. Le calcul du polynôme caractéristique P[X] donne les valeurs propres λ1, λ2 et λ3 :
![P[X] = k^3(X+2)(X^2 + 4X +2) \quad donc \quad \lambda_1 = -2 \, , \, \lambda_2 = -2 + \sqrt 2 \; et \; \lambda_3 = -2 - \sqrt 2](https://static.techno-science.net/illustration/Definitions/autres/0/0ac181828bdcb682eba64e5b29851ce6_652d286fe4eee5fda74336ec577283fa.png){kind=small}
On en déduit les trois vecteurs propres associées v1, v2 et v3:
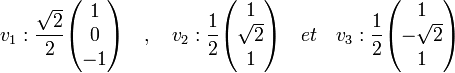
Classification des quadriques
Cas d'une quadrique homogène
![](https://static.techno-science.net/illustration/Definitions/1200px/h/hyperb2n_2686af3c1f9cb84cf42d236a9d95758d.png")
Si l'approche algébrique est la plus générale et la plus concise, la géométrie permet néanmoins d'établir certains résultats. Cette voie fût celle de Cauchy. L'article utilise la formalisation moderne issue de la géométrie différentielle, relativement différente de celle analytique du XIXe siècle.
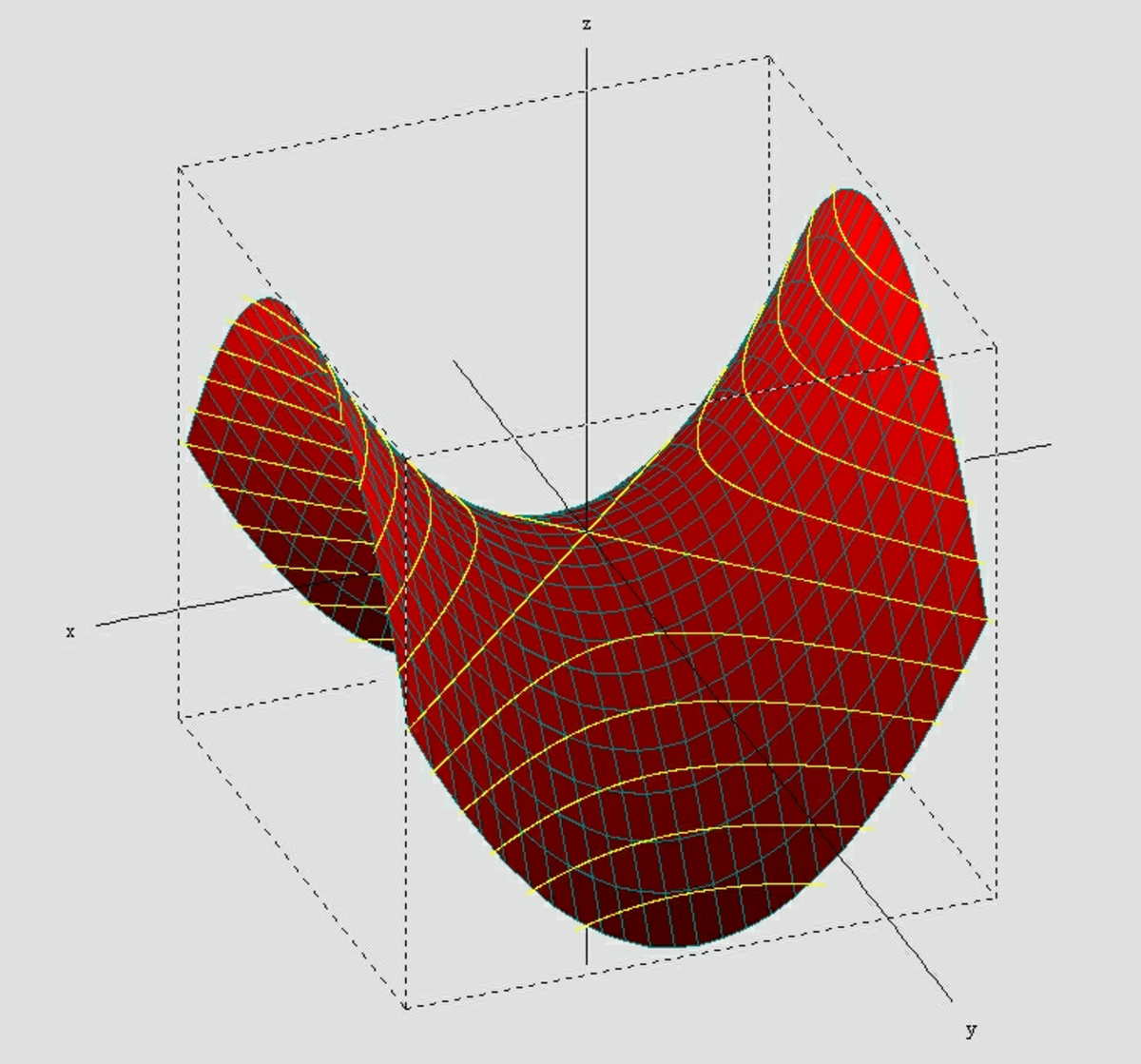
Soit E un espace vectoriel euclidien de dimension n (ei) une base orthonormale B de E et S une surface quadrique définie par une forme quadratique Ψ. L'objectif est d'étudier les extrema de Ψ sur la variété différentielle qu'est la sphère de rayon l'unité. Ici le terme d'extremum de la quadrique désigne un point de cette nature, elle permet de trouver des axes de symétries même si un tel axe ne croisent pas la surface, comme dans le cas de l'hyperboloïde à deux nappes.
Axe de symétrie et vecteur propre — Un vecteur u de la sphère unité correspond à un extremum local pour la forme Ψ si et seulement s'il est vecteur propre de l'endomorphisme autoadjoint a associé à la forme Ψ. Un tel vecteur est la direction d'un axe de symétrie de la quadrique.
En effet, la fonction Ψ ainsi que la sphère en tant que variété différentielle sont de classe C∞, les extrema se caractérisent donc par des annulations de différentielles. Plus précisément, u est un extremum local si et seulement si le noyau de Ψ est inclus dans l'espace tangent à la sphère au point u.
La sphère est l'image réciproque de {1} par l'application qui à un vecteur v associe < v , v >. La différentielle de cette application en v est la forme linéaire qui au vecteur h associe 2<v , h >. Son noyau est donc l'hyperplan orthogonal de v. Soit a l'endomorphisme autoadjoint associé à la quadrique, Ψ est alors l'application qui à un vecteur v associe < a(v) , v >. Sa différentielle en u est l'application qui, à un vecteur h, associe le scalaire DΨu(h) égal à 2< a(u) , h >.
Comme u est un vecteur extremum, DΨu est nul sur l'hyperplan orthogonal de u, le vecteur a(u) est donc orthogonal à l'orthogonal de u, ce qui signifie qu'il est colinéaire à u. C'est bien la définition d'un vecteur propre.
Réciproquement, si u est un vecteur propre, alors le théorème précédent sur les endomorphismes autoadjoints montre que l'orthogonal de u est stable par a et donc que le noyau de DΨu est bien l'orthogonal de u, ce qui montre que le vecteur est un extremum.
Montrons enfin que u définit un axe de symétrie de la quadrique. Soit v un vecteur quelconque de la quadrique. v est somme d'un vecteur colinéaire à u et d'un vecteur w orthogonal : v = α.u + h. Si λ est la valeur propre de u, alors l'image ω de w par la symétrie axiale de direction u est ω = α.u - h. Il suffit alors de montrer que Ψ(ω) est égal à Ψ(v). Cette propriété est une conséquence directe du fait que u est orthogonal à h :
Les résultats algébriques précédents permettent de conclure :
Existence de n axes de symétries — Toute quadrique homogène possèdent n axes de symétries orthogonaux deux à deux.
En effet, il existe une base orthogonale de vecteurs propres de a.
Cas d'une quadrique non dégénérée
Si le cas réellement intéressant est celui que la quadrique homogène, à cause de sa dimension algébrique. Il n'est pas inutile que classifier les quadriques. Dans le cas général, une quadrique comporte aussi des termes d'ordre un, le polynôme est alors la somme d'une forme quadratique, d'une forme linéaire et d'une constante. En utilisant les notations précédentes il existe alors un vecteur b tel que la quadrique possède pour image d'un vecteur v quelconque < a(v) , v > + < b , v > - c. Si l'application a est un automorphisme, c'est-à-dire s'il est bijectif, alors la forme quadratique associée ainsi que la quadrique sont qualifiées de non dégénérée. Un simple changement de l'origine permet de se ramener à la situation précédente.
Supposons a bijectif, alors 1/2.b admet un antécédent β par a. Le polynôme P prend la forme suivante :
![\forall v \in E \quad P[v] \, = \, <a(v) \, , \, v> \, + \, 2<a(\beta) \, , \, v> \, + \, <a(\beta) \, , \, a(\beta)> \, - \, <a(\beta) \, , \, a(\beta)> - c](https://upload.wikimedia.org/math/0/0/b/00b941f354310afc99cc998fc5c1da42.png)
On en déduit l'égalité :
![\forall v \in E \quad P[v] \, = \, <a(v + \beta) \, , \, v + \beta> - \; c_1 \quad avec \quad c_1 \,= \, c \ + \,, <a(\beta) \, , \, a(\beta)>](https://upload.wikimedia.org/math/4/4/5/4450eb03e6636938829354cc63b03fe7.png)
La situation est donc géométriquement analogue à la précédente.
Cas général
![](https://static.techno-science.net/illustration/Definitions/1200px/p/parabhyper_798fc48974df5e3665ab68236913d28e.png")
L'analyse précédente permet d'établir une rapide classification des quadriques. Le cas général est entièrement traité si le vecteur b est dans l'image de l'endomorphisme a. Il correspond à une équation de la forme :
ε désigne ici un entier égal à zéro ou à un. La base dans laquelle les coordonnées s'expriment est orthogonale mais n'est plus normée, la norme des vecteurs est choisie pour égaler à un ou son inverse les coefficients de la quadrique. La quadrique est non dégénérée si et seulement si j est égal à n.
Dans le cas ou la quadrique est dégénérée et ou b n'est pas dans le noyau de l'endomorphisme a. Il est alors possible de choisir comme dernier vecteur de la base un élément de la droite de direction b. Et, quitte à translater l'origine, il existe encore une base orthogonale tel que l'équation de la quadrique prenne la forme suivante :
Dans ce cas j est toujours strictement plus petit que n, les vecteurs propres de la forme quadratique ne sont plus toujours des axes de symétrie comme le montre le paraboloïde de l'introduction. Pour cette raison, et pour obtenir un vocabulaire parfaitement générique, on appelle axe principal toute droite passant par l'origine (une fois la translation réalisée) et de direction une droite de vecteurs propres.