Théorème isopérimétrique - Définition

Introduction

En géométrie, un théorème isopérimétrique traite d'une question concernant les compacts d'un espace métrique muni d'une mesure. Un exemple simple est donné par les compacts d'un plan euclidien. Les compacts concernés sont ceux de mesures finies ayant une frontière aussi de mesure finie. Dans l'exemple choisi, les compacts concernés sont ceux dont la frontière est une courbe rectifiable, c'est-à-dire essentiellement non fractale. Les mesures du compact et de sa frontière sont naturellement différentes, dans l'exemple choisi, la mesure du compact est celle d'une surface, celle de la frontière, une longueur.

Un théorème isopérimétrique caractérise les compacts ayant la mesure la plus grande possible pour une mesure de leur frontière fixée. Dans le plan euclidien en utilisant la mesure de Lebesgue, un théorème isopérimétrique indique qu'un tel compact est un disque. En dimension 3, toujours avec une géométrie euclidienne, une autre version du théorème indique que c'est une sphère. D'une manière plus générale, dans un espace euclidien de dimension n, muni de la mesure de Lebesgue, l'optimum est obtenu par une sphère, ce qui donne l'inégalité isopérimétrique suivante, si K est un compact et B la boule unité :

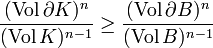
Un autre exemple de résultat est obtenu si le choix de la mesure est celui du nombre de points d'un réseau inclus dans le solide K, et si les compacts choisis sont des polytopes convexes à sommets entiers. En dimension 2 si le réseau est Z², on trouve le théorème de Pick, indiquant que la mesure du polytope P (c'est-à-dire le nombre de points de Z² qu'il contient) est égale à sa surface plus la moitié des points que contient sa surface plus un.

Un théorème isopérimétrique est souvent difficile à établir. Même un cas simple, comme celui du plan euclidien muni de la mesure de Lebesgue, est relativement technique à démontrer. Une des méthodes partielles de preuve, connue depuis la démonstration de Hurwitz en 1901 est d'utiliser un résultat d'analyse, issu de la théorie des séries de Fourier, connu sous le nom d'inégalité de Wirtinger. Le résultat reste partiel car il ne traite que des surfaces dont la frontière est une courbe de classe C¹.

Les théorèmes isopérimétriques sont actuellement l'objet d'une intense recherche en mathématiques, en particulier en analyse fonctionnelle et en théorie des probabilité, suite à leurs liens étroits avec les phénomènes de concentration de la mesure.

Une approche plus élémentaire est proposée dans l'article Isopérimétrie.

Fragments d'histoire

Prémisses

La connaissance de théorème isopérimétrique est ancienne, près de 3 000 ans. Le résultat essentiel de l'époque est l'œuvre de Zénodore qui démontre un résultat que l'on exprimerait maintenant de la manière suivante : S'il existe un polygone à n côtés de surface maximale à périmètre donné, alors il est régulier. Cette partie de l'histoire est traitée dans l'article Isopérimétrie. Les études des théorème isopérimétriques datant de l'antiquité se fonde exclusivement sur la géométrie du triangle. Ces méthodes, assez élémentaires, ne permettent pas d'aller beaucoup plus loin. Par exemple, démontrer l'existence d'une solution est hors de portée. Il faut attendre près de 2 000 ans pour que l'étude de cette question soit enrichie à l'aide d'apports théoriques de nature différente.

Jacques Bernoulli étudie la question pour répondre à des questions de mécanique statique et plus précisément s'intéresse à la forme que doit posséder une poutre pour offrir le maximum de résistance possible, la résolution d'une telle question débouche sur un théorème isopérimétrique, le demi-cercle est parfois la forme offrant la meilleure résistance. Si Bernoulli ne parvient pas à finaliser un résultat, il utilise de nouveaux outils issus du calcul différentiel. Le mariage de la géométrie et de l'analyse est promis à un grand avenir, même si un théorème isopérimétrique n'est pas encore accessible.

Le XIX^e siècle est celui des progrès majeurs. La première avancée est le fruit du travail de Jakob Steiner . Il montre que, si une solution existe, elle est nécessairement unique et c'est le disque. Pour cela, il développe un outil, maintenant appelé symétrisation de Steiner et encore utilisé pour établir des théorèmes d'isopérimétrie. Son idée majeure consiste à remarquer que, si l'on coupe une solution à l'aide d'une droite en deux parties de surfaces égales, il est possible de construire une nouvelle surface optimale à l'aide de la duplication d'une des deux parties. Sa démonstration est présentée dans l'article Isopérimétrie.

Calcul variationnel

Pour l'obtention d'une preuve complète, au moins en dimension 2, une difficulté majeure n'est toujours pas franchie, celle de la preuve de l'existence d'une solution. Les premiers éléments de réponse proviennent de la démarche initiée par Bernoulli. Une hypothèse supplémentaire, un peu étrange, est supposée : la frontière de la surface est lisse. L'étrangeté provient du fait qu'une ondulation sur la surface a tendance à plus augmenter le périmètre que l'aire. Plus la courbe frontière est irrégulière, plus elle est loin de l'optimale, mais plus la démonstration devient difficile. Karl Weierstrass formalise le calcul des variations et établit les bases de l'analyse fonctionnelle. Cette approche consiste à étudier non pas une courbe spécifique, mais un ensemble de courbes qui varient, par exemple à l'aide d'un paramètre. En faisant varier ces courbes, on montre que le cercle est l'optimum recherché. Au moins pour la dimension 2, une fois l'existence d'un optimum établi pour les surfaces à la frontière régulière, il n'est plus trop difficile de montrer le théorème général, on sait en effet approximer une courbe fermée continue par une autre continûment dérivable.

La généralisation aux dimensions supérieures est naturelle. Dans un premier temps, on suppose l'existence d'une solution au théorème et on montre que cette solution est nécessairement une sphère de dimension n. Le raisonnement est très physique, c'est celui qui détermine la forme d'une bulle de savon. L'équilibre de la bulle est le fruit de deux forces qui s'annulent : la pression due à l'aire enfermée dans la bulle et la tension superficielle de la surface. Un rapide calcul de variation montre que la courbure moyenne de la sphère est nécessairement constante. En 1900, on sait que le seul compact strictement convexe de courbure moyenne constante est une sphère. Une fois encore, la démonstration de l'existence d'une solution s'avère la partie délicate. Une première démonstration en dimension 3 est l'œuvre H. A. Schwarz en 1890.

Géométrie des convexes

Si la démarche fondée sur le calcul variationnel débouche, la généralisation à des dimensions supérieures n'est pas aisée. Une autre approche, issue de la théorie algébrique des nombres est finalement plus prometteuse. Hermann Minkowski développe une approche géométrique qui l'amène à étudier le nombre de points à coordonnées entières que contiennent certains convexes, problème proche de l'isopérimétrie. La fonction qui associe à un convexe compact de Rⁿ, le cardinal de son intersection avec le réseau Zⁿ est une mesure. Le théorème de Minkowski, qui procède de cette logique, permet d'élucider de manière élégante la structure du groupe des classes d'idéaux. Une nouvelle structure géométrique est étudiée ; au lieu de considérer une géométrie euclidienne de dimension n, Minkowski étudie un ensemble dont les points sont des compacts convexes. Cet ensemble est muni d'une addition.

Felix Hausdorff trouve une distance naturelle pour un espace un peu plus vaste, celui des compacts. La topologie associée à cette distance est bien adaptée. Les fonctions volumes et surfaces, qui associent à un convexe compact sa mesure et la mesure de sa frontières sont continues. Il en est de même pour la somme de Minkwoski. Enfin, l'espace est complet ainsi que le sous-ensemble des convexes. Enfin les polytopes forment un ensemble dense.

En dimension 2, l'étude de la somme de Minkwoski et de la sphère de rayon t et de centre le vecteur nul avec un convexe compact donne l'expression polynomiale a + pt + πt², où a désigne l'aire du convexe et p son périmètre. Démontrer le théorème isopérimétrique en dimension 2 revient à montrer que p² est plus grand que 4πa, ce qui revient à dire que l'expression polynomiale précédente admet des racines réelles, ce que fait Minkowski. T. Bonnesen va plus loin, en 1921 il démontre que si r est le rayon d'un cercle inscrit et R le rayon d'un cercle circonscrit, on dispose de la majoration suivante :

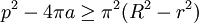
Autrement dit, l'égalité ne peut avoir lieu que si le convexe est un disque. Cette démarche peut être généralisée aux dimensions supérieures. A. Aleksandrov et W. Fenchel utilisent cette démarche pour établir le théorème isopérimétrique général, pour les géométries euclidiennes et la mesure de Lebesgue en 1937.