Théorème isopérimétrique - Définition

Dimension supérieure

Enoncé

Une bulle de savon est une réponse naturelle au théorème isopérimétrique en dimension 3. La tension superficielle de la bulle possède une énergie potentielle minimale si sa surface l'est. L'équilibre statique est obtenu quand la surface est minimale pour enserrer la quantité d'air enfermée dans la membrane de savon. La sphère est l'unique surface réalisant cet optimum, d'où la forme de la bulle. En dimension trois, on dispose du théorème suivant :

• Soit K un compact d'un plan euclidien de dimension 3 et dont la surface est mesurable. La boule de même surface que celle de la frontière de K possède un volume plus grand que celui de K. Si v est le volume de K et s sa surface, la majoration suivante, dite inégalité isopérimétrique est vérifiée :

De manière plus générale, si μ désigne la mesure de Lebesgue dans un espace euclidien de dimension n, μ_n-1 la mesure équivalente pour les sous-variétés de dimension n - 1 et si K est un compact mesurable de frontière aussi mesurable, alors :

Ici, B désigne la boule unité. Un rapide calcul permet de déduire de cette majoration les inégalités isopérimétriques pour n égal à 2 ou 3.

Difficultés

Certaines démonstrations, établies en dimension 2, se généralisent aisément aux dimensions quelconques. C'est, par exemple, le cas pour la formule de Leibniz donnant l'expression d'un déterminant. Un résultat faisant appel à la topologie est très souvent beaucoup plus complexe à établir. Un exemple célèbre est celui de la conjecture de Poincaré. Si le résultat équivalent en dimension 2 est relativement simple, en dimension 3 il s'avère redoutable à démontrer. Sans atteindre des extrêmes aussi techniques, démontrer le théorème isopérimétrique pour un espace euclidien de dimension quelconque est plus ardu qu'en dimension 2.

Une première difficulté, déjà citée, provient du fait qu'il n'existe pas de suite infinie de polygones réguliers convexes à partir de la dimension 3. Cependant, un contournement est aisément imaginable.

La géométrie des convexes diffère. A partir de la dimension 3, une enveloppe convexe d'un compact n'est pas nécessairement de frontière de mesure plus petite que la mesure de la frontière du compact. Un contre exemple est donné en dimension 3 par une variété analogue à la chambre à air d'un vélo. Son enveloppe convexe contient deux disques supplémentaires, dont l'aire peut être supérieure à celle de la moitié de la surface de la variété qui n'est pas à la frontière de l'enveloppe convexe.

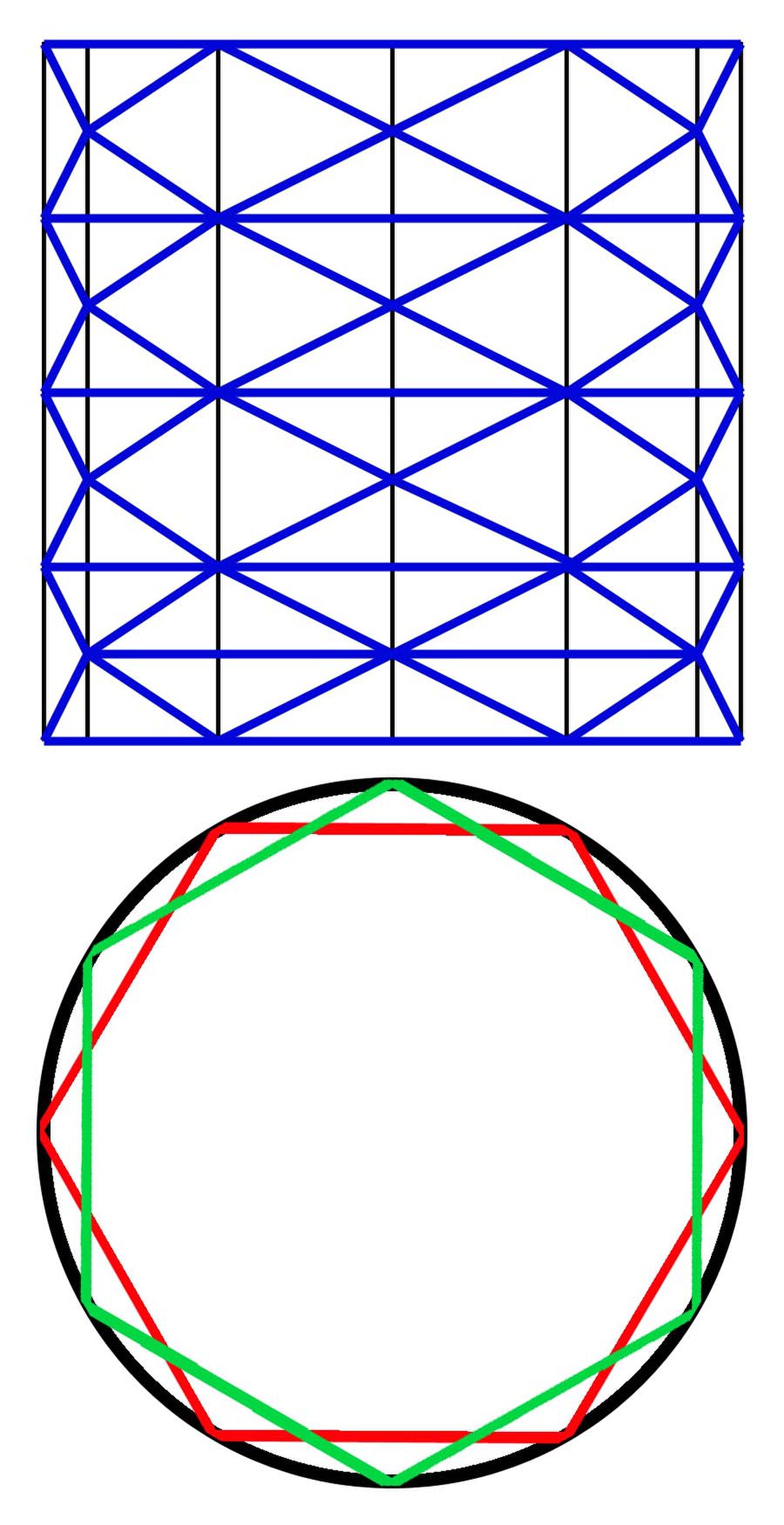
Enfin, le sens à donner au mot mesure de la frontière n'est pas aussi simple à partir de la dimension 3, que dans le plan. Dans le plan, définir la longueur d'une courbe est aisé avec l'approche de Jordan, on considère la borne supérieure de l'ensemble des lignes polygonales sont les sommets sont ordonnés et situés sur la courbe (cf l'article Longueur d'un arc). A partir de la dimension 3, cette démarche n'est plus possible, il existe des suites de polyèdres dont les points sont tous sur la surface d'une portion de cylindre située entre deux plans parallèles dont la suite des surfaces diverge. Un exemple est donné sur la figure de droite. La notion de forme volume permet bien de définir une mesure n - 1 dimensionnelle pour la frontière du compact, elle suppose cependant que la frontière est suffisamment lisse, c'est-à-dire qu'elle définisse une variété de dimension n - 1 de classe C².

Variété différentielle

Contenu de Minkowski

Pour obtenir une définition générale de la mesure de la frontière du compact étudié dans un espace euclidien E de dimension n, Minkowski définit la notion de contenu k dimensionnel, ici k désigne un entier plus petit que n. Soit D un compact fermé de E, son contenu k dimensionnel M_n-k(D) est le suivant :

Ici, B_p désigne la boule unité d'un espace euclidien de dimension p. En toute rigueur, on devrait parler de contenu k dimensionnel inférieur. La figure de droite illustre le concept pour la frontière d'un compact. La partie supérieure de la fraction définissant le contenu correspond au volume d'un tube de section un disque de rayon t si la figure est en dimension 3. Si la frontière est une variété de classe C₂, le volume du tube est égal à sa longueur que multiple la surface du disque de rayon t, si t n'est pas trop grand. Le rapport définissant le contenu est toujours égal à la longueur de la variété

Dans le cas plus général d'une variété compacte de dimension k et de classe C₂, le volume du tube s'exprime comme un polynôme de degré n - k dont le terme de plus petit degré est égal à la mesure de la variété. La mesure est alors définie à l'aide de la forme volume canonique. Ce résultat se conçoit bien intuitivement, l'intersection du tube en un point de la variété par l'espace affine orthogonal à la variété en ce point est une boule de dimension n - k et de rayon t. En première approximation, le volume du tube est le produit de la mesure de cette boule par celle de la variété.

Egalité isopérimétrique pour la boule

Le choix du contenu de Minkowski pour mesurer la frontière du compact considéré est pertinent. On peut s'en rendre compte par l'étude de l'égalité isopérimétrique dans le cas d'une boule r.B de rayon r d'un espace euclidien E de dimension n. Sa mesure est égale à :

Si la surface est désignée par la lettre S, on a :

La deuxième égalité indique que le tube engendré par la surface S_n-1 est composé des points de la boule de rayon r + t qui ne sont pas éléments de la boule r - t. Ce volume se calcule aisément :

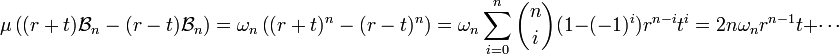
On en déduit :

Ce qui est bien l'égalité isopérimétrique.

Inégalité de Brunn-Minkowski

L'inégalité de Brunn-Minkowski permet aisément de démontrer l'inégalité isopérimétrique, dans le cas d'un compact non vide K. Appliquée à K et à t.B, on obtient :

Autrement dit :

Il suffit de remarquer que le terme de gauche admet pour limite inférieure le contenu n - 1 dimensionnel de la frontière de K. Ce résultat est connu sous le nom de formule de Steiner-Minkowski. On obtient :

Ce qui correspond bien à l'inégalité isopérimétrique. Aucune hypothèse n'a été faite sur la nature du compact K.

Inégalité d'Alexandrov-Fenchel

La démonstration est à la fois simple et rapide, mais il manque l'unicité de la solution. Des hypothèses supplémentaires permettent une démonstration plus simple de cette unicité. Le cas général ne peut s'exprimer aisément ; pour s'en rendre compte, il suffit de considérer une boule dans laquelle on plante une aiguille infiniment fine. Il existe deux cas où le théorème isopérimétrique s'exprime aisément. Dans le cas des convexes compacts, ou dans le cas des variétés à bord de classe C², l'unicité de l'optimum se démontre à l'aide de l'inégalité d'Alexandrov-Fenchel.