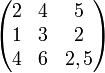Théorème du minimax de von Neumann - Définition
La liste des auteurs de cet article est disponible ici.
Le modèle économique sous-jacent



On suppose que deux protagonistes, Xavier et Yvette, s'affrontent dans un contexte qui peut être un « jeu », au sens commun du terme (ainsi le pierre-feuille-ciseaux), mais aussi une compétition militaire ou économique. On en trouvera deux exemples (des plus primaires) à l'article Jeu à somme nulle.
Chacun dispose d'un nombre fini de coups possibles, appelés des « stratégies pures ». On note « k » le nombre de stratégies pures disponibles pour Xavier et « n » le nombre de stratégies pures disponibles pour Yvette. On numérote de 1 à k les stratégies à la disposition de Xavier et de 1 à n celles d'Yvette. Dans l'exemple du jeu de pierre-feuille-ciseaux, le formalisme sera le même pour Xavier et pour Yvette : n = k = 3, « 1 » codant « jouer pierre », « 2 » codant « jouer feuille » et « 3 » codant « jouer ciseaux » (on prendra garde que cet exemple peut être trompeur : on ne suppose pas le jeu symétrique et les deux joueurs n'ont pas nécessairement les mêmes stratégies pures à leur disposition, ni même le même nombre de stratégies pures.)
On suppose que les deux joueurs connaissent sans ambiguïté la règle du jeu, en particulier les gains ou pertes qui seront applicables pour chaque couple de choix de stratégies (le jeu est dit « à information complète »), et qu'à chaque coup ils jouent simultanément (le jeu est dit « synchrone » — on peut aussi utiliser l'expression « jeu à information complète imparfaite » pour exprimer ce synchronisme). Il leur est interdit de se concerter préalablement : le jeu est dit « non coopératif ».
Pour chaque choix d'une stratégie pure numérotée « j » par Xavier et d'une stratégie pure numérotée « i » par Yvette, les règles du jeu (bien connues des deux participants) définissent un gain aij remporté par Xavier, qui est un nombre réel. Une valeur positive signifie que Xavier est bénéficiaire de ce nombre d'unités, un gain négatif qu'il en est perdant. Ces gains peuvent être regroupés en un tableau rectangulaire, appelé matrice (les lignes correspondant aux stratégies d'Yvette et les colonnes à celles de Xavier). Dans l'exemple de « pierre-feuille-ciseaux » avec ses règles les plus usuelles, la matrice A représentant les gains de Xavier serait ainsi :
| Xavier joue « pierre » | Xavier joue « feuille » | Xavier joue « ciseaux » | |
| Yvette joue « pierre » | 0 | 1 | -1 |
| Yvette joue « feuille » | -1 | 0 | 1 |
| Yvette joue « ciseaux » | 1 | -1 | 0 |
On pourrait définir de même le gain « bij » pour Yvette et la matrice représentant ces gains, mais ce ne sera pas nécessaire car on fait une dernière hypothèse : celle que le jeu est « à somme nulle », ce qui signifie que la société formée des deux joueurs ne gagne ni ne perd rien au jeu dans sa globalité, que tout ce que perd Xavier, Yvette le gagne et réciproquement. La matrice des gains d'Yvette est donc la matrice − A et il n'est pas utile de lui donner un nouveau nom.
Points-selles dans les matrices de gain
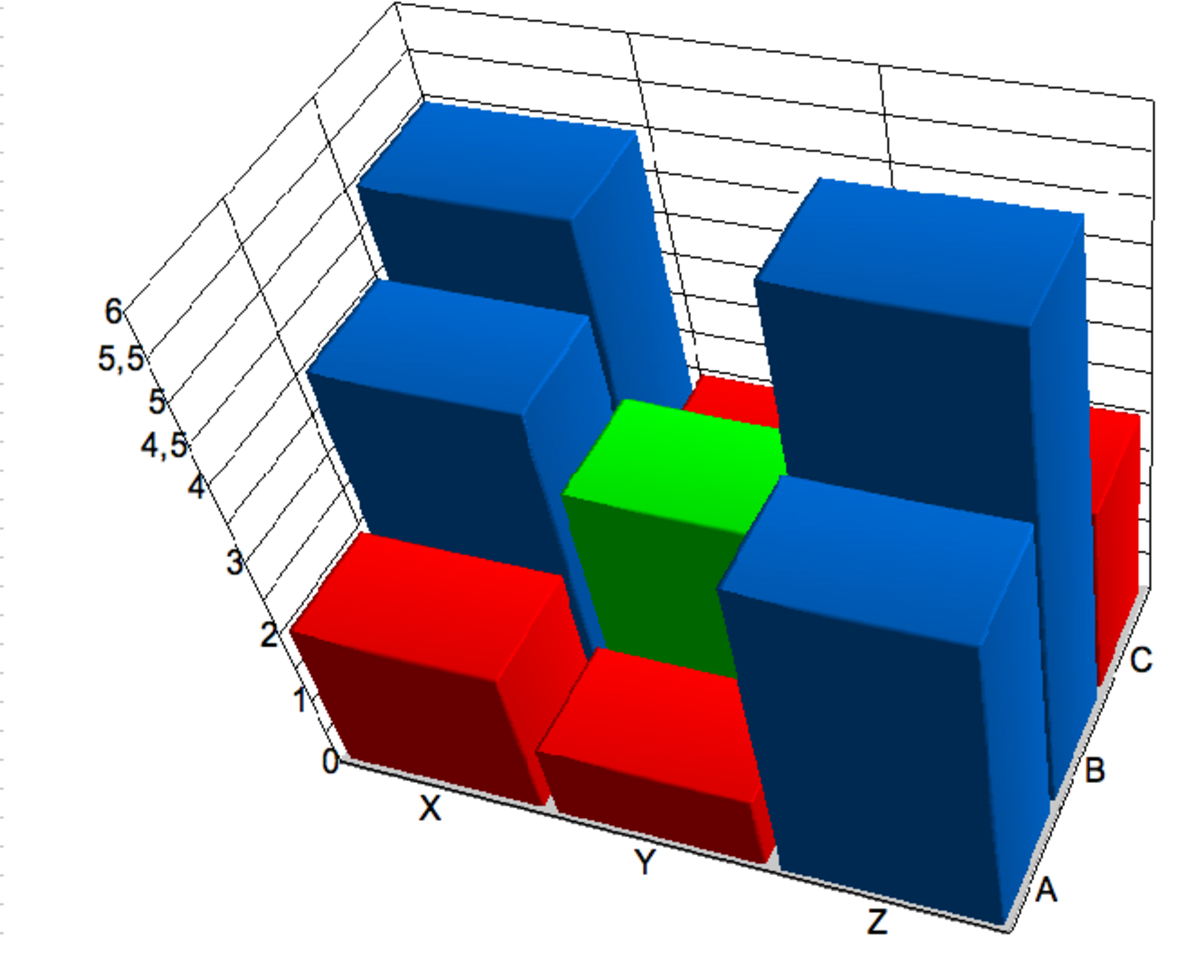
Soit l'exemple d'un jeu à trois stratégies pour chaque joueur où la matrice A des gains de Xavier est la suivante :
| Xavier joue sa stratégie 1 | Xavier joue sa stratégie 2 | Xavier joue sa stratégie 3 | |
| Yvette joue sa stratégie 1 | -1000 | 2 | 2000 |
| Yvette joue sa stratégie 2 | 1010 | 2 | -3000 |
| Yvette joue sa stratégie 3 | 0 | 1 | 0 |
Considérant la règle du jeu, Xavier se dit : « Si je joue 1, je risque de perdre 1000 unités, et si je joue 3 d'en perdre 3000 ; mais si je joue 2, je gagne une unité dans le pire des cas. »
Yvette, pour sa part, se dit : « Si je joue 1, je risque de perdre 2000 unités, et si je joue 2 d'en perdre 1010 ; mais si je joue 3 mes pertes sont limitées à une unité dans le pire des cas.
Xavier peut poursuivre son raisonnement : « J'ai reconstitué le raisonnement d'Yvette, qui lui donne de bonnes raisons de choisir sa stratégie 3. Si elle le fait comme je m'y attends, la lecture de la 3e ligne de la matrice me montre que la stratégie 2 est le meilleur choix pour moi. Excellente raison de m'y tenir. »
Et symétriquement, après avoir observé la 2e colonne de la matrice, Yvette se sent confortée dans son choix pour la stratégie 3.
Finalement tout ceci mène à penser que le choix conjoint du 2e coup pour Xavier, du 3e pour Yvette est plus rationnel que les autres, qu'il est le bon choix en un sens qui reste à préciser. Il est à cet égard instructif de considérer deux règles de décision inappropriées qui pourraient tenter Xavier : en premier lieu, il pourrait chercher à maximiser la moyenne d'une colonne, en l'interprétant comme le gain moyen que lui rapporterait le choix de la stratégie correspondante, et il jouerait alors son 1er coup ; en second lieu, il pourrait être attiré par le « maximax », le gain le plus élevé figurant sur le tableau (ici c'est 2000), ce qui le conduirait à jouer son 3e coup. Dans les deux cas, il y perdrait, puisqu'Yvette — si elle joue bien — s'en tiendrait tout de même à jouer son coup numéro 3 et le seul résultat de la gourmandise de Xavier serait qu'il ne toucherait rien au lieu de gagner le modeste 1 que la meilleure stratégie lui garantit.
Comparons à la situation suivante, variante minime du jeu de « pierre-feuille-ciseaux » (on a modifié de quelques centimes les enjeux pour éviter des situations d'indifférence entre stratégies qui n'apportent rien à la compréhension) :
| Xavier joue « pierre » | Xavier joue « feuille » | Xavier joue « ciseaux » | |
| Yvette joue « pierre » | 0 | 1,05 | -1,07 |
| Yvette joue « feuille » | -1,03 | 0 | 1,04 |
| Yvette joue « ciseaux » | 1,02 | -1,01 | 0 |
Xavier et Yvette peuvent commencer à raisonner comme dans l'exemple précédent : si Xavier veut minimiser la somme qu'il devra verser à Yvette, le coup à jouer est « feuille » où il ne perdra au pire que 1,01 unité. De même Yvette va dans un premier temps être tentée par jouer « ciseaux » où dans le pire des cas sa perte se limite à 1,02 unité. Mais lorsqu'il considère qu'Yvette a des raisons sérieuses de jouer « ciseaux » Xavier, au lieu d'être conforté dans son choix initial de « feuille », s'aperçoit qu'il serait alors perdant et qu'il vaut mieux bien mieux bifurquer sur « pierre ». Yvette, qui reconstitue mentalement les anticipations de Xavier, anticipe qu'il jouera « pierre » et déplace son projet de coup vers « feuille ». À son tour Xavier modifie ses anticipations... Rien ne se stabilise et aucun choix de stratégies pures n'arrive à s'imposer.
Où se situe la différence entre les deux exemples ? C'est que dans la première matrice, contrairement à la deuxième, figure ce qu'on peut appeler un point-selle, ou équilibre de Nash : une entrée qui est à la fois la plus petite de sa colonne et la plus grande de sa ligne.
Proposition : Les points-selles étant définis comme ci-dessus, une matrice (n,k) de réels A = (aij) possède un point-selle si et seulement si
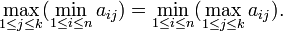
En tout point-selle de la matrice, l'entrée correspondante du tableau est égale à ce minimax.
- Supposons l'égalité du minimax et du maximin, et montrons l'existence d'un point-selle.
Notons i0 un indice pour lequel
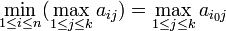
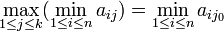
Vu l'hypothèse d'égalité du maximin et du minimax, on en déduit l'égalité :
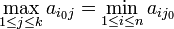
On va vérifier que la position (i0,j0) correspond à un point-selle. Soit (i1,j0) une autre position dans la même colonne. On écrit :
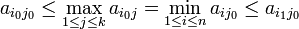
- Remarquons préalablement que l'inégalité
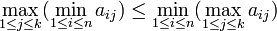
est vérifiée pour n'importe quelle matrice A, qu'elle contienne ou non des points-selles.
Soit en effet i0 un indice pour lequel
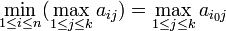
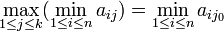
Comme
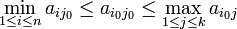
- Supposons qu'une position (i0,j0) corresponde à un point-selle.
Alors par définition d'un point-selle,
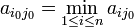
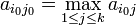
On en déduit que
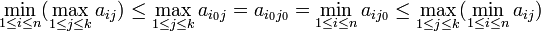
Voyons comment s'applique cette proposition sur les exemples :
pour le premier exemple,
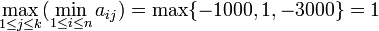
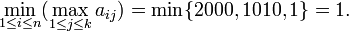
Dans le second cas,
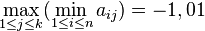
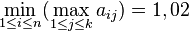
Signification intuitive du maximin
L'expression
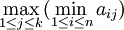
Pour un j donné, l'expression
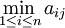
Quand ensuite Xavier considère le max de ces min (le « maximin ») il détermine, parmi les k coups qui lui sont proposés, celui qui a pour lui les résultats les moins fâcheux dans l'optique pessimiste où Yvette, infiniment chanceuse ou psychologue, déjoue forcément le choix stratégique de Xavier. Choisir le maximin pour lui, c'est donc choisir la solution la moins risquée en mesurant le risque de chacune par la seule considération de l'hypothèse la plus défavorable.
Dans son exposé de la théorie des jeux pour un large public, William Poundstone synthétise élégamment cette explication en citant Italo Calvino : « Tu sais que ce que tu peux espérer de mieux est d'éviter le pire ».
Stratégies mixtes
On peut aller plus loin à condition d'imaginer une extension de la notion de stratégie. Jusqu'à présent, chaque joueur n'avait le choix qu'entre des « stratégies pures » : il pouvait décider quel coup jouer. On lui offre désormais une nouvelle possibilité : choisir judicieusement une mesure de probabilité sur l'ensemble fini des stratégies pures, puis jouer aléatoirement en pondérant son tirage par la mesure préalablement choisie. On appellera ainsi stratégie mixte une probabilité sur l'ensemble fini des stratégies pures accessibles à un joueur.
Une mesure de probabilité P sur l'ensemble fini
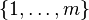
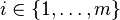
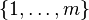
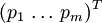
Dans l'exemple du jeu pierre-feuille-ciseaux, choisir la stratégie mixte
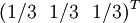
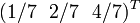
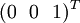
Pour chaque choix d'une stratégie mixte
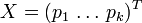
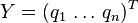
L'espérance de gain pour Xavier sous l'hypothèse de choix de ces deux stratégies mixtes se calcule alors comme une espérance mathématique : c'est
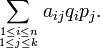
Il s'agit de l'unique terme de la matrice YTAX, qui est de taille (1,1) ; et cette dernière s'interprète donc comme le gain que peut attendre Xavier, en moyenne, lorsque les stratégies mixtes choisies sont X et Y.
Il est alors possible de définir la notion d'équilibre de Nash pour cette fonction de gain comme on a défini les points-selles plus haut : on dira qu'un couple de stratégies mixtes
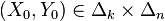
- d'une part, pour tout
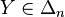
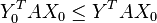
- d'autre part, pour tout
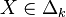
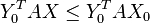
Comme avec le modèle qui ne connaît que les stratégies pures, lorsqu'il existe un équilibre de Nash on peut exposer des arguments heuristiques justifiant que celui-ci constitue un choix raisonnable pour les deux joueurs ; comme plus haut, son existence est caractérisée par une propriété de minimax et on montre la
Proposition : Soit A = (aij) une matrice (n,k) de réels. Il y a un équilibre de Nash pour A (au sens défini ci-dessus) si et seulement si
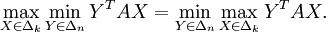
En tout équilibre de Nash (X0,Y0) pour A, la valeur de
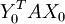
Le maximin qui apparaît dans ce calcul matriciel s'interprète comme celui de la situation à point-selle, la nouveauté étant que les ensembles de choix sont désormais infinis. Pour chaque stratégie mixte envisageable, Xavier soupèse quelle conséquence elle aurait pour lui dans une hypothèse pessimiste (c'est
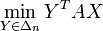
Ce qu'affirme alors le théorème du minimax de von Neumann, c'est l'existence d'un tel équilibre de Nash pour toute matrice A. Ce résultat reste d'ailleurs vrai sans l'hypothèse de « somme nulle », comme l'a montré John Forbes Nash en 1949, mais n'est alors plus lié à une propriété de minimax.
Retour aux exemples
Voyons sur les deux exemples étudiés plus haut quelles répartitions de probabilité constituent l'équilibre de von Neumann.
Dans le jeu avec point-selle, on peut s'attendre à ce que ce soient sur des stratégies pures, et c'est en effet le cas : notons
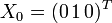
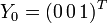
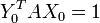
Considérons un autre
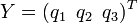
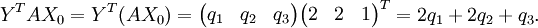
Comme par hypothèse
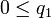
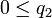
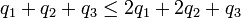
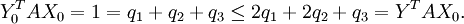
La première condition définissant les équilibres de Nash est bien vérifiée. La vérification de la seconde n'est pas plus difficile. L'équilibre de Nash est identifié, et reste composé de stratégies pures même dans l'extension du modèle à des stratégies probabilistes.
Examinons maintenant l'exemple du jeu pierre-feuille-ciseaux, cette fois-ci sous sa forme la plus simple avec la matrice de gain
| Xavier joue « pierre » | Xavier joue « feuille » | Xavier joue « ciseaux » | |
| Yvette joue « pierre » | 0 | 1 | -1 |
| Yvette joue « feuille » | -1 | 0 | 1 |
| Yvette joue « ciseaux » | 1 | -1 | 0 |
qui est dépourvue de point-selle.
On essaie ici conformément à l'intuition
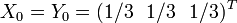
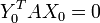
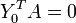
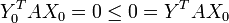
Critiques du modèle
Le modèle économique utilisé ne peut se contenter d'un concept d'utilité ordinale. Si on se borne à supposer comparables entre elles les satisfactions ou désagréments d'un joueur, on construit un ensemble totalement ordonné : on peut ainsi dire que Xavier préfère gagner 100 euros à ne rien gagner du tout, et ne rien gagner du tout à perdre 100 euros. Mais que fera-t-il si on lui propose de participer à une loterie où il a une chance sur deux de s'enrichir de 100 euros et une chance sur deux de s'appauvrir du même montant ? Est-ce pour lui plus tentant que de s'abstenir et de s'assurer ainsi de ne rien perdre, mais ne rien gagner non plus ? Si le joueur ressent de l'aversion pour la prise de risque, il refusera la loterie puisqu'elle lui propose le même gain moyen que l'abstention, mais avec plus de risque. Mais comment maintenant se comportera-t-il si on lui offre deux chances sur trois de gagner et une chance sur trois de perdre ? À partir de quelle valeur du paramètre accepte-t-il de jouer ? L'introduction d'une théorie cardinale de l'utilité permettrait de répondre, une théorie purement ordinale ne suffit pas en revanche à donner un sens à une espérance de gain en situation aléatoire, et donc à mettre sur pied le modèle justifiant les applications en économie du théorème du minimax.
Pour donner un sens au calcul d'espérance mathématique par lequel passe la justification du modèle, von Neumann et Morgenstern se sont efforcés de fonder l'utilisation d'une théorie cardinale, et ont développé une théorie de l'utilité de l'incertain suffisante pour fonder leur modèle. Mathématiquement rigoureuse, la théorie n'en a pas moins été contestée dès son introduction, la contestation passant nécessairement par celle de ses axiomes : voir en ce sens le fameux paradoxe d'Allais, explicité par Maurice Allais.
Mais si l'utilité cardinale n'est qu'un concept mathématique découplé de la réalité, les formalisations probabilistes en théorie des jeux sont mal fondées. Tout en nuançant son propos (il concède que les théories de la décision qu'il critique « ont établi leur pertinence et leur puissance dans de multiples applications »), Russel Hardin peut ainsi décocher quelques flèches contre les modèles à base de stratégies mixtes : il fait par exemple observer qu'il se pourrait bien qu'il n'y ait aucun moyen sensé de définir une combinaison de victoires et de défaites de deux pays en guerre qui puisse être raisonnablement considérée comme à mi-chemin de la victoire totale et de la défaite totale d'une des parties.
Enfin, même en admettant pouvoir définir pour chaque joueur une utilité cardinale et donc développer une théorie considérant des stratégies mixtes, cela ne suffit pas à justifier qu'on puisse reconnaître si un jeu vérifie l'hypothèse de « somme nulle » : pour pouvoir exiger que le gain de Xavier équilibre la perte d'Yvette, il faut aussi postuler la comparabilité de leurs utilités, ce qui ne va pas de soi.