Théorème des deux carrés de Fermat - Définition

Introduction

Pierre Fermat

En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c'est-à-dire de deux carrés d’entiers) et précise de combien de façons différentes il peut l’être. Par exemple, selon ce théorème, un nombre premier impair est une somme de deux carrés parfaits si et seulement si le reste de sa division euclidienne par 4 est 1 ; dans ce cas, les carrés sont déterminés de manière unique. On peut le vérifier sur 17 (= 4x4 + 1) ou 97 (= 24x4 + 1), qui sont bien tous deux d’une seule façon une somme de deux carrés (17 =1²+4² et 97 = 9²+4²), alors que des nombres premiers comme 7 (=4x1+3) ou 31 (4x7+3) ne sont pas des sommes de deux carrés. Ce résultat est parfois nommé simplement théorème des deux carrés ou bien encore théorème de Fermat de Noël.

Il s’inscrit dans la longue histoire de la représentation de nombres comme sommes de carrés qui remonte à l’Antiquité. Il est explicité par Pierre de Fermat au XVII^e siècle, mais la première preuve publiée connue est l'œuvre de Leonhard Euler un siècle plus tard. Sa démonstration ne clôt pas les interrogations. Des nouvelles preuves et diverses généralisations sont proposées au cours des siècles suivants. Elles ont joué un rôle important dans le développement d’une branche des mathématiques appelée théorie algébrique des nombres.

À l'instar de beaucoup d'équations diophantiennes, c’est-à-dire d’équations dont les coefficients et les solutions cherchées sont des nombres entiers ou fractionnaires, la simplicité de l'énoncé cache une difficulté réelle de démonstration. Certaines des preuves proposées ont aidé à la mise au point d'outils parfois sophistiqués, comme les courbes elliptiques ou la géométrie des nombres, liant ainsi la théorie des nombres élémentaire à d’autres branches des mathématiques.

Présentation du théorème

Le cas des nombres premiers

Certains nombres premiers sont sommes de deux carrés parfaits. C’est bien sûr le cas de 2 (=1² + 1²), de même, 5 est la somme de 1 et de 4. D'autres comme 3 ou 7 ne vérifient pas cette propriété. Un test systématique jusqu'à 40 montre que :

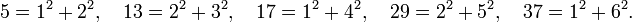
En revanche, 3, 7, 11, 19, 23 et 31 ne se décomposent pas ainsi. Le théorème fournit un critère général permettant de discriminer ces deux situations :

Théorème des deux carrés de Fermat (cas des nombres premiers) — Soit p un nombre premier impair, p est somme de deux carrés d'entiers naturels si et seulement si p est congru à 1 modulo 4 :

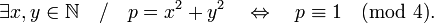
De plus, cette décomposition, quand elle existe, est unique, à l’échange près de x² et y².

Dire que "p est congru à 1 modulo 4" signifie simplement que le reste de la division euclidienne de p par 4 est 1, ou encore que le nombre p est de la forme 4k+1. Ce vocabulaire est explicité dans l'article Congruence sur les entiers.

Le cas général

Si, dans un premier temps, les entiers inférieurs à 50 sont écrits sur quatre lignes, en fonction du reste de leur division par quatre, on obtient :

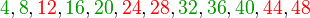
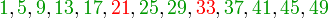
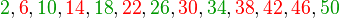
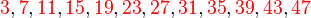
Les entiers notés en vert sont ceux qui peuvent s'écrire comme la somme de deux carrés parfaits, les entiers pour lesquels une telle écriture est impossible sont notés en rouge. On constate que la quatrième ligne ne contient pas de solution. Or le produit d'un nombre pair de facteurs de la forme 4k+3 est de la forme 4k+1, donc cette dernière ligne ne contient que des nombres qui ont un nombre impair de facteurs premiers de la forme 4k+3. Ceci donne une piste pour comprendre la situation générale.

Le cas d'un nombre n quelconque dépend de ses facteurs premiers. On a :

Ainsi 30 n’est pas somme de carrés, car 30 = 2.3.5, 3 intervient avec un exposant 1 dans sa factorisation en facteurs premiers. En revanche, 45 = 3².5 est somme de carrés, car 3 intervient à la puissance 2 (on trouve bien que 45 = 6² + 3²).

La question du nombre de couples de carrés dont la somme est égale à un entier n donné, est aussi plus difficile, ce nombre dépend des exposants des facteurs de n de la forme 4k+1. En écrivant , où n' est divisible seulement par 2 et des facteurs premiers de la forme 4k+3, et où les différents p_i sont les facteurs premiers de la forme 4k+1, alors n a 1/2(a+1)(b+1)(c+1)... décompositions différentes en somme de deux carrés si un au moins des exposants a, b, c, ... est impair et 1/2(a+1)(b+1)(c+1)...+1/2 décompositions si tous les exposants sont pairs.

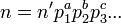
Une autre expression équivalente de ce nombre de décompositions a été donnée par Charles Gustave Jacob Jacobi  :

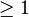
On compte toutes les représentations, même celles qui ne diffèrent que par le signe ou l'ordre. Par exemple, admet 8 représentations comme somme de deux carrés. On trouve cet énoncé et une preuve dans Introduction à la théorie des nombres de Hardy & Wright, théorème 278.

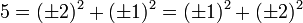
Un dernier aspect important est la construction explicite des carrés dont la somme est égale à un entier n donné.