Théorème des deux carrés de Fermat - Définition
La liste des auteurs de cet article est disponible ici.
Démonstrations
Les différentes démonstrations sont regroupées en fonctions des époques et des auteurs. En revanche, la rédaction choisie utilise le formalisme moderne : ainsi, la présentation des résultats de Diophante est très éloignée de la forme géométrique présente dans les textes originaux. Les preuves ont été choisies pour leur simplicité. En conséquence, la démonstration fondée sur les entiers de Gauss est due à Dedekind, celle utilisant les résultats de Lagrange sur les formes quadratiques est due à Gauss et certains résultats de Fermat sont exprimés en termes de résidus, vocable contemporain qui n'apparait qu'à la fin du XVIIIe siècle.
Époque de Diophante
Une première approche élémentaire montre que :
-
- Si un entier n est somme de deux carrés, alors le reste de la division de n par 4 n'est jamais égal à 3.
Elle se démontre en étudiant les restes de la division euclidienne par 4 d'un carré parfait.
Une identité remarquable due à Diophante (Arithmetica, III, 19), souvent dénommée identité de Brahmagupta permet d'établir le résultat suivant :
-
- Si deux entiers n et m sont sommes de deux carrés, alors leur produit est aussi somme de deux carrés.
Les deux entiers n et m peuvent être vus comme le carré du module de deux nombres complexes à parties réelle et imaginaire entières. Comme le produit de deux modules est égal au module du produit, il suffit de considérer les parties réelles et imaginaires du produit pour conclure.
Il est aussi possible d'établir directement l'identité sans référence aux nombres complexes :
-
- Si un entier n est somme de deux carrés, alors le reste de la division de n par 4 n'est jamais égal à 3.
Cette propriété provient du fait que la division d'un carré par 4 ne peut donner pour reste qu'une des deux valeurs 0 ou 1. En effet, soit a un entier :
- S'il est pair, il existe un entier m tel que a est égal à 2.m. Le carré de a est égal à 4.m2 qui est un multiple de 4, le reste de la division par 4 est égal à 0.
- S'il est impair, il existe un entier m tel que a est égal à 2.m + 1. L'identité remarquable ci-dessous montre que son carré est la somme d'un multiple de 4 et de 1, le reste de la division par 4 est égal à 1.
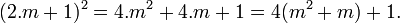
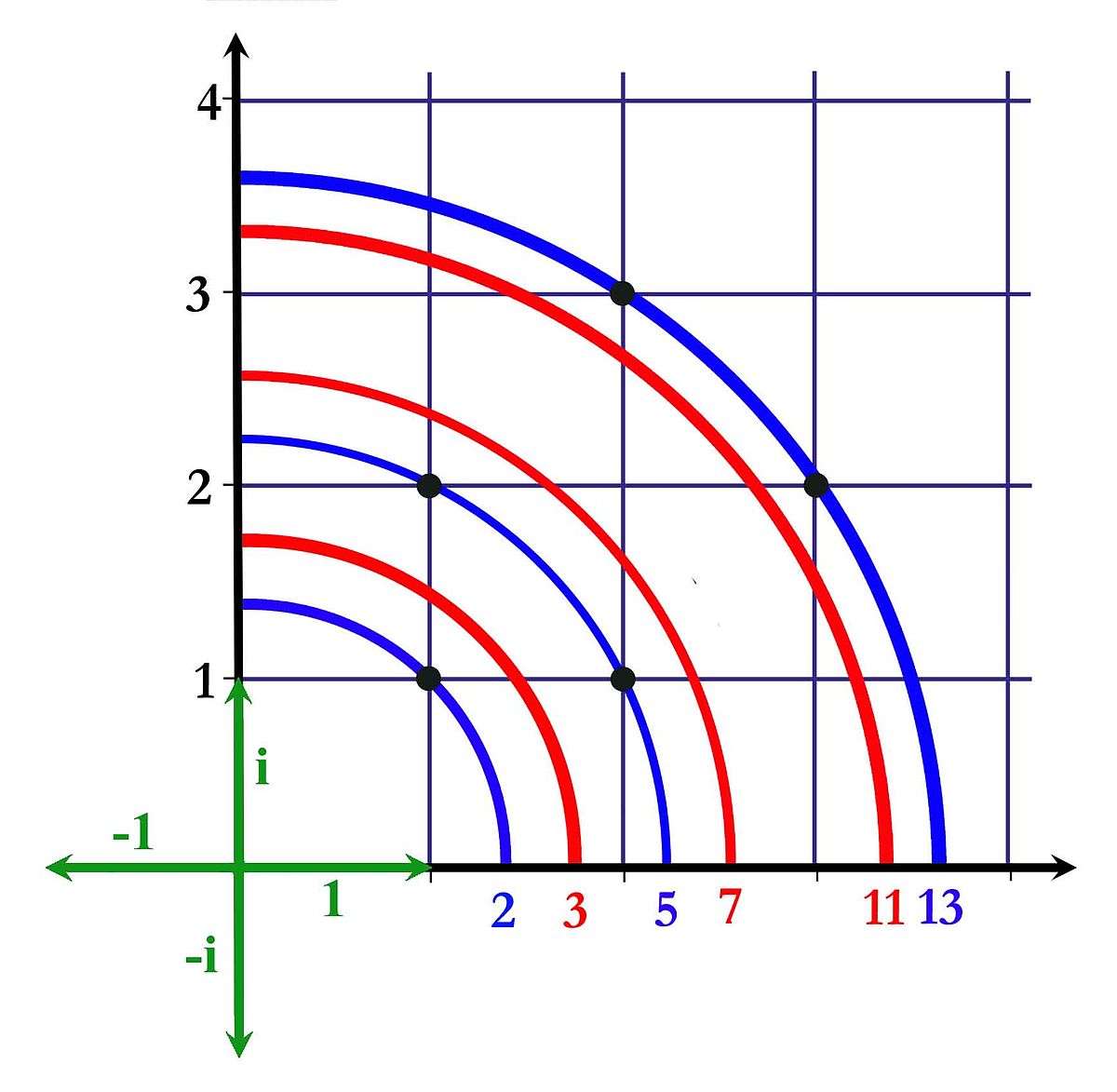
Si n est somme de deux carrés, notée n = a2 + b2, trois cas se présentent : a et b sont pairs, leurs carrés sont des multiples de 4 et leur somme est aussi un multiple de 4, l'un des deux est impair et l'autre pair alors la somme des carrés est la somme de deux multiples de 4 et de 1 et la division de la somme donne pour reste 1, enfin ils sont tous deux impairs et la somme des carrés est égal à la somme de deux multiples de 4 et de 2. Aucune configuration ne donne pour reste 3.
-
- Si deux entiers n et m sont sommes de deux carrés, alors leur produit est aussi somme de deux carrés.
Comme n et m sont sommes de deux carrés il existe quatre entiers a, b, c et d tel que les égalités suivantes soient vérifiées :
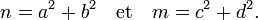
Cette proposition est la conséquence de l'identité de Diophante, qui s'énonce de la façon suivante :
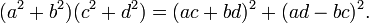
Pour s'en convaincre, il suffit de développer, puis factoriser le terme de droite :
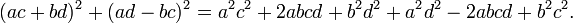
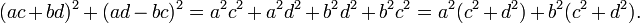
Une nouvelle factorisation montre l'égalité recherchée :
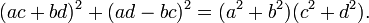
Conséquences de l'identité de Diophante
L'identité de Diophante permet d'aller plus loin dans l'analyse de l'équation. Elle permet de montrer que:
-
- Si un nombre premier p est somme de deux carrés, alors les deux carrés sont uniques.
Une autre propriété est utile :
-
- Si un entier n, somme de deux carrés, est divisible par un nombre premier m, somme de deux carrés, alors le quotient est lui-même somme de deux carrés.
La démonstration est de même nature que la précédente, elle est fondée sur des calculs algébriques astucieux utilisant la même identité. Ce résultat peut être utilisé pour établir une preuve du théorème. Il permet d'avancer aussi l'analyse du cas général. Il permet par exemple de démontrer la proposition suivante, présente dans une des preuves du théorème :
-
- Si un nombre n, somme de deux carrés, est divisible par un nombre m, qui n'est pas somme de deux carrés, alors le quotient q contient un facteur premier qui n'est pas somme de deux carrés.
-
- Si un nombre premier p est somme de deux carrés, alors les deux carrés sont uniques :
En effet, soit a2 + b2 et c2 + d2 deux sommes de deux carrés égal à p. On suppose ici que a, b, c et d sont quatre entiers positifs. Ils sont même strictement positifs, car si tel n'était pas le cas p serait un carré parfait, ce qui est impossible pour un nombre premier.
Montrons que p divise a.d - b.c et a.d + b.c. Pour cela, le calcul suivant est utile :
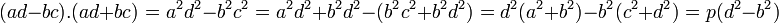
Le nombre premier p divise le produit de ad - bc par ad + bc. Le lemme d'Euclide montre que p divise l'un des deux facteurs. Si ad - bc est divisé par p, c'est-à-dire s'il existe un entier k1 tel que ad - bc = k1.p, on procède de la manière suivante. L'identité de Brahmagupta indique que :
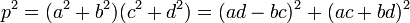
Ce qui montre que ac + bd est aussi un multiple de p et il existe un entier k2 tel que ac + bd = k2.p. L'égalité précédente s'écrit p2 = k12.p2 + k22.p2, et donc k12 + k22 est égal à un. Comme k1 et k2 sont deux entiers, l'un est nul l'autre est en valeur absolue égal à un. Il suffit de remarquer que ac + bd est strictement positif, car somme de produits de terme strictement positifs, pour conclure que k1 est nul, et ad - bc est aussi nul. Les deux vecteurs (a, b) et (c, d) sont proportionnels, ce qui montre l'existence d'un entier λ strictement positif tel que c = λ.a et d = λ.b. On en déduit que la somme c2 + d2 est égal à λ2.p et donc que λ est égal à un.
Si ad + bc est un multiple de p, l'égalité suivante montre que ac - bd est aussi un multiple de p :
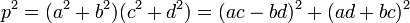
Le raisonnement précédent s'applique encore, il montre cette fois que a est égal à d et b à c. Les carrés sont identiques mais l'ordre est inversé.
-
- Si un entier n, somme de deux carrés, est divisible par un nombre premier m, somme de deux carrés, alors le quotient est lui-même somme de deux carrés :
Notons n = a2 + b2 et m = p2 + q2. Le raisonnement est analogue au précédent. Si n est divisible par le nombre premier m. Alors m divise le produit suivant :
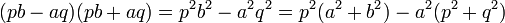
L'entier m est un nombre premier, le lemme d'Euclide indique qu'il divise l'un des deux facteurs, par exemple p.b - a.q. Comme lors de la démonstration précédente, l' identité de Brahmagupta montre que :
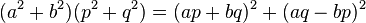
Ainsi, m divise (a.p + b.q)2, l'équation peut donc être divisée par le carré de m :
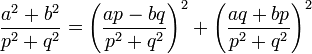
Ce qui démontre la proposition.
Si m2 divise p.b + a.q, un argument de même nature peut être utilisé avec :
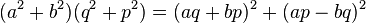
-
- Si un nombre n, somme de deux carrés, est divisible par un nombre m, qui n'est pas somme de deux carrés, alors le quotient q contient un facteur qui n'est pas somme de deux carrés.
Notons q = q1.q2. ... .qk, la décomposition du quotient en facteurs premiers. Alors n = m.q1.q2. ... .qk. Si chaque facteur qi est somme de deux carrés, la proposition précédente montre qu'il est possible de diviser n successivement par chaque qi et d'obtenir chaque fois un entier somme de deux carrés. Ce raisonnement montre que m est alors somme de deux carrés. La contraposée montre que si m n'est pas somme de deux carrés, alors au moins un qi n'est pas somme de deux carrés.
Fermat et les résidus
Une autre étape de la démonstration consiste à étudier les restes de la division euclidienne par p de chacun des termes de l'équation x2 + y2 = p. Comme le reste du terme de droite est nul, celui du terme de gauche est aussi nul. Cette démarche revient finalement à trouver une solution à l'équation suivante :
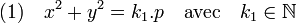
L'objectif est de trouver les solutions telles que ni x ni y ne soient des multiples de p. Comme p est premier, cela signifie que y et p sont premiers entre eux. L'identité de Bézout montre l'existence d'entiers α et β tels que :
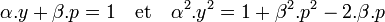
En multipliant par α2 l'équation (1) et en remplaçant α2.y2 par la valeur calculée précédemment, on obtient :
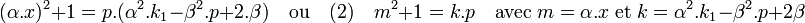
L'équation (2) admet toujours une solution si p est somme de deux carrés. Elle correspond à une simplification de l'équation générale, maintenant connue sous le nom du problème du résidu quadratique. Elle revient à déterminer dans quel cas un multiple d'un nombre premier s'écrit comme la somme d'un carré parfait et de un. Si p est un nombre premier différent de deux, la solution est donnée par la proposition suivante :
-
- Il existe un multiple de p s'écrivant comme somme d'un carré parfait et de un si et seulement si le reste de la division euclidienne de p par quatre donne pour reste un.
La condition est nécessaire, il a en effet déjà été démontré que le reste de la division euclidienne de m2 + 1 n'est jamais égal à trois. De nombreuses approches permettent d'établir la condition suffisante. L'une utilise le petit théorème de Fermat. Une connaissance plus avancée en arithmétique modulaire permet une démonstration plus expéditive.
-
- Démonstration à base d'arithmétique modulaire :
La question revient à montrer que la classe de -1 est un carré dans le corps Z/pZ si p - 1 est égal à 4.n, avec n un entier strictement positif. Le groupe multiplicatif de (Z/pZ)* est un groupe cyclique comptant 4.n éléments. Soit g un générateur de ce groupe. L'élément -1 est l'unique élément du groupe différent de l'unité et dont le carré est égal à l'unité. Cet élément est égal à g2.n, il est effectivement différent de l'unité, sinon g ne serait pas un générateur et le théorème de Lagrange, équivalent du petit théorème de Fermat avec ce formalisme, montre que son carré est égal à un. La valeur gn est donc un élément du groupe multiplicatif dont le carré est égal à -1.
-
- Démonstration sans arithmétique modulaire :
Ici, n désigne encore l'entier tel que p = 4.n + 1. Le petit théorème de Fermat montre que si x est un entier, alors x4n - 1 = (x2n - 1).(x2n + 1) est un multiple de p. Comme p est premier, l'un des deux facteurs de l'égalité est un multiple de p. Il suffit de trouver un entier a tel que a2n - 1 n'est un multiple de p, alors a2n + 1 l'est nécessairement et an est la solution recherchée.
Considérons la suite de polynômes Pn[X] définie par récurrence de la manière suivante :
![P_0[X] = X^{2.n} - 1 \quad \text{et}\quad P_{i+1}[X] = P_i[X + 1] - P_i[X]](https://static.techno-science.net/illustration/Definitions/autres/0/0f3249cb9b59893f1e75114d1c8027e0_a5c6d3846336259399bd72129e587292.png)
On remarque que si i est un entier compris entre 1 et 2.n, alors Pi[X] est un polynôme de degré 2.n - i et de monôme dominant ayant un coefficient égal au produit (2.n).(2.n - 1). ... .(2.n - i + 1 ). On en déduit que P2.n[X] est un polynôme constant égal à (2.n)! (ici le symbole ! désigne la fonction factorielle). Comme p est premier et supérieur à 2n, il n'est pas diviseur de (2.n)!. Or, P2.n[X], est combinaison linéaire à coefficients dans Z (l'ensemble des entiers), de valeurs que prend le polynôme P0[X] sur les entiers. Une de ces valeurs, notée a n'est donc pas un multiple de p. Comme P0[a] n'est pas un multiple de p, a2.n + 1 l'est, ce qui termine la démonstration.
Euler et la descente infinie
La démonstration d'Euler, présentée ici, suit exactement le plan indiqué par Fermat. Après l'utilisation du petit théorème de Fermat pour l'étude du résidu quadratique, il utilise la méthode de descente infinie. Cette méthode, souvent utilisée en arithmétique, se fonde sur les propriétés des entiers positifs. Elle propose des raisonnements par l'absurde fondée sur le fait qu'il n'existe pas dans N (l'ensemble des entiers positifs) de suite infinie strictement décroissante. La preuve consiste, à l'aide des hypothèses, à construire une suite infinie strictement décroissante d'entiers positifs. Comme une telle suite n'existe pas, il est démontré qu'une hypothèse est fausse.
Les démonstrations de cette nature s'appliquent plus naturellement pour l'obtention de propriété d'inexistence de solutions. Fermat l'utilise en particulier pour montrer une proposition équivalente à celle de son grand théorème pour n égal à quatre. La difficulté ici consiste à appliquer cette méthode pour démontrer un résultat positif : l'existence de solution. Euler trouve une méthode astucieuse, il établit d'abord le lemme suivant en utilisant la descente infinie :
-
- Si un entier n est somme de deux carrés parfaits n = a2 + b2 et si a et b sont premiers entre eux, alors chaque facteur premier de n est somme de deux carrés.
Une fois ce résultat établi, la démonstration est brève. Le paragraphe précédent montre qu'il existe un entier k tel que k.p soit somme de deux carrés m2 + 12 . Les deux entiers m et 1 sont premiers entre eux car 1 est premier avec tous les entiers. Le facteur p est donc, d'après la proposition précédente, somme de deux carrés.
On raisonne par l'absurde. On suppose qu'il existe un entier strictement positif n0 somme de deux carrés a2 + b2 et contenant un facteur premier qui ne soit pas somme de deux carrés. On suppose de plus que a et b sont premiers entre eux et quitte à intervertir les notations, on choisit a supérieur ou égal à b. L'entier n0 contient au moins deux facteurs premiers qui ne sont pas somme de deux carrés, car n0 est somme de deux carrés (cf la troisième proposition du paragraphe Conséquences de l'identité de Brahmagupta). Notons p le plus petit des deux et q l'entier tel que p.q soit égal à n0. L'entier q est plus grand que p car il contient un facteur au moins égal à lui.
L'objectif est construire un entier n1 strictement plus petit que n0, strictement positif et possédant les mêmes propriétés. Remarquons que :
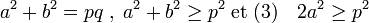
Soit α1 (resp. α2) les entiers positifs et r1 (resp. r2) les entiers en valeur absolue inférieur à la moitié de p tel que :
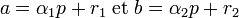
En remplaçant a et b par leurs valeurs, on obtient :
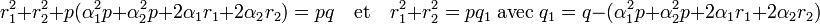
L'objectif est de montrer que q est strictement plus grand que q1. On remarque que :
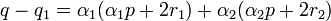
Les définitions de r1 et r2 montrent que la différence est toujours positive. La majoration (3) montre que α1 est strictement positif, le terme α1(α1 + 2r1) n'est nul que si p est égal à -2r1 et α1 est égal à un. Dans ce cas p est égal à 2.a. Cette configuration est impossible car alors a et b ne peuvent être premiers entre eux. La différence est donc toujours strictement positive.
Une propriété n'est pas encore assurée. Rien ne garantit que les valeurs absolues de r1 et r2 sont premières entre elles. Supposons qu'elles admettent un diviseur commun et notons d leur plus grand commun diviseur. d ne peut diviser p car il diviserait alors a et b qui sont premiers entre eux. En conséquence d divise q1. Soit a' (resp. b' ) le quotient de la valeur absolue de r1 (resp. r2) par d et q'1 le quotient de q1 par d 2. Notons n1 le produit de p par q'1. Alors a' et b' sont deux entiers positifs premiers entre eux tels que :
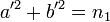
Et l'entier n1 contient un facteur premier p qui n'est pas somme de deux carrés. En réitérant le raisonnement, il existe une suite (ni) strictement décroissante et infinie d'entiers positifs. La logique de la méthode de la descente infinie permet de conclure que chaque facteur premier de n0 est somme de deux carrés.
Lagrange et les formes quadratiques
Si la démonstration d'Euler possède l'avantage de clore une conjecture de plus d'un siècle, elle est difficilement généralisable et ne permet guère de progresser sur l'équation diophantienne x2 + n.y2 = p.
Lagrange utilise une démarche moins entachée de cette faiblesse. Il considère l'expression x2 + y2 comme la forme quadratique associée au produit scalaire canonique. Cette approche élargit considérablement la liste des outils disponibles, ceux de l'algèbre linéaire en font maintenant partie. La situation n'est néanmoins pas celle la plus fréquemment rencontrée. Le produit scalaire n'est pas défini sur un espace vectoriel mais sur le module Z2. Un module est une structure comparable à celle d'espace vectoriel, à la différence près que l'ensemble des scalaires n'est plus un corps. Pour les modules de cette nature, certains résultats restent vrais, comme par exemple l'existence d'une base ce qui offre une expression algébrique simple.
Si M est la matrice de passage de la base canonique dans une autre base sur Z2, son déterminant est nécessairement égal à 1 ou -1. En effet, une matrice de passage est inversible :
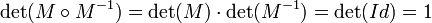
Ici Id désigne la matrice identité. Comme les coefficients de la matrice sont entiers, le déterminant l'est aussi. L'égalité précédente montre que le déterminant de M est inversible et comme les seuls entiers inversibles sont 1 et -1, ce sont les seules valeurs possibles. La matrice du produit scalaire canonique est l'identité. Dans une base quelconque, la matrice est donc de la forme tM.M (ici tM désigne la matrice transposée de M). Une telle matrice est symétrique et de déterminant égal à un car la transposition ne modifie pas le déterminant. Comme le produit scalaire est défini positif, les coefficients diagonaux sont positifs. Réciproquement, Lagrange établit le résultat suivant :
-
- Toute forme bilinéaire sur Z2 dont la matrice est symétrique, de coefficients diagonaux positifs et de déterminant égal à un, admet une base orthonormale.
Ainsi l'image par la forme quadratique associée d'un vecteur de coordonnées (x, y) dans la base orthonormale est égale à x2 + y2. Lagrange choisit la forme bilinéaire φ de matrice M suivante :
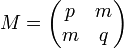
Ici, p désigne le nombre premier congru à un modulo quatre et m et q des entiers. La matrice M possède un déterminant égal à un si et seulement si m2 + 1 = p.q. Cette équation est bien connue et déjà traitée. Elle correspond à l'étude du résidu quadratique -1 sur le modulo p. Elle admet une solution si et seulement si p est congru à un modulo quatre.
Soit u le vecteur de coordonnées (1, 0), un calcul élémentaire montre que φ(u, u) = p. Si a et b sont les coordonnées de u dans la base orthonormale, alors l'expression de φ(u, u) devient a2 + b2, ce qui démontre le théorème.
La démonstration proposée ici est plus riche que celle nécessaire pour démontrer le théorème des deux carrés de Fermat. Si l'objectif est uniquement de prouver le théorème, il suffit de résoudre l'équation (1), ce qui est fait en partie 3) de la démonstration présentée ici.
La démonstration proposée ici montre l'existence d'une base orthonormale pour la forme bilinéaire φ dont la matrice dans la base canonique est égale à M. Dans un premier temps, trouvons un vecteur u ayant pour image par φ l'entier un. Notons (x0, y0) ses coordonnées, entières par définition. Z2 est inclus dans R2 (ici R désigne l'ensemble des nombres réels), la base canonique est aussi une base de R2 et la matrice M permet de prolonger φ sur R2. Soit ψ la forme quadratique associée à φ.
1. Détermination de la coordonnée yR dans R tel que le vecteur de R2 (x0, yR) soit minimal par ψ.
L'application qui à y associe l'image par ψ du vecteur de coordonnées (x0, y) est parabolique et admet un minimum dans R noté yR. On a :
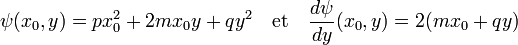
Si m est égal à zéro, le calcul du déterminant montre que p et q sont égaux à un et φ possède bien une représentation matricielle égale à l'identité. Si m est différent de zéro, alors q l'est aussi et :
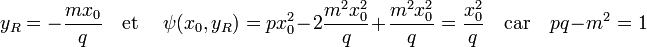
2. Détermination des propriétés de y0.
Le point y0 est l'entier le plus proche de yR. Soit h0 la distance entre ces deux points, c'est-à-dire le réel inférieur à 1/2 en valeur absolue satisfaisant l'égalité : y0 = yR + h0. Ces points vérifient les égalités :
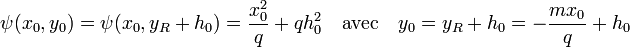
Trouver le point u revient à trouver un vecteur de coordonnées entières (x0, y0) d'image par ψ strictement inférieur à deux, c'est-à-dire si r 0 est égal à q.h0 :

3. Existence de u.
Soit ri le résultat de la division euclidienne de m.i par q, θ l'entier positif tel que θ2 est plus petit ou égal à q et θ2 + 1 est strictement plus grand que q. Considérons l'ensemble des intervalles [i.θ + 1, (i + 1).θ] où i décrit les entiers de zéro à θ et la suite finie (rj) où j décrit les entiers de un à θ.
S'il existe un élément de la suite finie rk se situant dans l'intervalle [0, θ] alors les valeurs k pour x0 et rk pour r0 satisfont les propriétés (1). En effet, rk au carré est plus strictement plus petit que q et k2 + rk2 est strictement plus petit que 2q. Si rk se situe dans le dernier intervalle, alors les valeurs k pour x0 et q - rk pour r0 satisfont encore les propriétés (1). Dans les deux cas, il est possible de construire le vecteur u.
On remarque que la suite (ri) contient θ éléments et qu'il existe θ + 1 intervalles. En conséquence, soit au moins l'un des intervalles extrêmes est couvert par un élément de la suite, soit un intervalle contient deux termes rk et rl (choisissons k plus grand que l). La distance entre les deux termes de la suite est strictement inférieure à θ, en conséquence r k-l est à une distance strictement inférieure à θ de l'un des points 0 ou q et le système (1) admet encore une solution u obtenue avec x0 égal à k-l et pour r0 le minimum de r k-l et q - r k-l.
4. Existence de v tel que (u, v) soit orthonormale pour le produit scalaire φ :
Une fois le vecteur u trouvé, la recherche du deuxième vecteur est plus aisée. Soit Θ la rotation d'un quart de tour dans le sens direct et a l'application linéaire de matrice M dans la base canonique. Soit v l'image de u par aoΘ. Les vecteurs u et v sont bien orthogonaux pour la forme bilinéaire φ. En effet, il suffit de remarquer que a est orthogonal et, si (.,.) désigne le produit scalaire canonique alors :
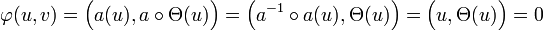
On remarque ensuite que ψ(v) est égal à un :
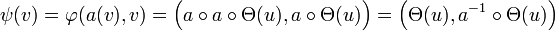
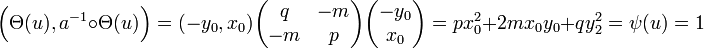
Gauss et ses entiers
L'adjonction d'une géométrie euclidienne à la question des deux carrés est d'un incontestable apport. Elle permet d'introduire les outils de l'algèbre linéaire dans l'arithmétique. Elle ouvre cependant plus de questions qu'elle n'en résout. Bien peu d'outils restent disponibles pour attaquer le cas général. Gauss propose un nouvel enrichissement structurel de l'ensemble des couples de coordonnées entières. Le plan, qui dispose déjà d'une addition, d'un produit externe par un élément de Z et d'une forme quadratique, est en plus équipé d'une multiplication interne. Le point (a, b) de coordonnées entières est identifié au complexe a + i.b. L'ensemble des points dispose alors d'une structure d'anneau dont les éléments sont appelés entiers de Gauss.
La forme quadratique est maintenant interprétée comme une norme. À un point z est associé la norme N(z) définie par le produit de z et de son conjugué. La norme dispose d'un double avantage aux yeux du théorème sujet de l'article, la question posée s'exprime sous une forme simple N(z) = p et la norme est une valuation de l'anneau. Une valuation est ici une application qui à un entier de Gauss associe un entier naturel (le terme entier naturel désigne ici un élément de Z) positif et qui respecte la multiplication, c'est-à-dire si Z[i] désigne l'ensemble des entiers de Gauss :
![\forall z_1,z_2 \in \mathbb Z[i]\quad N(z_1.z_2)=N(z_1).N(z_2)\;](https://static.techno-science.net/illustration/Definitions/autres/4/4202badda5ae4826a098561bab540c73_96148c54af67549a89064199a25b668d.png)
Elle possède l'avantage de conférer à l'anneau une structure euclidienne, c'est-à-dire que l'anneau dispose d'une division euclidienne. Ainsi, si n et m sont deux entiers de Gauss :
![\exists d,r \in \mathbb Z[i]\quad n = d.m + r\quad \text{avec}\quad N(r)<N(d)](https://static.techno-science.net/illustration/Definitions/autres/0/03d38cbf13a03eb9ee554035caf29659_4e37de77afc31b0f3036b024514d1531.png)
Tout anneau euclidien est aussi factoriel, ce qui signifie que le théorème fondamental de l'arithmétique s'applique encore. Il existe ainsi des nombres premiers de Gauss et une décomposition unique en facteur premiers, aux entiers inversibles près.
Ce nouveau cadre structurel autorise la démonstration du théorème en quelques lignes. Si p est un nombre premier congru à 1 modulo 4, l'objectif est de montrer l'existence d'un entier z tel que N(z) = p. Le résultat sur le résidu quadratique -1 montre qu'il existe deux entiers naturels positifs m et k tel que N(m + i) = k.p. On en déduit l'égalité suivante :
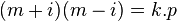
Cette égalité permet de déduire que p n'est pas premier comme entier de Gauss. S'il l'était, il diviserait m + i ou m - i, ainsi que son conjugué. Ainsi il diviserait l'un et l'autre ainsi que leur différence -2.i. Or l'entier de Gauss p ne divise pas -2.i car sa norme est trop grande. Il existe donc deux entiers de Gauss z1 et z2, qui ne sont pas des unités et tel que z1.z2 est égal à p. Comme les diviseurs ne sont pas des unités, leur normes sont différentes de 1 et N(z1).N(z2) = p2. Comme p est premier, les seuls diviseurs de p2 sont 1, p et lui-même. On en déduit que N(z1) est égal à p, ce qui termine la démonstration.