Théorème de prolongement de Tietze - Définition

Introduction

Le mathématicien Pavel Urysohn généralise le résultat de Heinrich Tietze aux espace normaux.

En mathématiques, le théorème de prolongement de Tietze encore appelé de Tietze-Urysohn est un résultat de topologie. Ce théorème indique qu'une fonction continue définie sur un fermé d'un espace topologique X se prolonge continument sur tout l'espace topologique. Le théorème s'applique sur une vaste classe d'espace topologique, il suffit que X soit normal. Il s'applique en particulier sur les espaces métriques ou compacts. Ce résultat généralise le lemme d'Urysohn.

Ce théorème possède de multiples usages en topologie algébrique. Il permet, par exemple de démontrer le théorème de Jordan, indiquant qu'un lacet simple divise l'espace en deux composantes connexes.

Une première version du théorème est l'œuvre du mathématicien Heinrich Tietze pour les espaces métriques, puis généralisée par Pavel Urysohn aux espaces normaux.

Énoncés

L'énoncé le plus classique est le suivant :

• Soit X un espace topologique séparé, les deux propositions suivantes sont équivalentes :

(i) X est un espace normal.

(ii) pour tout fermé A de X et toute application continue f de A dans R, l'ensemble des nombres réels, il existe une application continue g définie sur X qui prolonge f. Autrement dit sur A, f et g coïncident.

On dispose du corollaire suivant :

• Si la fonction f est bornée (resp. strictement bornée) par un réel M, la fonction g peut être choisie bornée (resp. strictement bornée) par M.

Démonstrations

La démonstration s'appuie essentiellement sur le lemme d'Urysohn. Le sens direct est relativement simple :

• Si (ii) est vérifiée, l'espace X est normal :

On suppose (ii). Soit A et B deux fermés disjoints de X et f l'application définie sur l'union de A et de B égale à 1 sur A et à 0 sur B. L'application f est continue car X est séparé. L'hypothèse (ii) montre l'existence d'une fonction continue g prolongeant f sur X. Les images réciproques de [0, 1/2[ et de ]1/2, 1] par g sont deux ouverts disjoints contenant A et B. L'existence de tels ouverts montre que X est un espace normal.

La réciproque s'appuie sur le lemme suivant, vérifiée si X est un espace normal :

• On suppose que f est à valeurs dans un segment [a, b]. Il existe une fonction g_c définie sur X et telle que :

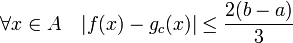
Soit α et β les bornes inférieure et supérieure de l'image de f. Si α est égal à β la fonction f est constante et le lemme est évident, il suffit de choisir comme fonction g_c la fonction constante de même image que f. Sinon, soient A_- (resp. A₊) l'image réciproque de [α, α+ (β - α)/3] (resp. [α+ 2(β - α)/3, β]). Les ensembles A_- et A₊ sont deux fermés non vides de A et donc deux fermés de X. Le lemme d'Urysohn montre l'existence d'une application continue g_c1, définie sur X, qui vaut 0 sur A_- et 1 sur A₊. On définit la fonction g_c par :

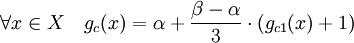
La fonction g_c vérifie la majoration suivante, qui démontre le lemme :

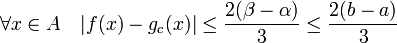
On suppose maintenant que f est une fonction bornée par M et que l'espace X est normal. Le lemme montre qu'il existe une application continue g₁, définie sur X, telle que la différence entre f et g₁ soit inférieure ou égale, en valeur absolue, à 2/3.M sur A. En appliquant n fois le lemme, si n est un entier strictement positif, on en déduit l'existence de n applications continues g_k, définies sur X tel que :

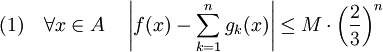
Ce qui permet d'établir la proposition suivante :

• On suppose que X est normal et f bornée par un réel positif M, il existe une série normalement convergente de terme général g_n, où g_n est une application continue définie sur X et à valeurs dans R, telle que la limite de la série, restreinte à A, soit égale à f.

La série est de terme général une application continue et est normalement convergente d'après la majoration (1). Sa limite est une application continue car son terme général l'est. La réciproque est maintenant établie dans le cas où f est une fonction bornée.

• Si X est normal, la proposition (ii) est vérifiée :

Soit f une fonction vérifiant les hypothèses de la proposition (ii) et θ un homeomorphisme de R dans ]0, 1[, la fonction θof est bornée, d'où l'existence d'une application g_int de X dans R continue et telle que la restriction de g_int à A soit égale à θof. Il suffit de considérer l'application g = θ^-1og_int pour conclure.