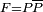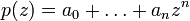Théorème de d'Alembert-Gauss - Définition
La liste des auteurs de cet article est disponible ici.
Démonstrations
Preuve directe
La preuve proposée ici fait appel à un bagage mathématique minimal, elle suit le canevas de celle de Cauchy. On considère une fonction polynôme définie dans C par P(z) = a0 + a1z+...+ anzn tel que n est strictement positif et an non nul. On suppose de plus que a0 est non nul, car sinon le polynôme P admet 0 pour racine évidente et le théorème est trivialement vérifié.
Dans un premier temps, l'existence d'un minimum z0 pour la fonction qui à z associe le module de P(z) est établie. Pour cela, on remarque que si le module de z est suffisamment grand, le module de P(z) l'est aussi et la zone des valeurs minimales pour P(z) est nécessairement bornée. Ensuite, on utilise le fait qu'un fermé borné de C est un compact et qu'une fonction continue d'un compact dans R atteint toujours son minimum.
Enfin, on raisonne par l'absurde, on suppose que l'image de z0 par P est non nulle. On trouve une direction c (un nombre complexe non nul) telle que si t désigne un réel, la fonction de R dans R qui à t associe le module de P(z0 + t.c) est strictement décroissante. On en déduit l'existence d'une valeur t0 telle que le module de P(z0 + t0.c) est strictement plus petit que celui de P(z0). Cette contradiction permet de conclure.
Montrons tout d'abord un lemme, qui correspond à un cas particulier d'équation polynomiale.
-
-
- L'équation xn = a, où a est un nombre complexe et n un entier strictement positif, admet au moins une racine :
-
- Pour démontrer ce résultat, le plus simple est d'écrire a sous sa forme polaire.
![\exists \rho \in \R^+,\; \exists \theta \in [0, 2\pi]\quad a = \rho\cdot \big(\cos (\theta) + i \sin (\theta)\big)](https://static.techno-science.net/illustration/Definitions/autres/4/46222cf53ed386ddd13dce21d4d90880_f0b8d6fbc219ec81a77094e6e2dfad5f.png)
- La formule de De Moivre montre l'existence d'un nombre complexe c tel que cn soit égal à a :
![\text{Si }c = \sqrt[n] \rho\cdot \left(\cos \left(\frac {\theta}n\right) + i \sin \left(\frac {\theta}n\right) \right)\quad\text{alors}\quad c^n = \rho\cdot \big(\cos (\theta) + i \sin (\theta))\big) = a](https://static.techno-science.net/illustration/Definitions/autres/4/46282b7b1752ec9aba0a1f25302e17a4_d5c462a8c7b853e131a6257091face9a.png)
- On en déduit que r est bien une racine de l'équation étudiée.
Étudions maintenant le cas général.
-
-
- Il existe un point z0 tel que le minimum du module de P(z) est atteint en z0 :
-
- La fonction qui à z associe le module de P(z) est à valeurs dans les réels positifs. Tout ensemble non vide et minoré de R admet une borne inférieure. L'ensemble image de la fonction |P(z)| est une partie non vide et minorée de R, elle admet donc un minimum, noté ici m.
- Montrons qu'il existe une valeur M tel que si le module de z est plus grand que M, alors |P(z)| est supérieur à 2.m. L'inégalité triangulaire montre que :
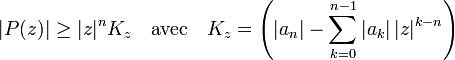
- Si le module de z est suffisamment grand, disons supérieur à une valeur M > 1, le terme Kz est plus grand que |an|/2 et |P(z)| est plus grand que Mn|an|/2. Si M est choisi plus grand que 4.m/|an|, tout point z de module supérieur à M est tel que |P(z)| est plus grand que 2.m. Ceci montre que le minimum de |P(z)| sur les complexes de module inférieur à M est aussi le minimum de |P(z)| sur C.
- Les complexes de modules inférieurs à M forment un compact, la fonction |P(z)| est continue, elle atteint son minimum sur les compacts, il existe donc un complexe z0 tel que |P(z0)| soit égal à m, ce qui démontre la proposition.
Pour une question de simplicité de rédaction, on note Q(z) le polynôme qui à z, associe la valeur P(z0 + z). C'est un polynôme de même degré que P, et dont le module prend au point 0 sa valeur minimum, laquelle vaut m. On utilise les notations :
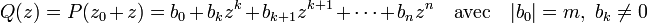
Ici, k désigne le plus petit indice strictement positif tel que le coefficient bk soit non nul. Cet indice existe, car le polynôme est non constant.
Le lemme permet d'établir la proposition suivante, qui aboutit à une conclusion de la démonstration.
-
-
- Le point z0 n'est pas le minimum du module de P(z) si m n'est pas nul :
-
- Soit f(t) la fonction de la variable réelle à valeurs réelles, qui à t associe |Q(t.c)|, ici c désigne un complexe tel que ck soit égal au produit de -b0 et du conjugué de b k (d'après le lemme). La fonction f s'écrit :
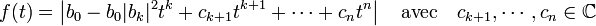
- Ce qui montre que, si t est suffisamment petit en valeur absolue et plus petit que 1 :
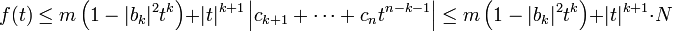
- Dans l'égalité précédente, N désigne un majorant de la somme des valeurs absolues des différentes valeurs de c k. Si les valeurs de t sont, en valeur absolue, choisies plus petites que m.|b k|2/(2.N) On obtient la majoration :
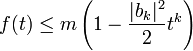
- En conséquence, si t0 est choisi strictement positif et suffisamment petit, f(t0) est strictement plus petit que m, ce qui revient à dire que le module de l'image de z0 + t0.c est strictement plus petit que m, ce qui montre que m n'est pas le minimum et termine la démonstration.
Si m n'est pas nul, ce n'est pas le minimum de la fonction |P(z)|, ce qui est absurde car c'est sa définition. Autrement dit, m est nécessairement nul et P admet au moins une racine z0.
Théorème de Liouville
Une preuve très concise repose sur le théorème de Liouville en analyse complexe. À cet effet, on considère un polynôme P à coefficients complexes, de degré au moins égal à 1. On suppose qu'il n'a aucune racine : dès lors, la fonction rationnelle 1 / P est entière et bornée (car elle tend vers 0 à l'infini, d'après la démonstration précédente) ; du théorème de Liouville, on déduit qu'elle est constante, ce qui contredit l'hypothèse sur le degré, et prouve ainsi par l'absurde l'existence d'au moins une racine de P.
Théorème de Rouché
Une autre preuve concise s'appuie sur le théorème de Rouché en analyse complexe. On considère le polynôme p à valeurs dans
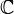
en supposant que le coefficient an est non nul. Il suffit ensuite de comparer ce polynôme à anzn sur un cercle suffisamment grand pour en déduire, en appliquant le théorème de Rouché, que p possède autant de zéros que anzn c'est-à-dire n.
Homotopie
Une homotopie entre deux lacets est une déformation continue permettant de passer du premier lacet au deuxième. L'article détaillé montre que si p est un polynôme de degré n et si ρ est un nombre réel suffisamment grand, le lacet α défini sur le cercle unité par :
![\forall t \in [0,1]\quad \alpha(t) = \frac {p(\rho\exp(2\pi i \cdot t))}{|p(\rho\exp(2\pi i \cdot t))|}](https://static.techno-science.net/illustration/Definitions/autres/e/ebe481faa6ab367fe9d05bea2a0f1871_5a2476dad35b98fa76ca21f94f39b708.png)
fait n fois le tour du cercle. Si le polynôme p n'avait pas de racine, il serait homotope à un point. Cette contradiction est la base de la démonstration proposée dans l'article détaillé.
Théorème des valeurs intermédiaires
Il existe une preuve presque purement algébrique du théorème fondamental de l'algèbre, réécriture moderne de celle conçue par Lagrange. Elle n'utilise l'analyse que pour prouver, par l'élémentaire théorème des valeurs intermédiaires, que tout polynôme réel de degré impair admet une racine (et le fait que tout réel positif est un carré).
Une fois obtenu ce résultat facile, on s'attaque à des polynômes réels de degré peut-être pair (on ne pourra dans ce cas espérer trouver qu'une racine complexe). Une ingénieuse combinatoire qui fait jouer les relations entre coefficients et racines permet de ramener l'étude d'un polynôme de degré disons 6 à une famille de polynômes réels de degré 15 - plus généralement si le polynôme qui nous intéresse est de degré 2nq où q est impair on se ramène à une famille de polynômes réels d'un même degré non divisible par 2n. Ceci laisse entrevoir une récurrence sur la valuation 2-adique du degré du polynôme, qui se révèle effectivement possible.
Traiter les polynômes à coefficients complexes non nécessairement réels n'est plus alors qu'une formalité.
Cette démonstration se généralise au cas des corps réels clos (c'est même ce qui motive leur définition) : si K est un corps réel clos, l'extension L = K(i) est un corps algébriquement clos (i est ici un symbole formel tel que i2+1=0, ce qui revient à définir L comme le quotient de K[X] par le polynôme X2 + 1) ; ce théorème est "attribué" par Nicolas Bourbaki à Euler et Lagrange
-
-
- Tout polynôme réel de degré impair possède une racine réelle :
-
- En effet, si le polynôme réel est de degré impair, ses limites en plus et moins l'infini sont de signes opposés, le théorème des valeurs intermédiaires montre l'existence d'une racine.
On en a fini avec l'analyse et on passe au cœur de la preuve, en prouvant que :
-
-
- Tout polynôme réel possède une racine complexe :
-
- Pour F polynôme réel, on note d son degré, puis on pose d = 2nq, où q est impair. La preuve est une récurrence sur n, l'initialisation n=0 ayant été traitée par la technique analytique.
- Supposons le résultat connu pour tous les polynômes réels de degré non divisible par 2n et soit F réel de degré d = 2nq (q impair). On peut, quelques instants, considérer F comme à coefficients complexes et introduire un corps de décomposition K pour F (comme on a pensé provisoirement F dans C[X], C⊆K) ; on note alors xi (1 ≤ i ≤ d) ses racines dans K (éventuellement répétées autant de fois qu'elles sont multiples).
- Pour chaque réel c on introduit le polynôme :
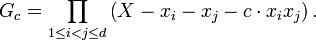
- Ce polynôme est de degré d(d-1)/2 = 2n-1q(d-1) qui n'est pas divisible par 2n. Les coefficients de Gc sont par ailleurs réels : en effet ce sont des polynômes symétriques à coefficients réels en les racines de F, ils peuvent donc être écrits comme des polynômes réels en les polynômes symétriques élémentaires en les racines de F, donc comme des polynômes réels en les coefficients de F, coefficients qu'on a supposés réels. On peut dès lors appliquer l'hypothèse de récurrence à Gc et conclure qu'une au moins de ses racines est complexe. On peut donc isoler deux indices i(c) et j(c) tels que :
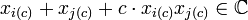
- L'ensemble R est infini alors que l'ensemble des couples d'indices est fini, et il existe deux réels c et d tels que i(c) = i(d) et j(c) = j(d) ; on note i = i(c) = i(d) et j = j(c) = j(d). Comme (xi + xj) + c(xixj) et (xi + xj) + d(xixj) sont complexes avec c ≠ d, on en déduit que xi + xj et xixj sont aussi complexes, puis que xi et xj sont à leur tour racines d'un polynôme du second degré à coefficients complexes, donc complexes.
On a bien trouvé une racine complexe pour F (et même deux) .
-
-
- Fin de la preuve
-
- Pour P polynôme à coefficients complexes, on considère le polynôme