Théorème de Thalès - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le théorème de Thalès ou théorème d'intersection est un théorème de géométrie qui affirme que, dans un plan, une droite parallèle à l'un des côtés d'un triangle sectionne ce dernier en un triangle semblable (voir énoncé précis ci-dessous). Dans certains pays d'Europe, dont la France, ce résultat est appelé théorème de Thalès ; en anglais il est connu sous le nom de théorème d'intersection, moins commun en français ; en allemand il est appelé Strahlensatz, c'est-à-dire théorème des rayons.
Ce résultat est attribué au mathématicien et philosophe grec Thalès de Milet. Cette attribution s'explique par une légende selon laquelle Thalès aurait calculé la hauteur d'une pyramide en mesurant la longueur de son ombre au sol et la longueur de l'ombre d'un bâton de hauteur donnée. Cependant, certains documents historiques montrent que les similitudes des triangles avaient déjà été remarquées par les Babyloniens. Mais la première démonstration écrite connue de ce théorème est donnée dans les Éléments d'Euclide (proposition 2 du livre VI). Elle repose sur la proportionnalité d'aires de triangles de hauteur égale (voir ci-dessous le détail de la preuve).
Le théorème de Thalès se généralise en dimension supérieure. Le résultat est équivalent à des résultats de géométrie projective tels que la conservation du birapport par les projections. À un niveau plus élémentaire, le théorème de Thalès sert à calculer des longueurs en trigonométrie, à condition de disposer de deux droites parallèles. Cette propriété est utilisée dans des instruments de calcul de longueurs.
En anglais et en allemand, le théorème de Thalès désigne un autre théorème de géométrie qui affirme qu'un triangle inscrit dans un cercle, et dont un côté est un diamètre, est un triangle rectangle.
Énoncés et enseignement
En pratique, le théorème de Thalès permet de calculer des rapports de longueur et de mettre en évidence des relations de proportionnalité en présence de parallélisme.
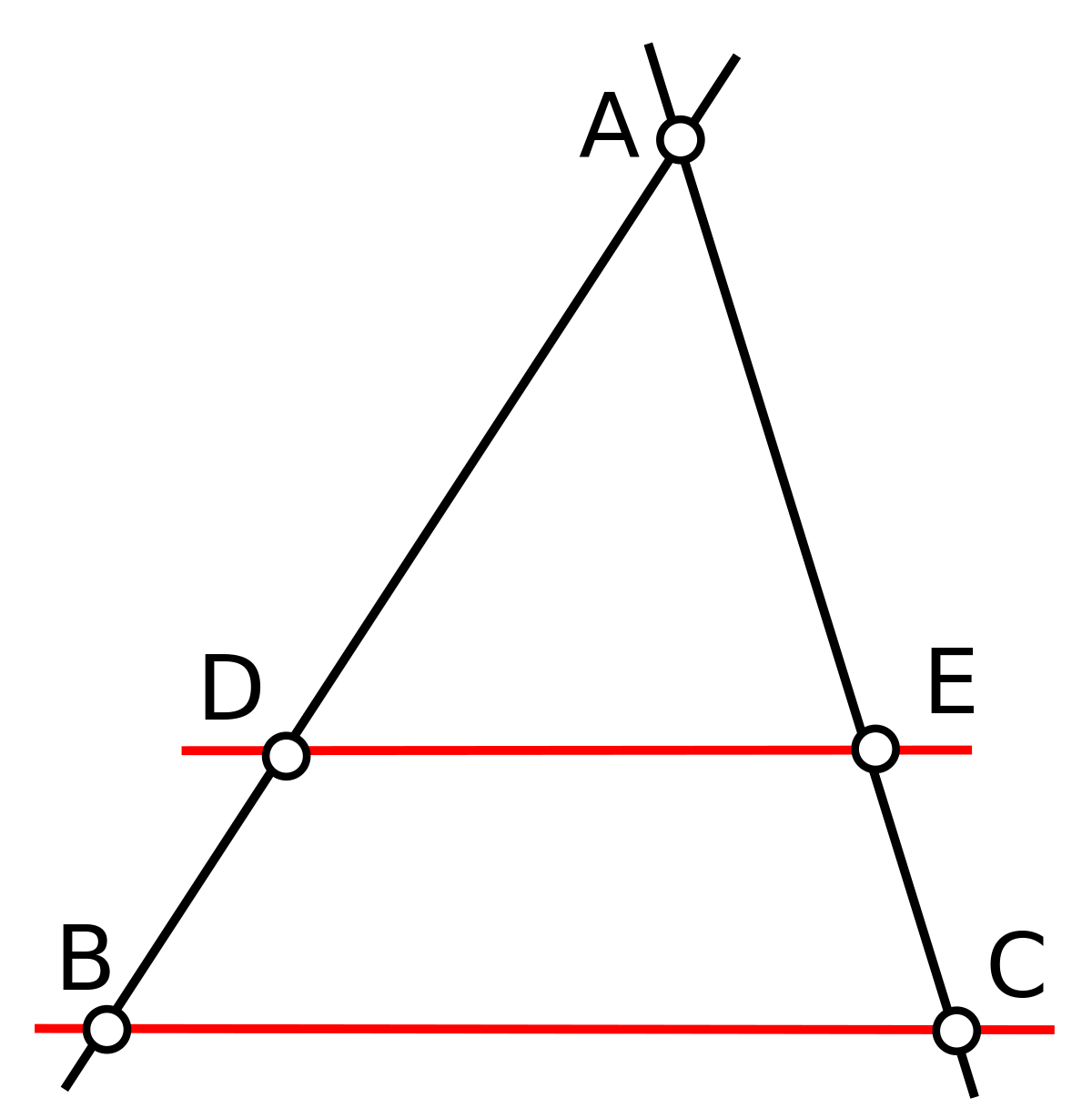
- Théorème de Thalès :Soit un triangle ABC, et deux points D et E des droites (AB) et (AC) de sorte que la droite (DE) soit parallèle à la droite (BC) (comme indiqué sur la figure ci-dessous). Alors on a :
-
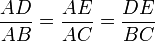
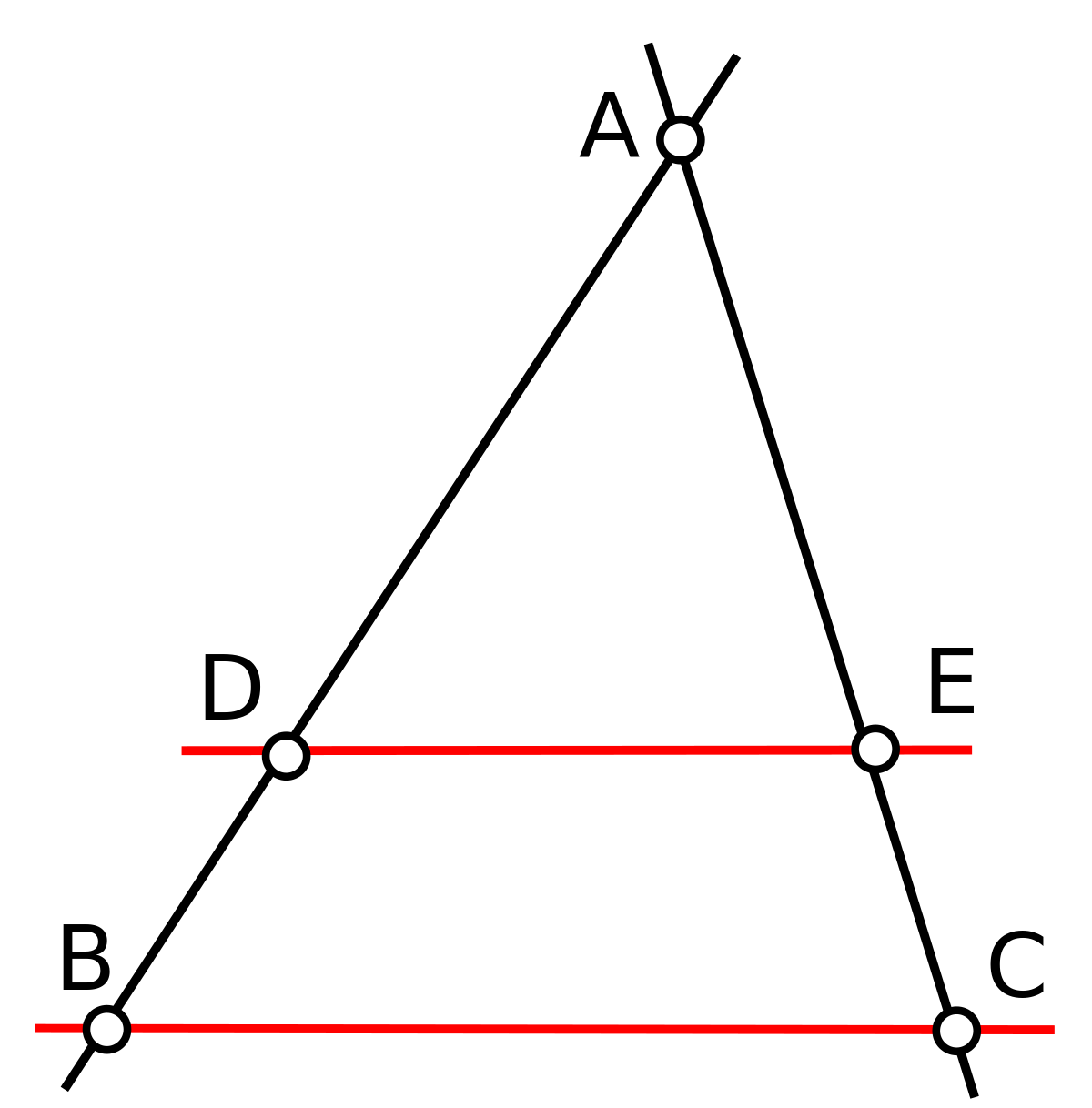
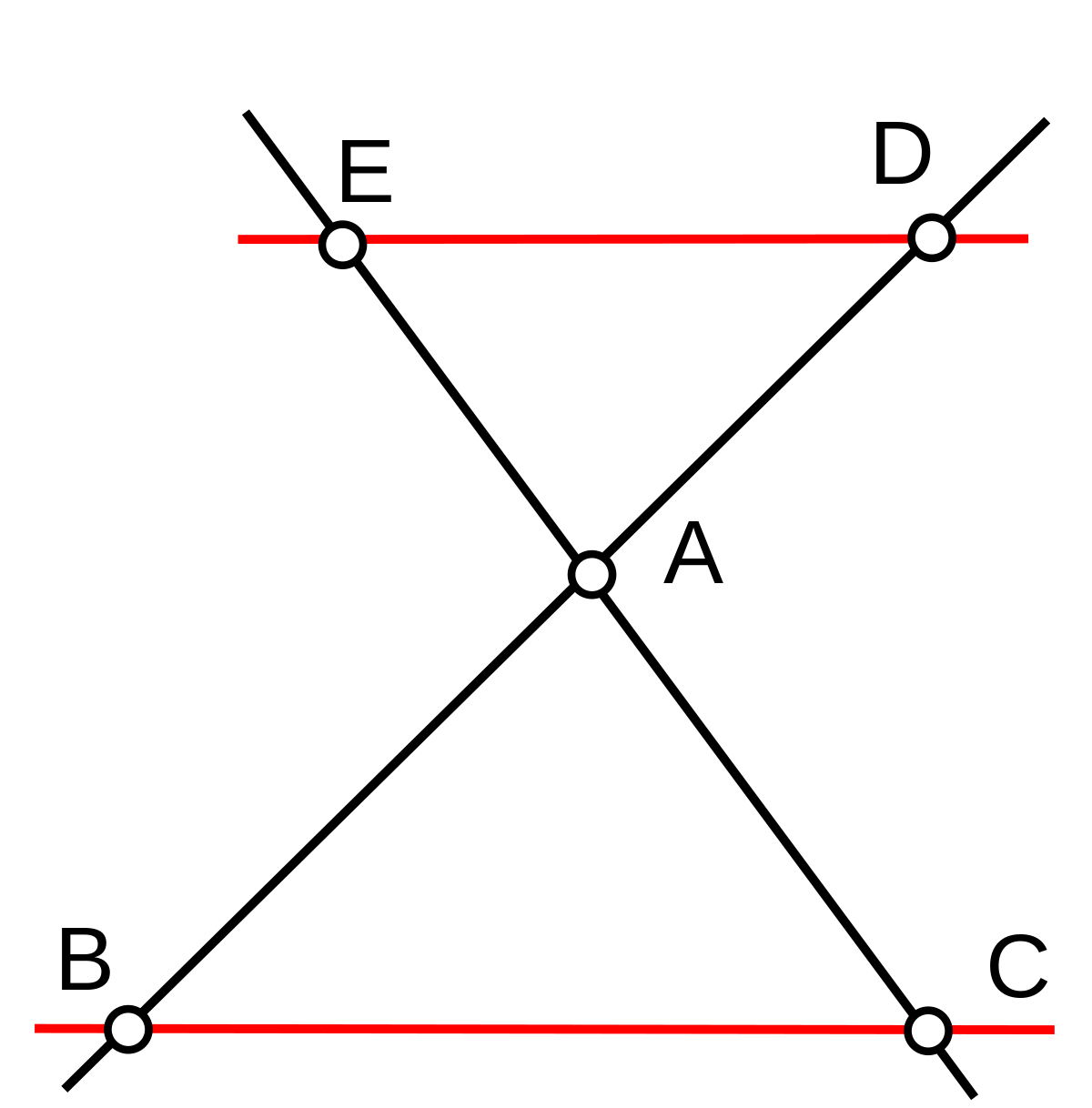
Deux configurations possibles du théorème de Thalès.
Le théorème de Thalès démontre que les triangles ABC et ADE sont homothétiques : il existe une homothétie de centre A envoyant B sur D et C sur E. L'un des rapports donnés ci-dessus est au signe près le rapport de l'homothétie. Plus précisément, le rapport de l'homothétie est + AD / AB dans la première configuration et − AD / AB dans la seconde. Le théorème de Thalès est parfois énoncé plus simplement en affirmant qu'une droite parallèle à un des côtés du triangle coupe ce triangle en un triangle semblable.
Il peut être mis en œuvre dans différentes constructions géométriques faisant intervenir compas et règle. Par exemple, il peut justifier une construction permettant de diviser un segment en un nombre donné de parts égales.
Pour être plus rigoureux, l'énoncé ci-dessus donné nécessite l'utilisation d'une distance euclidienne pour donner un sens aux longueurs mentionnées (AB, BC, ...). Un énoncé plus général et précis est donné dans le cadre de la géométrie affine. Dans ce cadre, la notion de longueur est remplacée par celle de mesure algébrique, et seul le rapport a un sens (voir plus loin).
Théorème réciproque
Le théorème de Thalès (en dimension 2), dans son sens direct, permet de déduire certaines proportions dès que l'on connaît un certain parallélisme. Sa réciproque permet de déduire un parallélisme dès que l'on connaît l'égalité de certains rapports.
- Réciproque du théorème de Thalès : Dans un triangle ABC, supposons donnés des points D et E appartenant respectivement au segment [AB] et [AC]. Si les rapports AD/AB et AE/AC sont égaux, alors les droites (DE) et (BC) sont parallèles.
Il est à remarquer que la démonstration de cette réciproque se déduit du théorème. En effet, considérons un point E' du segment [AC] tel que (DE') soit parallèle à (BC). Alors les points A, E', C sont alignés dans cet ordre et AE'/AC = AD/AB = AE/AC donc il vient que AE' = AE. Or il n'existe qu'un seul point situé entre A et C vérifiant cette propriété donc E' = E . Par conséquent, (DE)=(DE') est parallèle à (BC).
Il est à noter que ce qui est appelé "le théorème réciproque de Thalès" n'est pas la réciproque, au sens logique du terme, du théorème initial.
Théorème de la droite des milieux
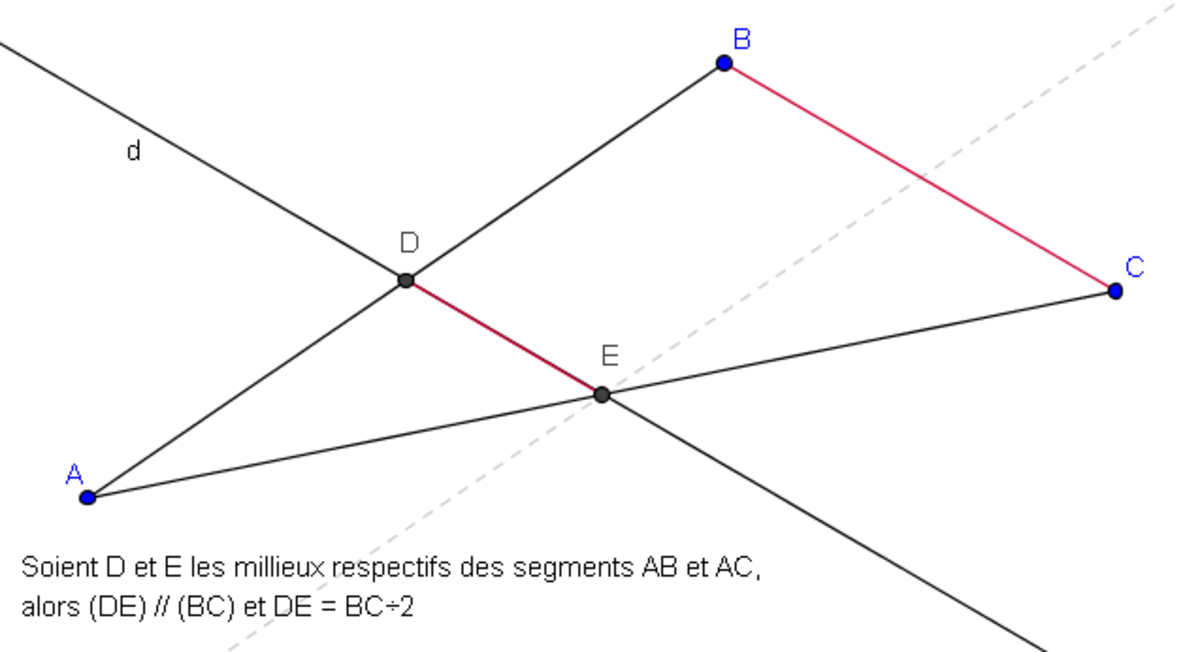
Le théorème des milieux est une spécialisation du théorème de Thalès, pour laquelle les points D et E correspondent aux milieux des segments [AB] et [AC]. Si une droite passe par les milieux de deux côtés d'un triangle, elle est parallèle à la droite qui supporte le troisième côté ; et la longueur joignant les milieux des deux côtés est égale à la moitié de la longueur du troisième côté:
- Théorème de la droite des milieux : Soit un triangle ABC, et nommons D et E les milieux respectifs de [AB] et [AC]. Alors les droites (DE) et (BC) sont parallèles et on a : 2.DE = BC.
La réciproque du théorème de Thalès justifie que les deux droites sont parallèles ; de plus, le théorème de Thalès s'applique et il vient :
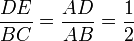
Enseignement et appellations
Ce théorème est connu sous le nom de théorème de Thalès dans l'enseignement des mathématiques en France, en Suisse, etc..
Aucun texte ancien ne semble attribuer la découverte d'un résultat semblable à Thalès. La première référence où une telle attribution est faite se trouve dans les Éléments de géométrie de Rouché et Comberousse en 1883. Une des causes de cette attribution serait l'incitation faite aux agrégatifs à la fin du XIXe siècle d'attribuer aux résultats des noms de mathématiciens pour qu'ils s'intéressent à l'histoire des mathématiques.
C'est aussi sous le nom de théorème de Thalès que le résultat est connu dans les pays de la Méditerranée et dans les pays de l'Europe de l’Est ou du Nord. Cependant, dans les pays de langue anglaise et en Allemagne, ce résultat est connu sous le nom de théorème d'intersection.
L'appellation théorème de Thalès désigne dans ces pays la propriété selon laquelle tout angle inscrit dans un demi-cercle est droit (lire Théorème de Thalès (cercle)).
En Suisse, le théorème est principalement abordé au moyen de la « petite propriété de Thalès » telle qu'elle est enseignée en France. Le « théorème de Thalès suisse » exprime par contre le carré de la hauteur dans un triangle rectangle.