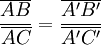Théorème de Thalès - Définition

Généralisations du théorème de Thalès

Cas de trois droites parallèles

Disposition des points et des droites.

Toujours en dimension 2, le théorème de Thalès désigne souvent l'énoncé suivant, qui utilise les mesures algébriques :

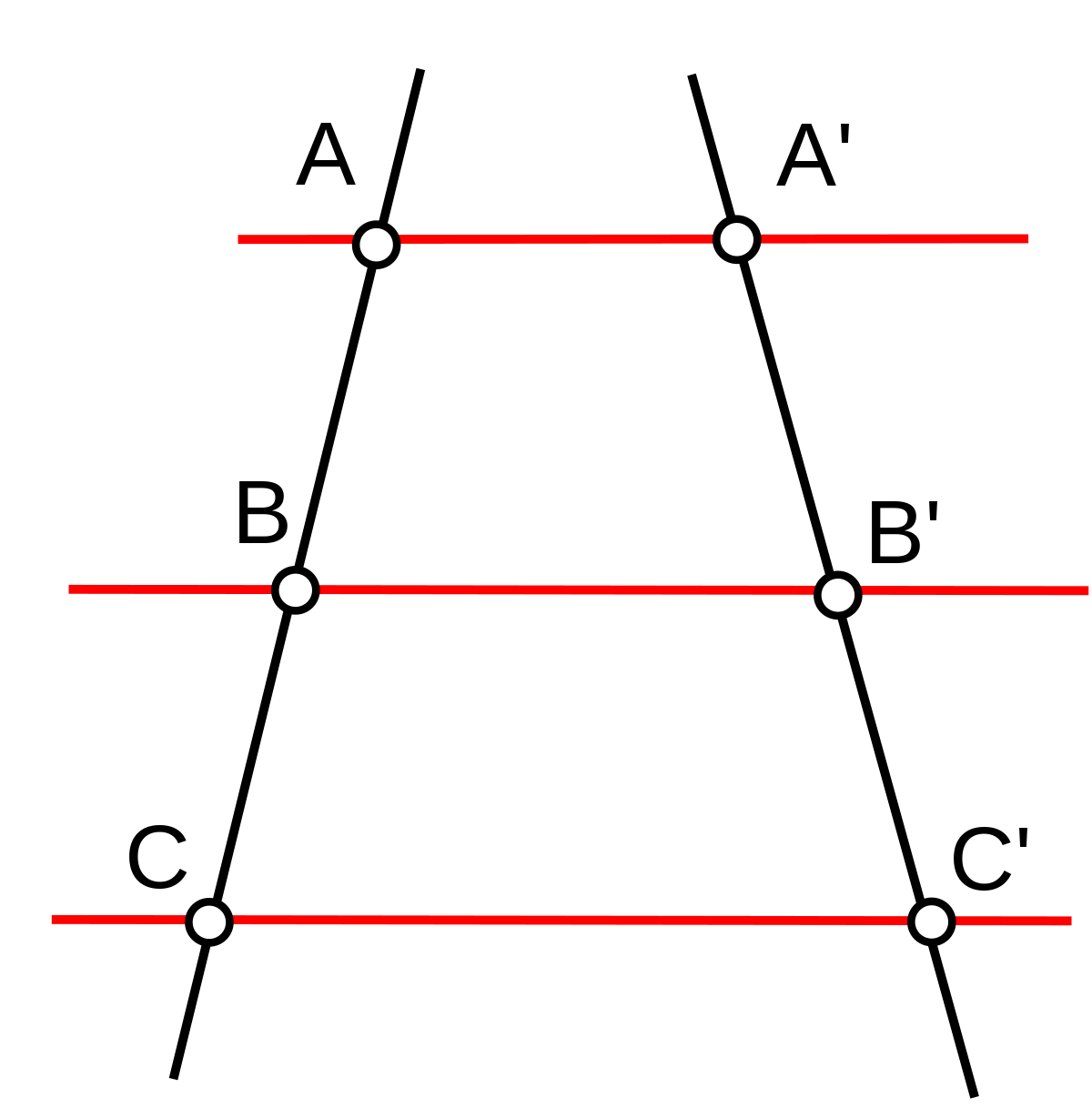
Théorème de Thalès : Soient deux droites d et d' (du plan réel euclidien) et trois droites parallèles (AA'), (BB') et (CC') intersectant d et d' respectivement en A et A', en B et B', et en C et C', comme indiqué sur la figure ci-contre. Alors :

.

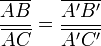
Cette conclusion équivaut à l'une des deux égalités suivantes :

ou  ;

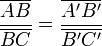
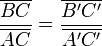
ou encore à :

.

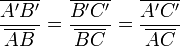
Si on néglige les mesures algébriques, le premier énoncé donné du théorème de Thalès est la spécialisation du second au cas où deux points sont confondus (par exemple A et A'). En considérant la parallèle à d' passant par A le second énoncé se déduit du premier.

Il est possible de donner une démonstration de ce théorème à partir de l'axiomatique du plan arguésien dégagée au XX^e siècle.

En dimension supérieure

Souvent énoncé comme un théorème de géométrie plane, le théorème de Thalès se généralise sans difficulté en dimension supérieure, notamment en dimension 3. L'utilisation de droites parallèles est remplacée par des hyperplans parallèles ; les droites (d) et (d') n'ont pas à être supposées coplanaires :

Théorème de Thalès : Soient (d) et (d') deux droites d'un même espace affine ; et H_a, H_b et H_c trois hyperplans parallèles. On suppose en outre que la droite (d) intersecte les hyperplans respectivement en A, B, C, et de même que la droite (d') respectivement en A', B' et C'. Alors, on a :

Quand les deux droites (d) et (d') ne sont pas coplanaires, ce théorème connait une réciproque sous la forme suivante : quand les points A, B, C distincts sur (d) et les points A', B', C' distincts sur (d') vérifient l'égalité des rapports de mesure algébrique ci-dessus, il existe alors trois plans parallèles contenant le premier A et A', le second B et B' et le troisième C et C'.

Preuve utilisant une projection affine

Dans son livre, Marcel Berger propose une preuve algébrique de la version du théorème de Thalès en dimension supérieure. Sa preuve ne s'appuie pas sur une approche axiomatique de la géométrie, mais sur la définition actuelle d'espace affine et vectoriel.

La preuve de Marcel Berger consiste à construire une bijection affine f entre les deux droites d et d' envoyant A sur A', B sur B', et C sur C'. Il est possible de déduire de la définition d'une application affine qu'une bijection affine entre droites affines préserve le rapport. Donc :

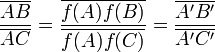
Pour construire effectivement f, Marcel Berger propose de munir l'ensemble des hyperplans parallèles à H_a d'une structure de droite affine (structure quotient), de sorte que l'application qui à un point de d (ou bien de d') associe l'hyperplan passant par ce point et parallèle à H_a soit une application affine. Sans introduire la notion d'espace quotient, on peut aussi définir l'application f comme la restriction à d de la projection sur la droite d' parallèlement à H_a. Par définition, f envoie effectivement A sur A', B sur B', et C sur C'. L'inverse de f se définit comme la restriction à la droite d' de la projection sur d parallèlement à H_a.

Conservation des birapports par les projections

Le birapport est un invariant projectif associé à quatre points. Le théorème de conservation des birapports par projection est lié de près au théorème de Thalès, l'un pouvant sans grand mal se déduire de l'autre.

De même que les trois droites parallèles du théorème de Thalès peuvent être remplacées par des hyperplans parallèles dans un espace affine de dimension supérieure à 2, les quatre droites concourantes de ce théorème de conservation des birapports peuvent être remplacées par des hyperplans appartenant à un même faisceau en dimension supérieure.

L'intérêt de ce point de vue est de souligner l'analogie du « rapport » intervenant dans le théorème de Thalès avec le birapport utilisé en géométrie projective : le premier est laissé invariant par une transformation affine d'une droite affine vers une autre exactement comme le second est laissé invariant par une transformation projective d'une droite projective vers une autre.