Théorème de Stokes - Définition
La liste des auteurs de cet article est disponible ici.
Sens physique de la formule de Stokes
Notons
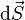
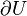
On définit le flux de X par :
La formule d'Ostrogradsky se réécrit alors :
Soit
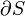
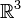
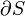
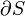
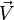
où
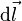
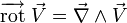
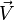
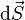
Son application directe est le théorème d'Ampère (on l'applique au champ magnétique).
Formule d'Ostrogradsky
Soit U un domaine compact à bord lisse de
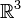
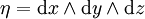
La formule de Stokes donne alors :
Application à l'homologie
La formule de Stokes est utilisée pour démontrer le théorème de dualité de De Rham.
La formule de Stokes permet aussi de démontrer le lemme de Poincaré. Ce dernier s'avère d'une grande utilité pour comprendre les isotopies en homologie. Il est aussi utilisé notablement dans la preuve du théorème de Darboux en géométrie symplectique.
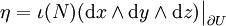
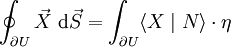
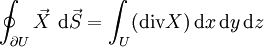
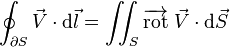
![\mathrm d\left[\iota_X\omega\right]=\mathrm{div}(X)\cdot\omega](https://static.techno-science.net/illustration/Definitions/autres/1/180a7237afb65cd7998a2000a2e9546a_8221c9245fcc4d4b115c691f0c5d3a90.png)
![\int_{\partial U}\! \left[f\cdot \mathrm dy\wedge \mathrm dz+g\cdot \mathrm dz\wedge \mathrm dx+h\cdot \mathrm dx\wedge \mathrm dy\right]=\iiint_U\! \left[\frac{\partial f}{\partial x}+\frac{\partial g}{\partial y}+\frac{\partial h}{\partial z}\right]\, \mathrm dx\,\mathrm dy\,\mathrm dz](https://static.techno-science.net/illustration/Definitions/autres/a/ad1716607f29931a257b4c8d3d36f9c1_2047cd9f3cf4f4deca11181199d7f0e8.png)

















































