Théorème de Pythagore - Définition

Introduction

Une version géométrique du théorème.

Le théorème de Pythagore est un théorème de géométrie euclidienne qui énonce que dans un triangle rectangle (qui possède un angle droit) le carré de la longueur de l’hypoténuse (côté opposé à l’angle droit) est égal à la somme des carrés des longueurs des deux autres côtés. Ce théorème est nommé d’après Pythagore de Samos, mathématicien, philosophe et astronome de la Grèce antique.

Énoncé du théorème

La forme la plus connue du théorème de Pythagore est la suivante :

Note: Le terme « longueur », généralement oublié, est très important. En effet, la longueur est un nombre réel sur lequel l’opération d’élévation au carré est parfaitement définie ; l’hypoténuse est un segment de droite, objet géométrique pour lequel l’élévation au carré n’a pas de sens.

Cependant, il est parfois retiré afin de ne pas compliquer l'apprentissage du théorème (La notion de longueur étant sous-entendue)

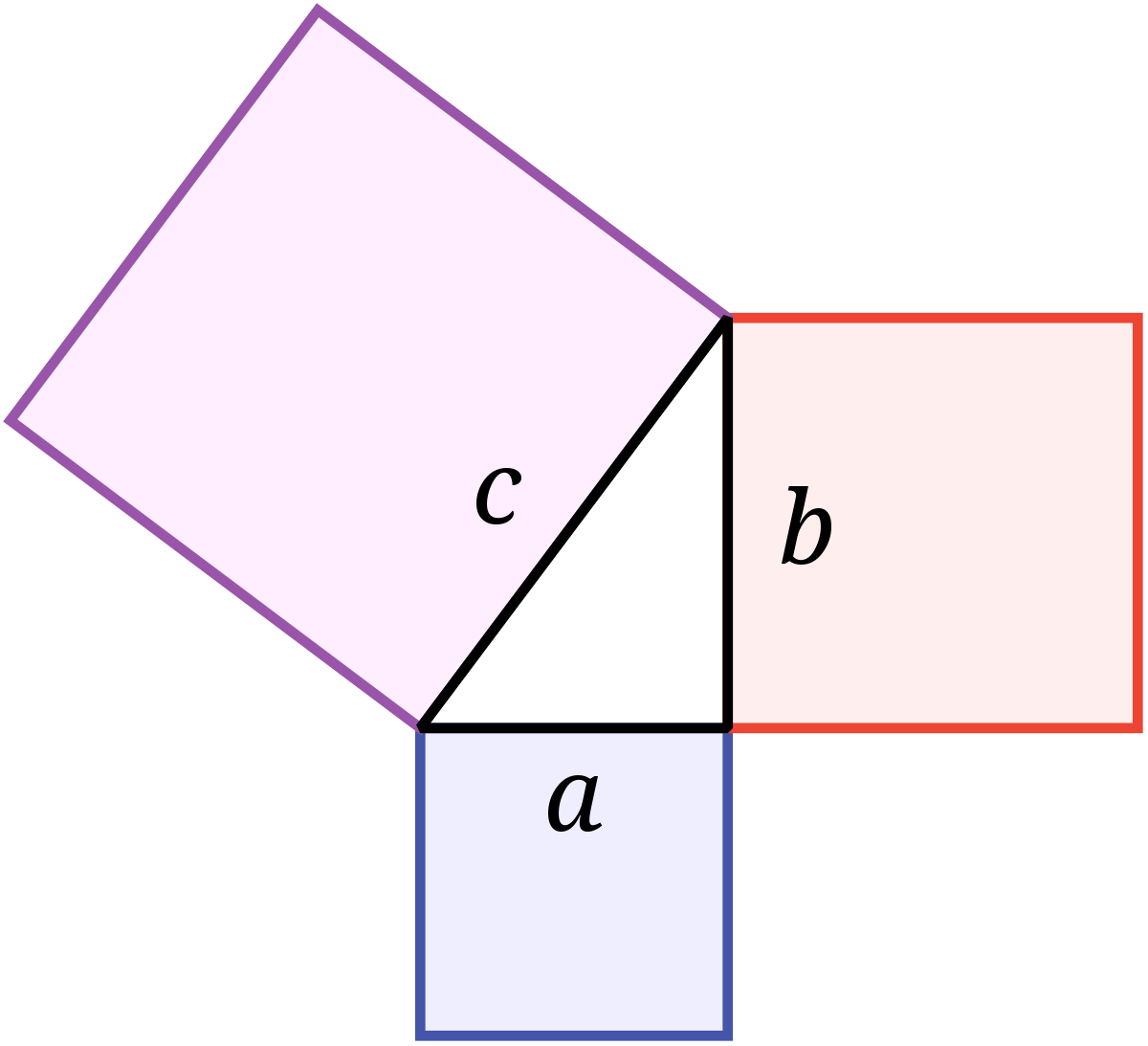
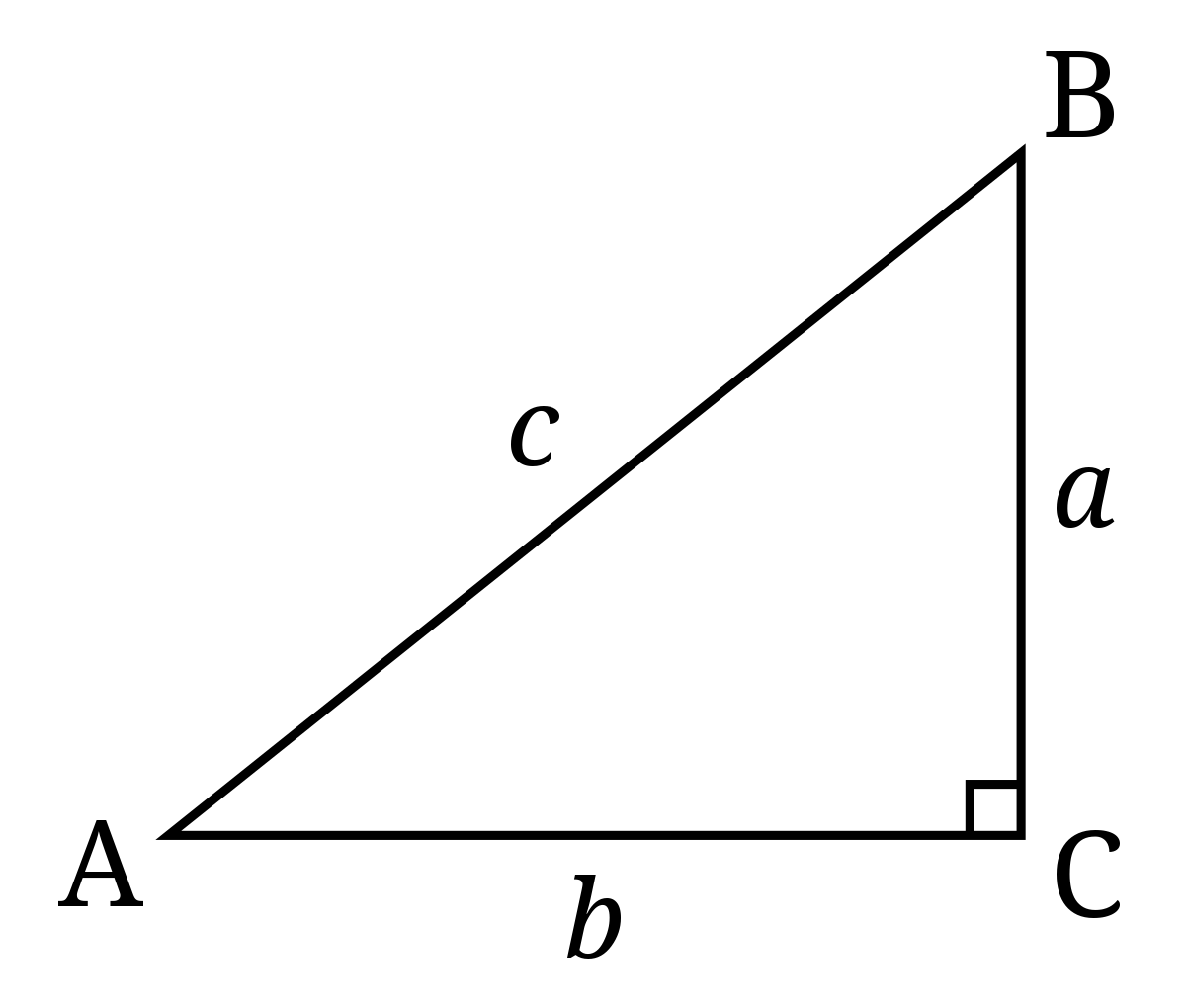
Dans un triangle ABC rectangle en C, AB étant l’hypoténuse, où AB = c, AC = b et BC = a (cf. figure ci-dessus), on aura donc : BC² + AC² = AB² ou encore a² + b² = c².

Le théorème de Pythagore permet ainsi de calculer la longueur d’un des côtés d’un triangle rectangle si on connaît les deux autres.

Exemple

Avec les notations ci-dessus, soit le triangle rectangle de côtés a = 3 et b = 4; alors la longueur du troisième côté, c, est donnée par : a² + b² = 3² + 4² = 25 = c². Les longueurs étant des réels positifs, on obtient c = 5. Un triplet de nombres entiers tel que (3, 4, 5), représentant la longueur des côtés d’un triangle rectangle s’appelle un triplet pythagoricien.

Histoire

Que la propriété de Pythagore soit connue depuis l’Antiquité est un fait dont on peut trouver trace dans l’histoire. Il suffit pour cela d’observer la corde à treize nœuds dont se servaient les arpenteurs égyptiens. Cette corde permettait de mesurer des distances mais aussi de construire, sans équerre, un angle droit puisque les 13 nœuds (et les douze intervalles) permettaient de construire un triangle dont les dimensions étaient (3 - 4 - 5), triangle qui s’avère être rectangle. Cette corde restera un outil de géomètre pendant encore tout le Moyen Âge. La plus ancienne représentation de triplets pythagoriciens (triangle rectangle dont les côtés sont entiers) se trouve sur des mégalithes (au XXV^e siècle av. J.-C., Grande-Bretagne). On retrouve aussi la trace de triplets pythagoriciens sur des tablettes babyloniennes (tablette de Plimpton 322 au XVIII^e siècle av. J.-C. qui prouvent que, plus de 1 000 ans avant Pythagore, les géomètres connaissaient l’existence de triplets pythagoriciens. Mais entre le constat : « on observe que certains triangles rectangles vérifient cette propriété », sa généralisation : « il semble que tous les triangles rectangles vérifient cette propriété » et sa démonstration : « il est vrai que tous les triangles rectangles dans un plan euclidien vérifient cette propriété », il faut souvent attendre plusieurs siècles.

Pythagore

Les preuves historiques de la vie de Pythagore sont déjà si rares qu’il n’est pas étonnant qu’on ne puisse pas lui attribuer avec certitude la paternité de la démonstration. La première trace écrite figure dans les Éléments d’Euclide (proposition XLVII) sous la forme suivante :

« Aux triangles rectangles, le carré du côté qui soutient l'angle droit, est égal aux carrés des deux autres côtés. »

Sa réciproque est la proposition XLVIII :

« Si le carré de l’un des côtés d’un triangle est égal aux carrés des deux autres côtés, l’angle soutenu par ces côtés est droit. »

Cependant, les commentaires de Proclos des Éléments d’Euclide (Autour de 400) semblent indiquer qu’Euclide n’aurait fait que retranscrire une démonstration plus ancienne que Proclos attribue à Pythagore. C’est donc entre le VI^e siècle av. J.-C. et le III^e siècle av. J.-C. que l’on peut dater la démonstration de cette propriété. On raconte que c’est à cette occasion qu’aurait été découverte l’existence de nombres irrationnels. En effet, il est facile de construire un triangle rectangle isocèle de côté 1. Alors le carré de l’hypoténuse vaudrait 2. Or une démonstration simple accessible du temps de Pythagore prouve qu’aucun rationnel n’a un carré égal à 2. On raconte que cette découverte fut tenue secrète par l’école pythagoricienne sous peine de mort.

Parallèlement à ces découvertes, il semble qu’en Chine aussi la propriété soit connue. On retrouve trace de l’existence de ce théorème dans un des plus anciens ouvrages mathématiques chinois le Zhoubi suanjing. Cet ouvrage, écrit probablement durant la dynastie Han (-206 à 220), regroupe des techniques de calcul datant de la dynastie Zhou (X^e siècle av. J.-C. à -256). Une démonstration du théorème, qui porte en Chine le nom de théorème de Gougu (base et altitude), figure dans le Jiuzhang suanshu (Les neuf chapitres sur l'art mathématique, -100 à 50), démonstration qui ne ressemble en rien à celle d’Euclide et qui prouve l’originalité de la démarche chinoise.

En Inde, vers -300, on trouve la trace d’une démonstration numérique de la propriété (preuve effectuée sur des nombres particuliers mais qui peut se généraliser aisément). D’une propriété géométrique, le théorème de Pythagore prend aussi un développement arithmétique avec la recherche de tous les triplets d’entiers associés aux trois côtés d’un triangle rectangle : ce sont les triplets pythagoriciens. Cette recherche ouvrira la porte à une autre : la recherche de triplets vérifiant l’égalité aⁿ + bⁿ = cⁿ, recherche qui conduit à la conjecture de Fermat résolue en 1994 par Andrew Wiles. Il existe en réalité de nombreuses démonstrations de ce théorème, de celle d’Euclide à celle des Chinois, en passant par celle de l’Inde, celle utilisant des similitudes, celle de Léonard de Vinci et même celle du président américain James Garfield. On ne peut pas passer sous silence Al Kashi qui donne pour un triangle quelconque une relation dont la formule de Pythagore devient alors le cas particulier du triangle rectangle : le Théorème d'Al-Kashi.