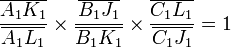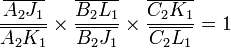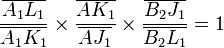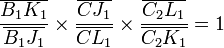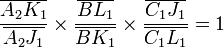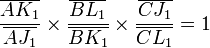Théorème de Pappus - Définition

Notions connexes

• Le Théorème d'Hessenberg qui fait le lien entre le théorème de Pappus et le théorème de Desargues.
• Le théorème de Pappus-affine dans le plan affine.
• L'Hexagramme de Pascal dont la configuration de Pappus est une version dégénérée (la conique est une bidroite).
• Enfin il est indispensable de rappeler que la configuration de Pappus est un bel exemple de Dualité (géométrie projective).

Démonstration à l'aide du théorème de Ménélaüs

Démonstration du théorème de Pappus à l'aide de Ménélaüs

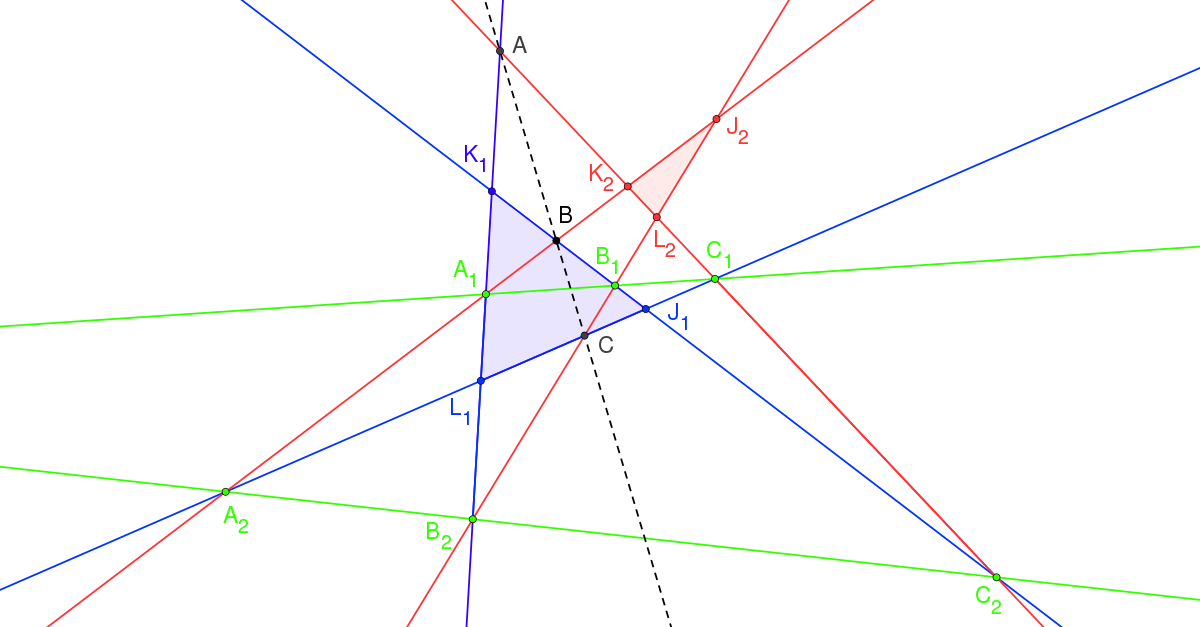
Dans le cas où aucun point n'est impropre et à condition qu'il existe un triangle de référence, dont les côtés soient interceptés par cinq droites du problème, on peut caractériser l'alignement de cinq triplets de points grâce au théorème de Ménélaüs et en déduire simplement que les trois points A, B et C sont alignés. Deux triangles de référence peuvent être choisis à cette fin :

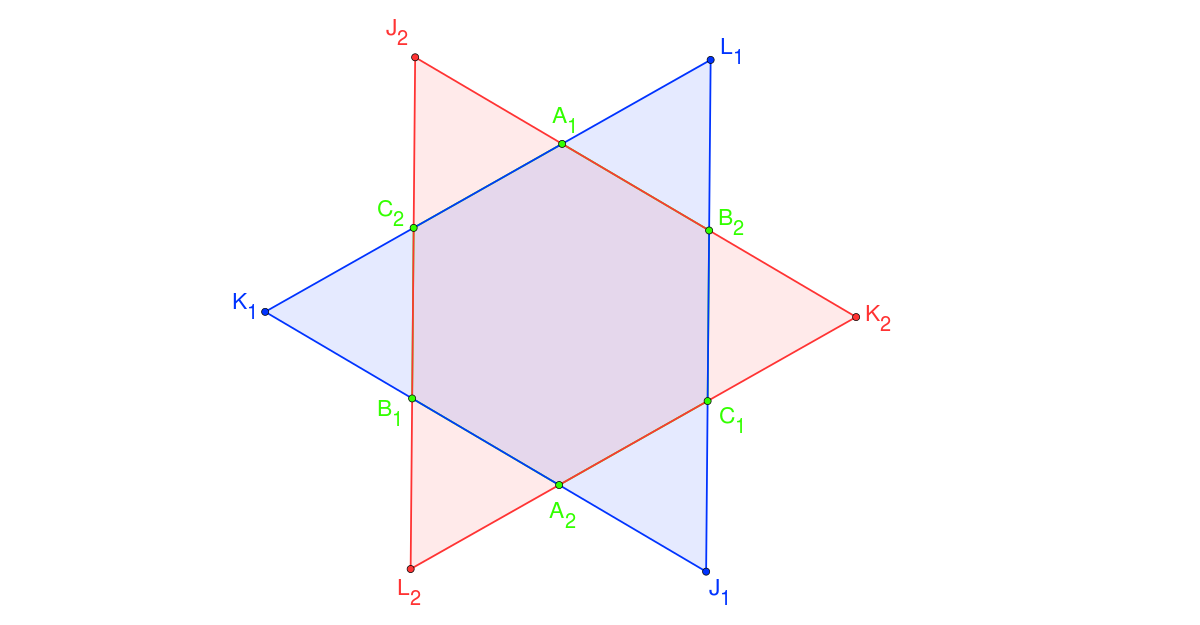
• le triangle J₁K₁L₁ (en bleu sur la figure) dont les sommets sont les intersections des droites (A₂B₁), (B₂C₁) et (A₁C₂),
• le triangle J₂K₂L₂ (en rouge sur la figure) dont les sommets sont les intersections des droites (A₁B₂), (B₁C₂) et (A₂C₁).

Dans le triangle J₁K₁L₁ (s'il existe) :

• la droite (A₁C₁) intercepte les trois côtés en A₁, B₁, C₁
• la droite (A₂C₂) intercepte les trois côtés en A₂, B₂, C₂
• la droite (A₁B₂) intercepte les trois côtés en A₁, A, B₂
• la droite (B₁C₂) intercepte les trois côtés en B₁, C, C₂
• la droite (A₂C₁) intercepte les trois côtés en A₂, B, C₁

D'après Ménélaüs, ces alignements se traduisent par les égalités suivantes :

En multipliant membre à membre ces cinq égalités, il reste après simplification :

ce qui prouve d'après la réciproque de Ménélaüs l'alignement des trois points A, B et C.

Une démonstration analogue peut être faite dans le triangle J₂K₂L₂. Dans ce cas, les trois droites (A₁B₂), (B₁C₂) et (A₂C₁) (en rouge sur la figure) échangent leur rôle avec les trois droites (A₂B₁), (B₂C₁) et (A₁C₂) (en bleu sur la figure). Cette fois-ci, les trois premières droites délimitent le triangle de référence tandis que les trois dernières interceptent les côtés du triangle de référence. Les droites (A₁C₁) et (A₂C₂) (en vert sur la figure) sont conservées pour intercepter le triangle.

Il existe un moyen pratique de trouver les deux triangles de référence. On peut représenter la ligne brisée A₁, B₂, C₁, A₂, B₁ et C₂ sous la forme d'un circuit hexagonal. Les côtés opposés de cet hexagone ont pour intersection les 3 points A, B, C et les deux triangles de référence sont les deux triangles bâtis sur l'hexagone.

Circuit hexagonal et triangles de référence

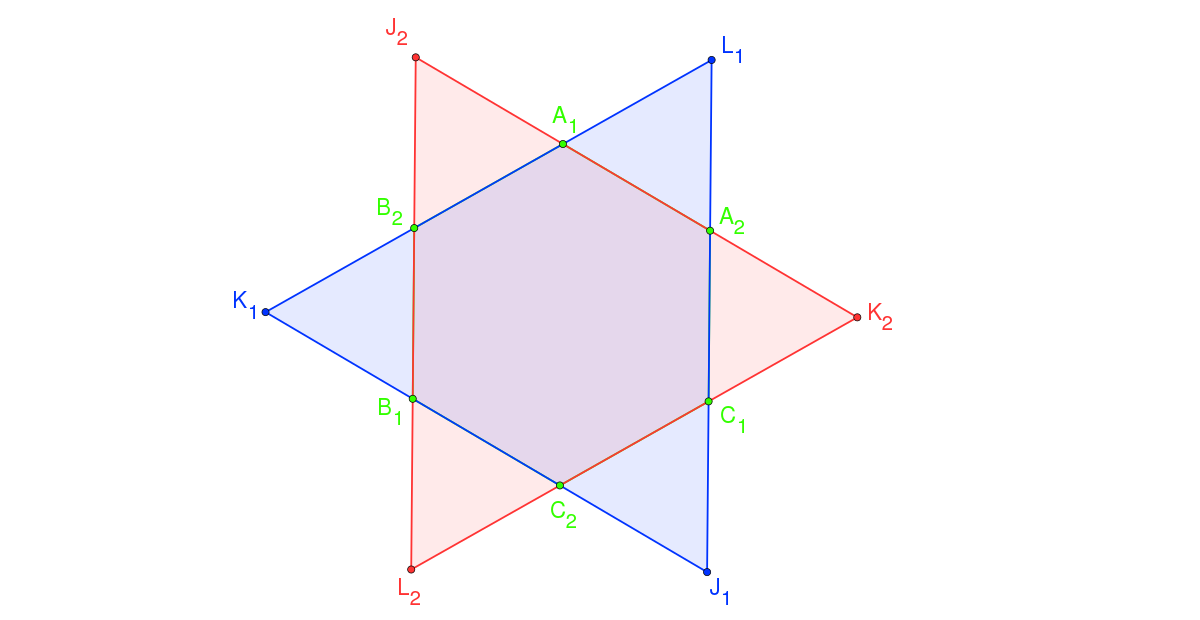
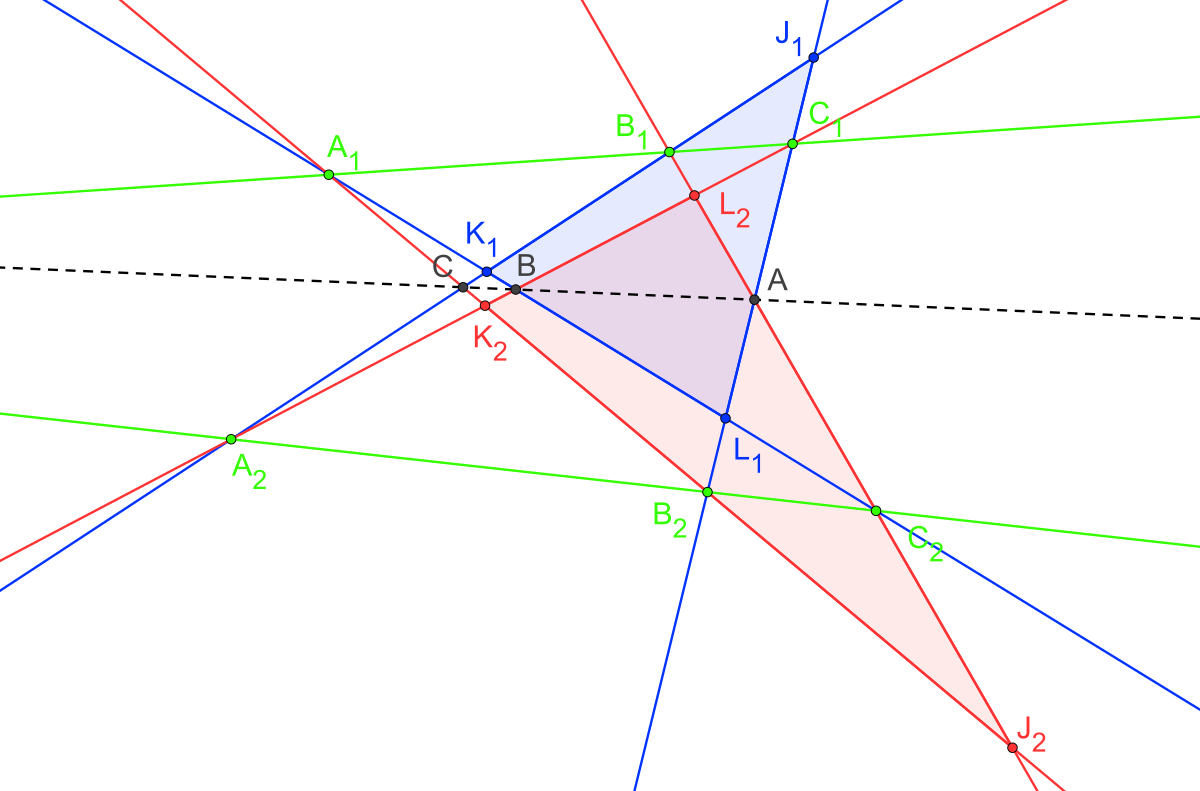
On peut illustrer sur une autre configuration, avec quelle facilité le circuit hexagonal permet de trouver les deux triangles de référence. Définissons cette fois-ci :

• A comme l'intersection de (A₁B₂) avec (C₁C₂)
• B comme l'intersection de (A₁A₂) avec (B₁C₂)
• C comme l'intersection de (C₁A₂) avec (B₁B₂)

Le circuit hexagonal est alors A₁, A₂, C₁, C₂, B₁ et B₂ et les deux triangles de référence sont alors :

• le triangle J₁K₁L₁ (en bleu sur la figure) dont les sommets sont les intersections des droites (A₁B₂), (B₁C₂) et (A₂C₁),
• le triangle J₂K₂L₂ (en rouge sur la figure) dont les sommets sont les intersections des droites (A₂B₁), (B₂C₁) et (A₁C₂).

Circuit hexagonal et triangles de référence d'une autre configuration

Démonstration du théorème de Pappus à l'aide de Ménélaüs sur une autre configuration