Théorème de Jordan - Définition

Introduction

La courbe de Jordan (en noir) divise le plan en deux régions : un « intérieur » (en bleu) et un « extérieur » (en rose). Ce résultat porte le nom de théorème de Jordan.

En mathématiques, le théorème de Jordan est un théorème de topologie plane. Il est célèbre par le caractère apparemment intuitif de son énoncé et la difficulté de sa démonstration. « En fait, il n'y a pratiquement aucun autre théorème qui apparaisse aussi évident en apparence que n'importe quel axiome de géométrie élémentaire et dont la preuve est tout sauf évidente » précise M. Dostal à son sujet.

Si, à l'aide d'un crayon, on dessine une ligne continue (on ne lève pas le crayon) qui ne se croise pas et qui termine là où elle commence, la zone de la feuille non dessinée se décompose en deux parties, l'intérieur de la figure, qui est borné, et l'extérieur, qui ne le serait pas si la feuille ne l'était pas. Pour s'en rendre compte, il suffit de découper la feuille à l'emplacement de la ligne, on obtient bien deux morceaux.

Ce théorème est l'un des piliers de la topologie du plan, qui correspond à l'étude des transformations, sans arrachage ni recollement (le plan est considéré comme formé d'une baudruche infiniment souple mais indéchirable). Une manière ludique d'en comprendre son intérêt est l'énigme des trois maisons. On considère dans le plan trois maisons représentées par des points et trois fournisseurs d'eau, de gaz et d'électricité. L'objectif est de relier chaque maison aux trois fournisseurs par des lignes, sans que deux de ces lignes ne se croisent. Le théorème de Jordan permet de montrer que c'est impossible. Il est utilisé pour mieux comprendre les équations différentielles. On le trouve encore en analyse complexe, à travers la théorie des résidus, et en géométrie différentielle.

Bernard Bolzano est le premier mathématicien à considérer le résultat de l'article comme une question mathématique. Il formalise les définitions à l'origine de la démonstration. Camille Jordan rédige la première démonstration, qui reste d'actualité de par la simplicité des outils mathématiques utilisés. Dans son Cours d'analyse, Jordan présente la partie facile de la preuve sous forme d'un exercice dont la solution n'est pas rédigée. Ceci amène souvent à considérer la démonstration de Veblen, plus tardive, comme la première preuve complète.

Préambule

Énoncé

Un archipel est constitué de plusieurs composantes connexes (les îles) : il n'est pas possible de passer à pied sec d'une île à l'autre. La frontière (au sens mathématique) d'une île est son littoral : un lacet simple.

Une courbe de Jordan dans un plan affine réel est une courbe fermée simple, on parle aussi de lacet simple. Autrement dit, une courbe de Jordan est l'image d'une application φ, continue et injective d'un cercle vers un plan ou encore une bijection du cercle dans son image. Comme le cercle est compact, l'image par φ d'un fermé est un fermé, ce qui montre que sa réciproque est continue, on parle d'homéomorphisme sur son image. Par abus, et comme souvent, dans cet article les termes de courbe fermée simple et de lacet simple, désignent à la fois l'application φ et son image. Certains auteurs plus précis considèrent que le terme de courbe fermée simple désigne uniquement l'image de l'application φ et que le terme de courbe fermée est synonyme d'arc paramétré défini sur un segment.

Intuitivement, un connexe est un espace topologique d'un seul tenant. Les connexes du théorème ont une propriété particulière : on peut aller d'un point à un autre d'un même connexe en empruntant un chemin qui ne quitte pas le connexe, on parle alors de connexe par arcs. Une composante connexe est un connexe maximal pour l'inclusion. Autrement dit, si l'on ajoute une partie quelconque du complémentaire à une composante, l'ensemble n'est plus connexe. Le terme de frontière correspond à l'idée intuitive que l'on s'en fait. Tout disque de rayon non nul et de centre un point de la frontière, contient des points d'au moins deux composantes connexes.

Le théorème dit de Jordan s'énonce ainsi :

Difficulté du théorème

Il n'est pas toujours intuitivement évident de savoir si un point se situe dans la zone intérieure.

La frontière d'un flocon de Koch est définie par une courbe continue et nulle part dérivable.

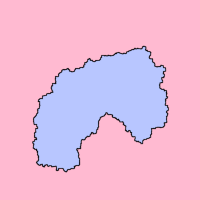
L'approche intuitive est trompeuse, on imagine généralement des lacets simples un peu rudimentaires, relativement proche d'un cercle, à l'image de la figure introductive de l'article. Cependant, une courbe de Jordan peut être beaucoup plus complexe. La figure de gauche illustre un exemple disposant de nombreux enroulements. Savoir si le point rouge est ou non dans à l'intérieur du lacet n'est pas aussi facile qu'on aurait pu le penser de prime abord.

Un lacet simple peut être vu comme un élastique circulaire déformé à volonté, de telle manière à ce que deux points distincts ne se touchent jamais. L'élastique est supposé être infiniment élastique. Autrement dit, il peut acquérir une longueur infinie. Cela revient à dire que le dessinateur de l'introduction est supposé être capable de tracer une ligne infiniment rapidement avec une précision infinie. Sur une idée de Karl Weierstrass, le mathématicien Helge von Koch trouve un lacet simple nulle part dérivable. Le motif qui le constitue est répété à l'infini, un peu comme un flocon de neige dont les branches supporteraient d'autres branches plus petites qui en contiendraient encore d'autres... Cette construction correspond à une géométrie fractale et la dimension de la frontière est strictement plus grande que 1. Savoir s'il existe un chemin reliant deux points profondément imbriqués dans les petites radicelles de la figure n'est plus aussi intuitif que pourrait le laisser penser une lecture rapide de l'énoncé .

D. Leborgne indique que : « Ce qui est remarquable [...] est, d'une part l'extrême simplicité (apparente) des énoncés, et, d'autre part, la difficulté importante de leur démonstration. ». La grande généralité du théorème, c'est-à-dire le fait qu'il soit vrai sans supposer d'hypothèse de régularité comme la dérivabilité ou au moins le caractère lipschitzien de la courbe de Jordan, complexifie en réalité plus l'énoncé qu'elle ne le simplifie.

Usages

L'énigme des trois maisons

Un bouchon posé sur un étang parcouru par un courant indépendant du temps finit soit par s'immobiliser, soit par parcourir indéfiniment une boucle. Ce théorème est une conséquence du résultat de l'article.

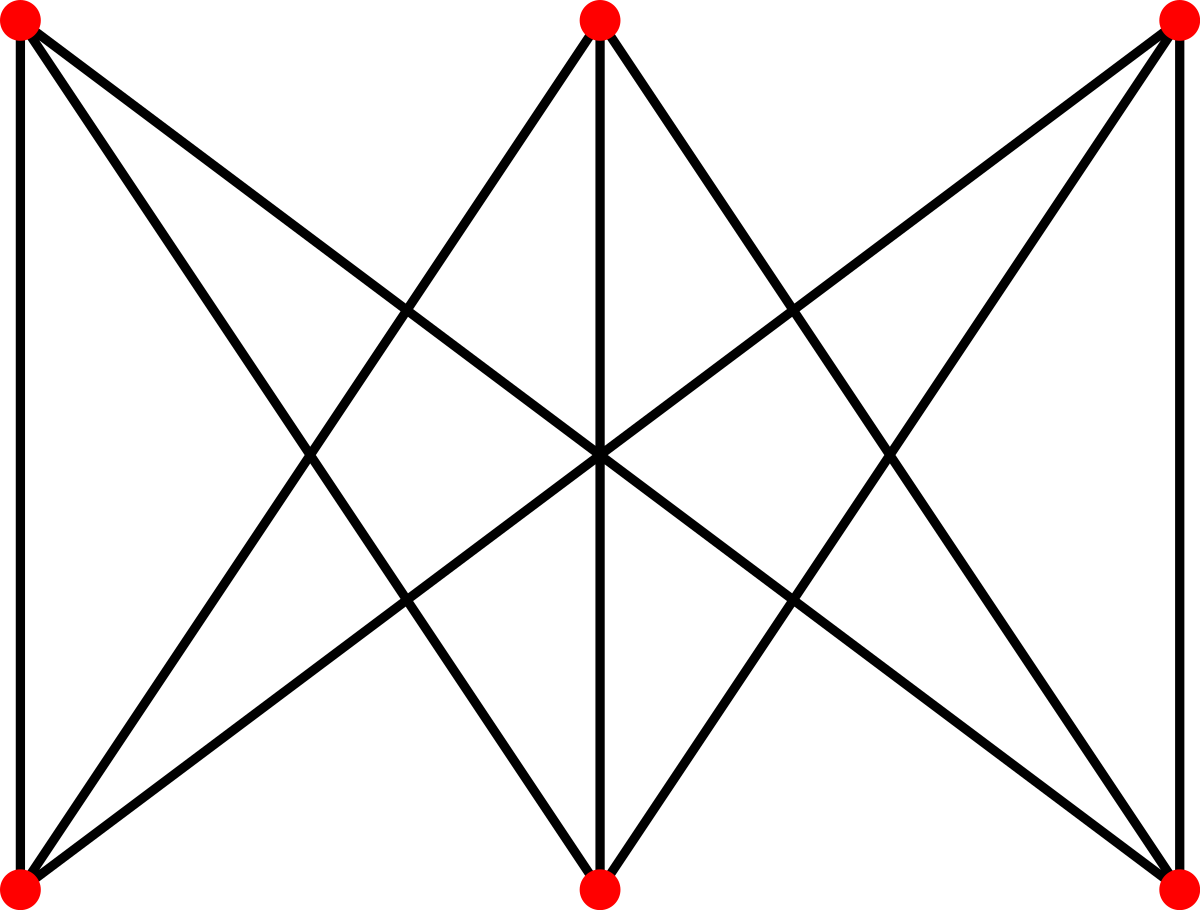
Le théorème de Jordan intervient dans des branches fort différentes des mathématiques. Son domaine naturel est la topologie. Une manière d'illustrer son usage est l'énigme des trois maisons, illustrée sur la figure de gauche et posée pour la première fois par H. E. Dudeney en 1917. Comment relier chacun des trois points rouges du bas à chacun des trois points rouges du haut de telle manière à ce que les liens ne se chevauchent pas ? Le théorème de Jordan permet de montrer qu'il n'existe pas de solution. De manière moins anecdotique, le résultat de l'article est la cheville ouvrière de la démonstration du théorème de Kuratowski, le résultat clé des graphes planaires.

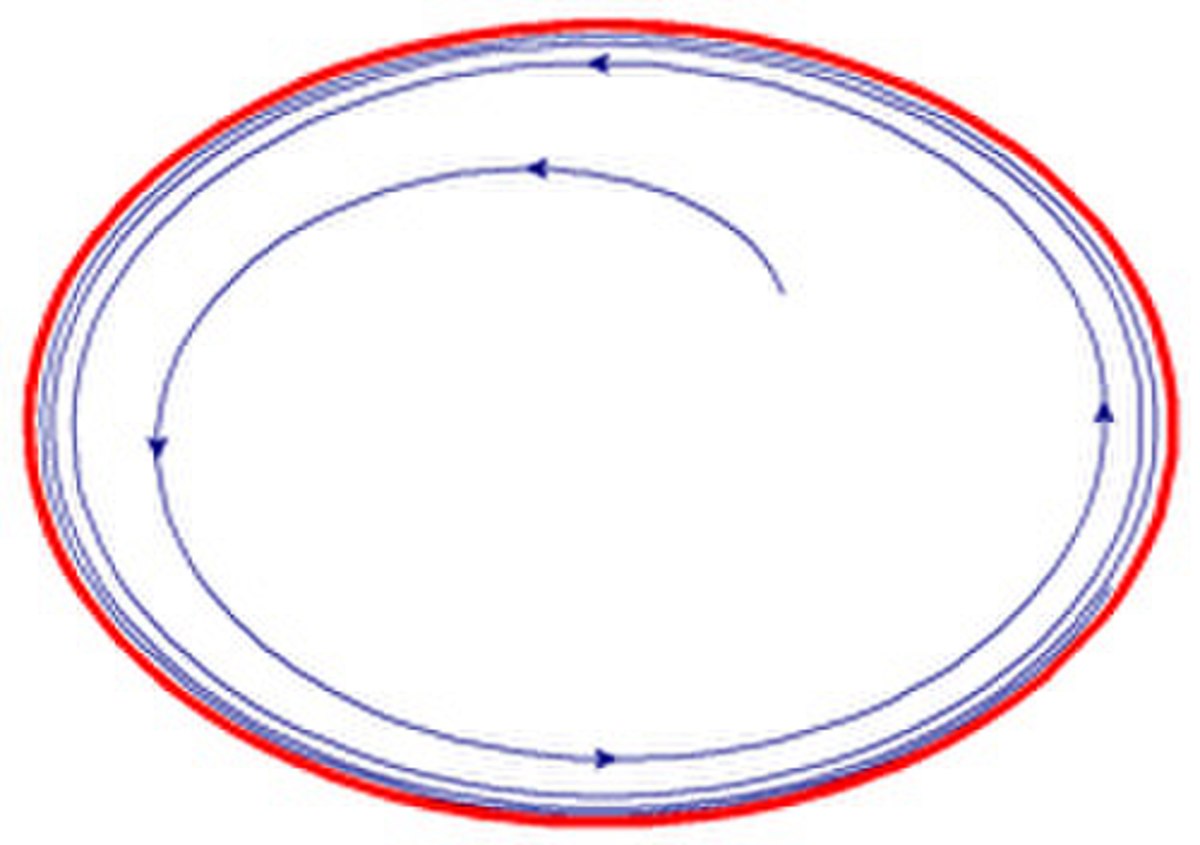
Un usage plus classique est associé à une meilleure compréhension d'une famille d'équations différentielles. Elle correspond à celles de la forme x' = f(x) où f est une fonction suffisamment régulière de la variable réelle dans le plan. On peut l'imaginer comme l'équation d'un bouchon sur un étang parcouru d'un courant modélisé par la fonction f. Si une solution est bornée, elle ne peut quitter un disque de rayon suffisamment grand. Le théorème de Cauchy-Lipschitz indique que la solution ne peut passer deux fois par le même point, cette contrainte lui impose soit de converger vers un point, soit vers un cycle limite. Autrement dit, le bouchon finit par s'immobiliser ou tourner indéfiniment autour d'un lacet de Jordan. Ce résultat est connu sous le nom de théorème de Poincaré-Bendixson.

L'analyse complexe étudie les fonctions de la variable complexe à valeurs dans les complexes. Si la fonction, notée ici f, est dérivable (au sens complexe) elle est développable en série entière en chaque point de son domaine de définition et le rayon de convergence de cette série, en un point du domaine, n'est jamais nul. Une telle fonction est dite méromorphe. Elle peut comporter des singularités, un peu de même nature que les zéros du dénominateur des fractions rationnelles. Soit γ un lacet simple du plan complexe, ne passant par aucun zéro de f ni aucune singularité. Le lacet γof fait autant de fois le tour des racines que l'intérieur du lacet contient de zéros. La valeur de l'intégrale curviligne du lacet γof est intimement associée aux singularités qui se trouvent à l'intérieur du lacet γ, ce résultat est connu sous le nom de théorème des résidus. Pour ces différentes raisons, il n'est guère possible d'écrire un livre sur l'analyse complexe sans présenter le théorème de Jordan.

La géométrie différentielle n'est pas en reste. Il permet d'orienter tout lacet simple et montre que la courbure totale d'un lacet simple dérivable est égale à 2π. Ces différentes raisons font écrire à D. Leborgne que le résultat de l'article est l'un des : « grands théorèmes concernant la topologie des espaces de dimension finie. ».