Théorème de Jordan - Définition

Extensions et approfondissements

Le théorème de Jordan-Brouwer

Démontré par L. E. J. Brouwer en 1912, cet énoncé généralise sans hypothèse supplémentaire le théorème de Jordan en dimensions supérieures :

Théorème de Jordan-Schönflies

Le théorème de Jordan-Schönflies généralise le résultat de l'article.

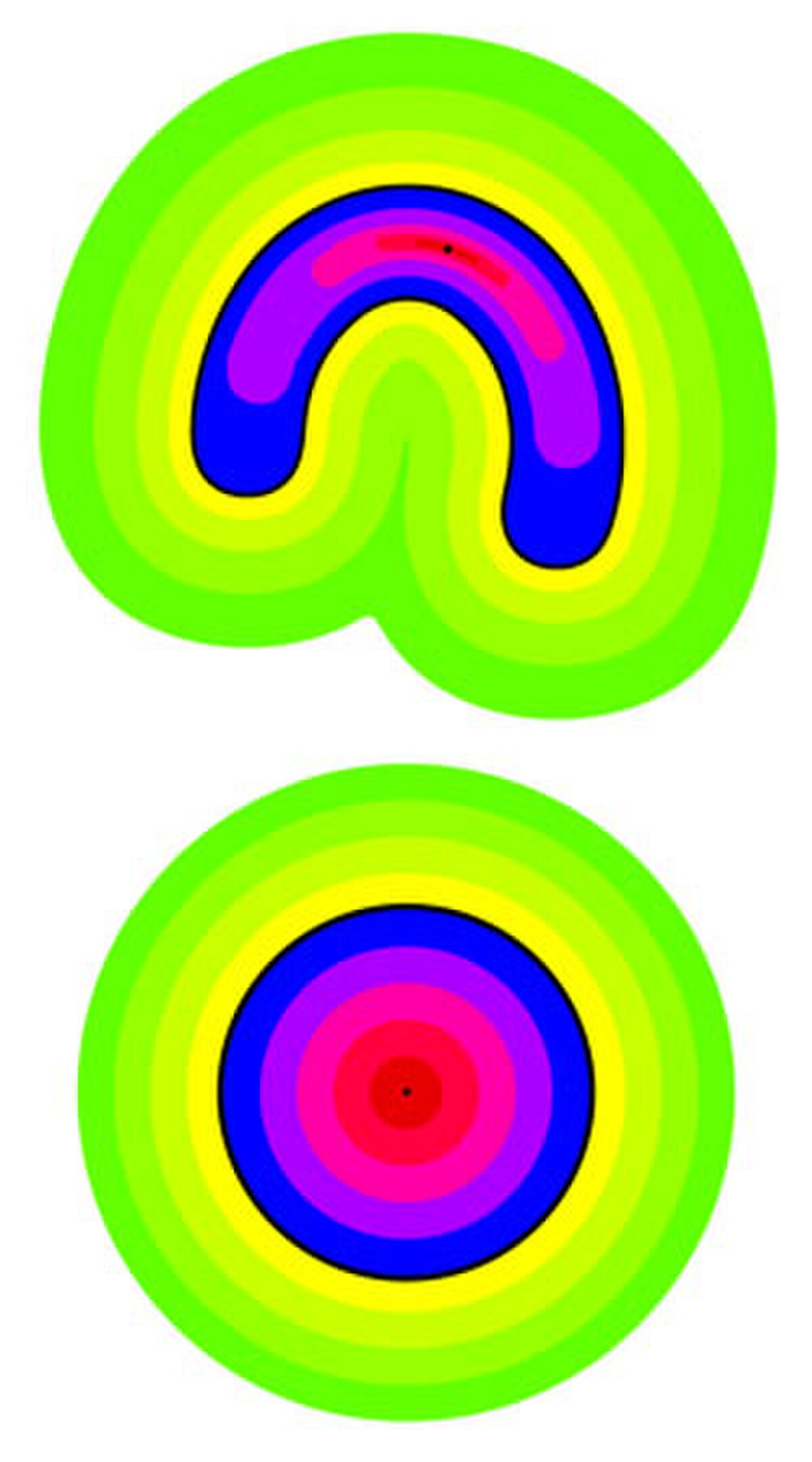
Par définition, une courbe de Jordan est un cercle déformé. Autrement dit, il existe un homéomorphisme entre un cercle et une courbe de Jordan. Pour le complémentaire de cette courbe dans le plan, le théorème de l'article indique juste qu'il est composé de deux composantes connexes, l'une bornée l'autre non. Ceci amène naturellement la question de la nature topologique de ces deux composantes connexes.

La figure de droite laisse penser que l'intérieur correspond aussi à un disque ouvert déformé, c'est-à-dire qu'il existe un homéomorphisme du disque fermée dans la courbe de Jordan et son intérieur. Sur la figure de droite, cet homéomorphisme fait correspondre la frontière du fer à cheval, correspondant à la courbe de Jordan au cercle noir du bas. Il fait aussi correspondre chaque zone de couleur de l'intérieur du fer à cheval avec la zone de même couleur dans la figure circulaire du bas. Ce théorème, démontré par Arthur Schönflies en 1906, complète l'information fournie par le théorème de Jordan, en précisant la topologie des régions délimitées par la courbe :

A l'aide d'une inversion, il est simple de vérifier que le théorème est aussi vrai sur la composante connexe non bornée. Autrement dit, la zone illustrée sur la figure de droite en jaune et vert à l'extérieur du lacet correspond à une déformation de la zone aussi illustrée en jaune et vert à l'extérieur du cercle. La compacité de la courbe de Jordan montre qu'il est possible de recoller les deux homéomorphismes. On en déduit qu'il existe un homéomorphisme du plan dans lui même qui a pour image du cercle C celle de la courbe de Jordan.

Théorème de Schönflies généralisé

La sphère à cornes d'Alexander est homéomorphe à la sphère euclidienne.

Cherchant à étendre le théorème de Schönflies en dimensions supérieures, le topologue J. W. Alexander découvre en 1924 un contre-exemple inattendu en dimension 3 : la sphère à cornes d'Alexander. Le théorème de Jordan-Schönflies ne se généralise pas simplement en dimensions supérieures, et il peut même arriver qu'un ensemble homéomorphe à une sphère dans R³ limite un ouvert borné dont la topologie est sensiblement plus compliquée que celle d'une boule.

Cette sphère à corne d'Alexander est illustrée sur la figure de droite. Étonnamment, elle est simplement connexe, c'est-à-dire que tout lacet est homotope à un point, ou encore se rétracte continument en un point, à la différence d'un tore ou d'un cercle. Plus on avance dans la structure, plus elle devient fine. Autrement dit, elle n'est pas différentiable.

Cette remarque rend possible une généralisation du théorème de Schönflies en dimensions supérieures, à condition de faire une hypothèse supplémentaire de régularité sur le plongement considéré de la sphère Sⁿ, mais il faut attendre sensiblement plus longtemps pour que cela soit démontré. Le théorème de Schönflies généralisé, prouvé par Morton Brown et Barry Mazur en 1960, étend le théorème de Jordan-Schönflies en dimension quelconque, sous une hypothèse technique sur l'homéomorphisme X est un difféomorphisme. Cette condition est remplie notamment si on suppose que l'image de la sphère est une variété différentiable ou linéaire par morceaux.