Théorème de Jordan - Définition

Principes de démonstrations

Par l'orientation

Un ruban de Möbius n'est pas orientable.

L'orientation est à la base d'une méthode de démonstration du théorème de Jordan pour les courbes continument dérivables.

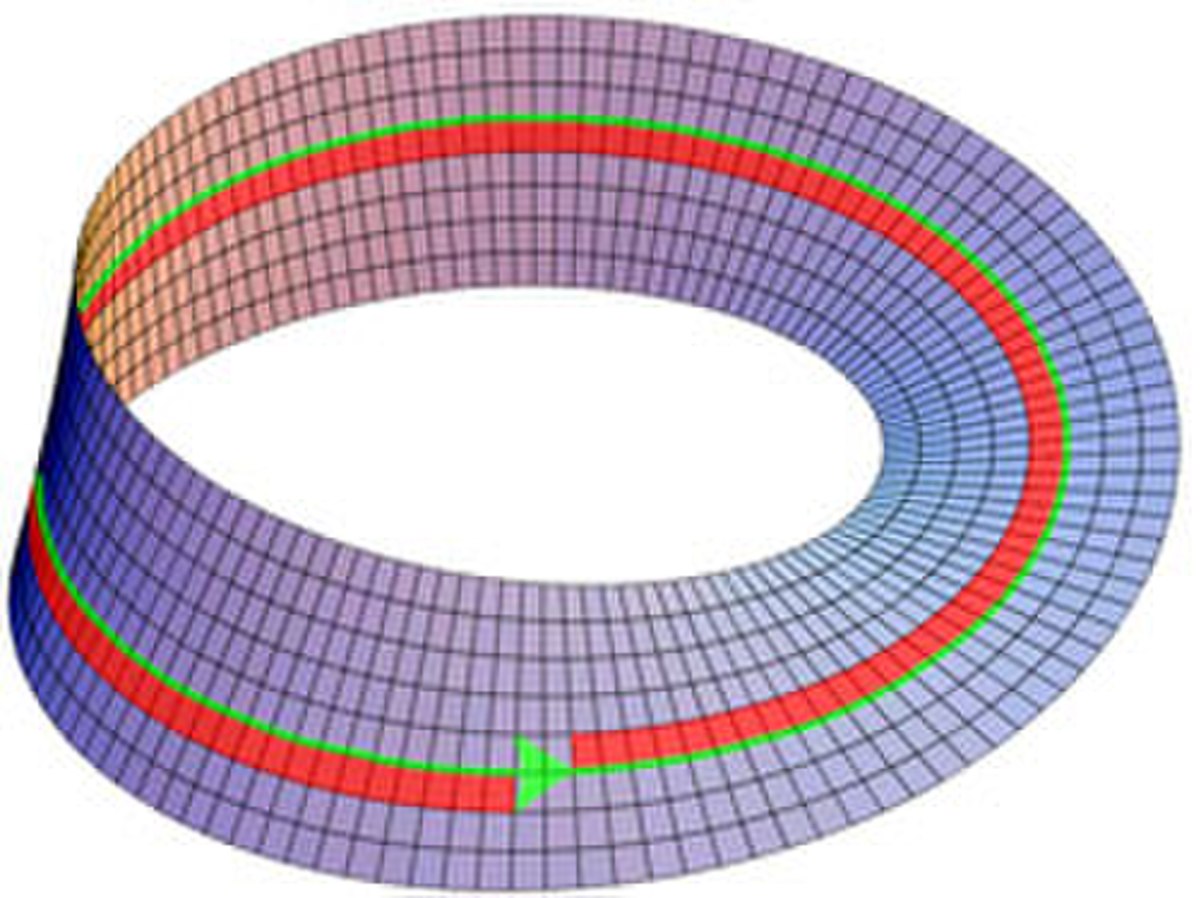
Une méthode pour trouver des idées de démonstration du théorème est la recherche de contre-exemple. La figure de gauche représente un ruban de Möbius. S'il est découpé selon la ligne verte, on obtient un connexe, correspondant à une portion de cylindre deux fois plus longue et deux fois moins large que le ruban original. La ligne verte correspond à un contre-exemple du résultat de l'article et le théorème de Jordan est faux sur le ruban de Möbius.

Une spécificité de ce ruban est d'être non orientable. Pour s'en rendre compte, le plus simple est de parcourir la courbe dans le sens de la flèche et de peindre en rouge le côté gauche. Après un tour, le côté peint en rouge est devenu le droit, ce qui indique que le côté gauche est devenu le droit, ou encore que sur une telle géométrie les mots droite et gauche n'ont pas de sens global.

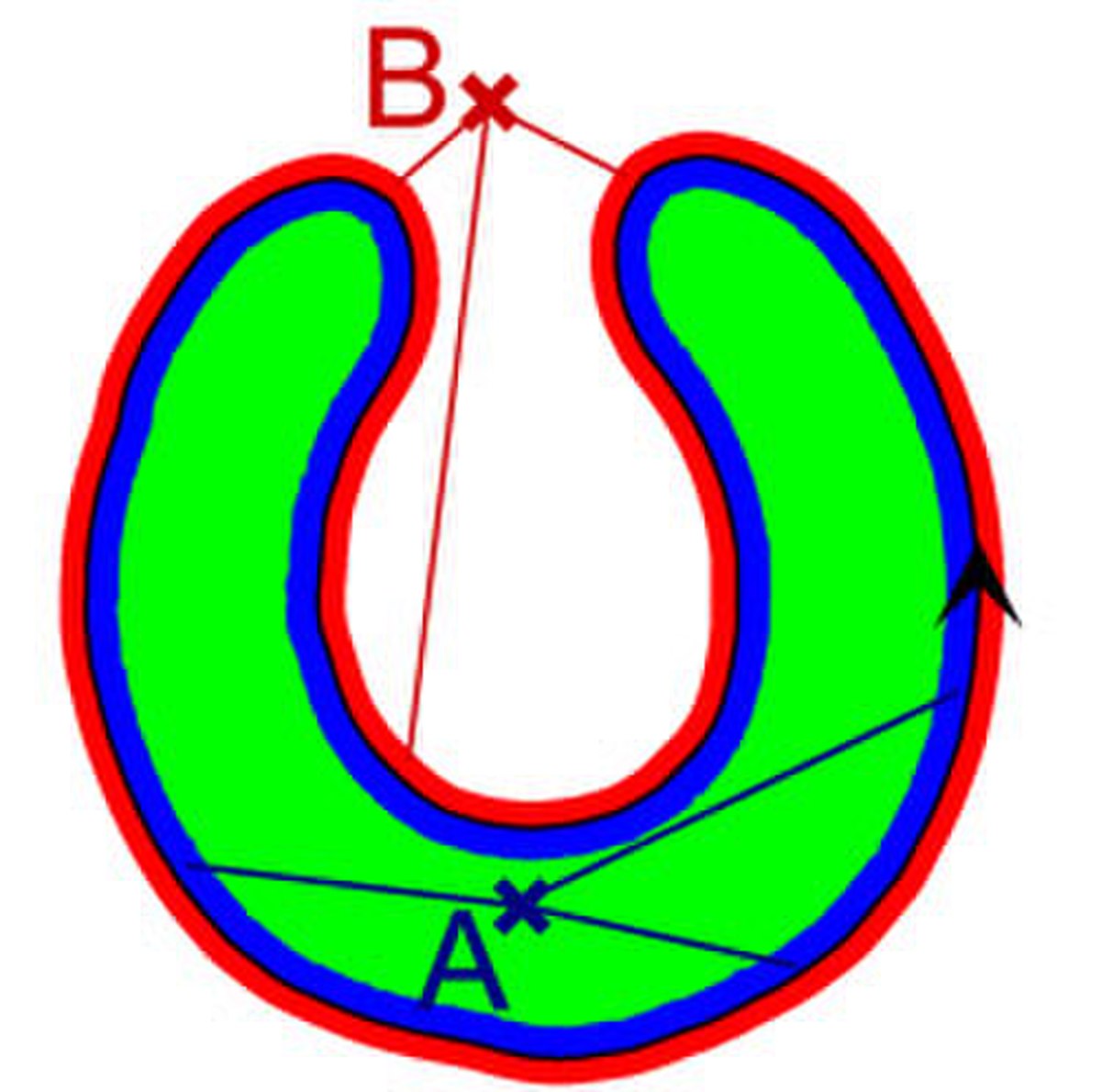
Cette remarque est la source d'une démonstration. On considère une courbe de Jordan, continument dérivable, à valeurs dans un plan et illustrée en noir (entre les zones bleue et rouge) sur la figure de droite. Son sens (une courbe, continument dérivable et définie dans le plan, possède toujours une orientation) est décrit par la flèche noire. On considère la zone en rouge immédiatement à droite de la courbe et la zone en bleu immédiatement à gauche. Il est assez simple de montrer que les zones rouge et bleue sont des connexes par arcs, si les bandes sont choisies suffisamment étroites. On considère un point P à l'extérieur de la courbe et une demi droite reliant P et la courbe de Jordan. Si cette demi-droite intersecte d'abord la zone bleue, elle est dans la composante connexe bleue, car l'union de la zone bleu et de la demi-droite est connexe par arcs. Sinon, la demi-droite intersecte d'abord la zone rouge et elle est dans la composante extérieure. On en déduit qu'il existe au plus deux composantes connexes.

Il reste encore à montrer que l'intérieur et l'extérieur ne sont pas connexes. Soit deux points dans la même composante connexe et tel que le premier est dans l'intérieur. Pour chacun des deux points, il existe un arc reliant le point à un point d'une zone choisie bleue pour le premier et de couleur indéfinie pour le second. Les deux extrémités sont dans les zones bleue ou rouge. On relie les deux extrémité par un arc qui ne croise pas la courbe de Jordan et qui ne quitte pas les zones bleue et rouge (obtenu par exemple en projetant un arc quelconque qui relie les deux extrémités sur les zones bleue et rouge), cet arc ne peut croiser la courbe de Jordan, elle reste donc toujours du côté bleu. Cela signifie que toute demi-droite d'extrémités A, située à l'intérieur de la courbe et un point de la courbe rencontre d'abord la zone bleue, et que si B est située à l'extérieur, la demi-droite équivalente rencontre d'abord la zone rouge. Cela montre encore qu'il existe exactement deux composantes connexes.

Cette remarque conclut la démonstration pour les courbes de Jordan continument dérivables. La partie la plus délicate reste à montrer que, comme toute courbe de Jordan est proche d'un lacet continument dérivable, la propriété est encore vraie pour les courbes non dérivables.

Par l'analyse complexe

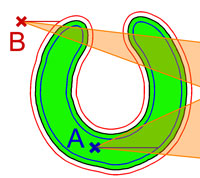
Une preuve ne fait appel qu'à l'analyse complexe. On considère que la courbe de Jordan γ (représenté en noir sur la figure de droite) est à valeurs dans C, l'ensemble des nombres complexes. On suppose encore que γ est continument dérivable et qu'elle dispose d'une abscisse curviligne, c'est-à-dire que le module de la dérivée est toujours égale à 1. On considère ε un réel strictement positif, suffisamment petit et les deux courbes γ₊ en rouge et γ_- en bleu définies par :

Ces deux courbes jouent le même rôle que l'orientation du paragraphe précédent. Un point A qui rencontre d'abord la courbe γ₊ est dans la composante connexe de γ₊ et un point B qui rencontre d'abord la courbe γ_- est dans celle de γ_-. Par l'analyse, on démontre ainsi qu'il existe au plus deux composantes connexes.

La suite du raisonnement diffère du paragraphe précédent. On suppose maintenant que le point A est une source de lumière qui en produit une quantité égale à 1. Quand la lumière se diffuse dans le plan (à la différence de la physique, on suppose ici que l'univers est de dimension deux et non pas trois), elle s'étale sur un cercle. Un point du cercle à une distance r de A reçoit donc une quantité de lumière égale à 1/2.πr. Comme toute la lumière finit par traverser et sortir de la courbe de Jordan, on dispose de l'égalité :

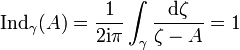
Cette valeur est appelée indice du point A relativement au lacet γ. Le même calcul, si la source est maintenant le point B donne 0. En effet, comme le point B est à l'extérieur du lacet, toute la lumière qui entre finit par sortir. Ce calcul d'indice montre l'existence de deux composantes connexes. En effet, sur le complémentaire du support de la courbe de Jordan γ, la fonction qui à un point associe son indice est continue. Son image n'est pas connexe car égale à {0, 1}, l'ensemble de départ ne peut pas l'être non plus.

Par le théorème du point fixe de Brouwer

Le tore ne vérifie ni le théorème de Jordan, ni celui du point fixe de Brouwer.

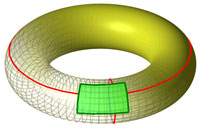
Une autre figure qui ne vérifie pas le théorème de Jordan est le tore. Cette figure est un peu équivalente à la surface d'un pneu. Le plus grand cercle que l'on peut dessiner sur un tore est une courbe de Jordan, mais elle ne sépare pas la figure en deux composantes connexes. Une fois encore, il existe un théorème valable sur un rectangle (une courbe de Jordan sur un plan est bornée, il existe donc un rectangle dont l'intérieur la contient) et faux sur un tore. Toute application continue définie sur un rectangle et son intérieur, à valeurs dans la même zone, admet un point fixe, ce résultat est connu sous le nom de théorème du point fixe de Brouwer. La rotation d'un quart de tour par rapport à l'axe du tore ne laisse invariant aucun des points du tore. Cette géométrie ne vérifie donc pas non plus le théorème du point fixe de Brouwer.

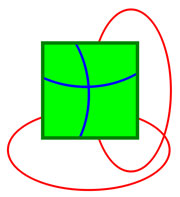
Une conséquence du théorème de Brouwer est qu'un chemin qui part de l'arête supérieure d'un rectangle pour rejoindre l'arête inférieure, sans quitter l'intérieur du rectangle, croise tout chemin qui part de l'arête de gauche pour rejoindre l'arête de droite, aussi sans quitter l'intérieur du rectangle. Ce résultat est illustré sur la figure de gauche avec les deux chemins bleus. Si les chemins sont tout deux à l'extérieur du rectangle, le résultat est encore vrai. Il est illustré sur la figure de gauche par les chemins rouges. La figure de droite montre que ce résultat n'est pas valide sur un tore, les deux chemins rouges ne se croisent pas.

Cette remarque est à l'origine de la preuve détaillée du théorème de Jordan contenue dans cet article.