Théorème de Carathéodory (géométrie) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le théorème de Carathéodory est un théorème de géométrie relatif aux enveloppes convexes dans le contexte des espaces affines de dimension finie.
Énoncé
Le théorème, établi par le mathématicien grec Constantin Carathéodory affirme que :
Théorème — Dans un espace affine de dimension n, l'enveloppe convexe d'un sous-ensemble A est l'ensemble des barycentres à coefficients positifs ou nuls de familles de n + 1 points de A.
Corollaire : un résultat de compacité
Corollaire — Dans un espace affine de dimension finie, l'enveloppe convexe d'un compact est compacte.
En effet, soit


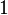


Preuves
La preuve usuelle
Notons Conv(A) l'enveloppe convexe de A, et Γ l'ensemble des barycentres à coefficients positifs ou nuls d'au plus n + 1 points de A. On veut montrer l'égalité de ces deux ensembles.
L'inclusion



Soit


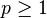
Si




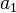


En posant

 ,
,

 ,
,


Choisissons k tel que :  et remplaçons, dans l'expression de x, le point ak par
et remplaçons, dans l'expression de x, le point ak par

Par "associativité du barycentre" on obtient



Si  , alors
, alors




x est donc barycentre à coefficients positifs ou nuls de p éléments de A.
Une preuve comme conséquence du théorème de Helly
Les possibilités de déduire l'un de l'autre les théorèmes de Helly et de Caratheodory, le premier parlant d'intersections finies de convexes, qu'on peut ramener au seul problème d'intersections finies de demi-espaces, tandis que le second parle d'enveloppe convexe d'un nombre fini de points sont fort instructives pour illustrer les techniques de dualité en géométrie convexe, qui échangent points et demi-espaces. Deux preuves du théorème de Helly dans l'article qui lui est consacré en font une conséquence de Carathéodory, dont une fort instructive via le lemme de Farkas ; aller dans l'autre sens (tirer Carathéodory de Helly) est plutôt plus facile encore, et on peut se borner à utiliser un théorème de Gordan d'esprit voisin du lemme de Farkas, mais de démonstration nettement plus aisée.
Soit x un point de l'enveloppe convexe de A. Quitte à translater la figure, on peut supposer que x = 0. Il existe donc une famille finie de points de A, soit



 .
.
Le théorème de Gordan (en réalité le sens évident de celui-ci) assure que les demi-espaces Rj (j variant entre 1 et k) ont une intersection vide. Le théorème de Helly assure à son tour qu'il en existe une sous-famille avec seulement d + 1 membres qui a à son tour une intersection vide. Le sens plus significatif du théorème de Gordan permet alors de conclure que les d + 1 points aj correspondant à cette liste ont à leur tour 0 dans leur enveloppe convexe.