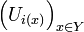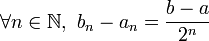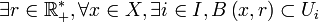Théorème de Bolzano-Weierstrass - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En topologie des espaces métriques, le théorème de Bolzano-Weierstrass donne une caractérisation séquentielle des espaces compacts. Il tire son nom des mathématiciens Bernard Bolzano et Karl Weierstrass.
Énoncé du théorème
Un espace métrique
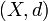
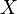
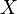
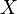
Cet énoncé peut se décomposer en :
- (sens direct) Dans un espace compact (non nécessairement métrisable), toute suite admet une valeur d'adhérence.
- (valeur d'adhérence dans un métrique) Dans tout espace topologique, si un élément
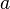
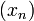
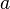
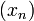
- (sens réciproque) Si
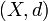
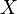
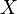
Énoncé dans le cas réel
De toute suite réelle bornée, on peut extraire une sous-suite convergente.
Pour montrer cette propriété, il suffit de remarquer que les intervalles fermés bornés de

Soit
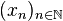

-
- 1) Construction de deux suites
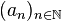
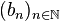
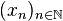
-
- 2) Construction de la suite extraite.
- 1) Construction de deux suites
- 1) Construction par dichotomie des suites
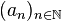
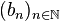
On définit a0 par a0 = a et b0 par b0 = b.
Pour tout entier naturel n, si l'intervalle
![\left[ a_n , \frac{a_n+b_n}{2} \right]](https://static.techno-science.net/illustration/Definitions/autres/1/1de141ae0cc69c56e48b90c7dbaa6d50_ed97a4d91fd47b1d8c592602f2aaad78.png)
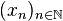
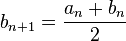
Sinon, l'intervalle
![\left[ \frac{a_n+b_n}{2},b_n \right]](https://static.techno-science.net/illustration/Definitions/autres/3/398f5c5488620d8b1749975da22d00d5_8176c5d12051bd19eb4df7205c9fda51.png)
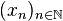
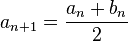
On vérifie que ces deux suites ainsi construite sont adjacentes et que l'intervalle [a,b] contient une infinité de termes de la suite
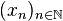
- 2) Construction par récurrence de la suite extraite convergente
Cela revient à dire que nous cherchons une fonction



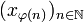
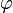
Posons
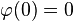

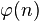
![x_m\in \left[ a_{n+1},b_{n+1} \right]](https://static.techno-science.net/illustration/Definitions/autres/1/1d5a834ed67d58283932c507bb3870c0_51cc6ece540320c67e1c49cdc9c1e6ef.png)
![\left[ a_{n+1}\ ,b_{n+1}\ \right]](https://static.techno-science.net/illustration/Definitions/autres/a/afcb3d55f5d8f2dd09bb975887ed1b72_27101ff6ee5152de2a5ebcd41617d627.png)
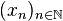
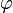
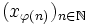
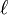
Démonstration
Sens direct
On suppose que
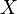
Soit
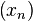
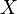
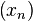
Notons
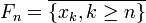
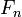
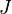
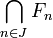
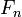
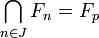
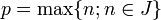
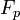
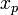
Sens réciproque
Dans cette démonstration, on qualifiera de séquentiellement compact un espace métrique dans lequel toute suite admet une sous-suite convergente.
Premier lemme (nombres de Lebesgue d'un recouvrement)
Si
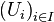
c'est-à-dire qu'il existe des  tels que toute boule ouverte de rayon
tels que toute boule ouverte de rayon

Par l'absurde. On suppose
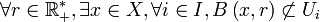
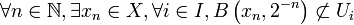
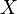
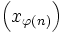
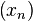
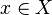
Comme les
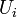
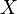
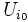
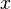
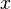
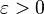 .
.
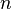
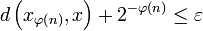
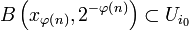
Deuxième lemme (précompacité)
Si X est séquentiellement compact alors pour tout r > 0, X est recouvert par un nombre fini de boules de rayon r.
Par l'absurde. On nie le résultat, puis on construit une suite qui nous permettra de trouver une contradiction. On suppose donc que pour un certain r > 0, aucune union finie de boules de rayon r ne remplit X. Ceci permet de construire par récurrence une suite (xn) de points de X telle que pour tout n,
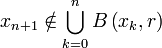
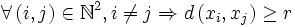
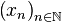
Fin de la démonstration du théorème
Supposons X séquentiellement compact et prouvons qu'il est compact. Soit
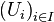
D'après le premier lemme, il existe r > 0 tel que
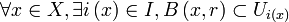
D'après le lemme de précompacité, il existe une partie finie Y de X telle que
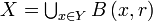
On en déduit alors que la sous-famille finie