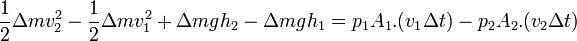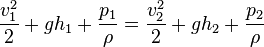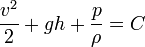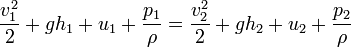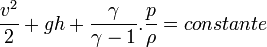Théorème de Bernoulli - Définition
La liste des auteurs de cet article est disponible ici.
Démonstrations
-
Équation de Bernoulli pour les fluides incompressibles L'équation de Bernoulli pour les fluides incompressibles peut être démontrée par intégration des équations d'Euler du mouvement, qui dans les hypothèses du théorème se ramènent à l'équation de Navier-Stokes. On peut également appliquer le principe de conservation de l'énergie le long d'une ligne de courant, en négligeant les effets thermiques, de viscosité, de compressibilité.
C'est ce second point de vue que l'on suit ici.
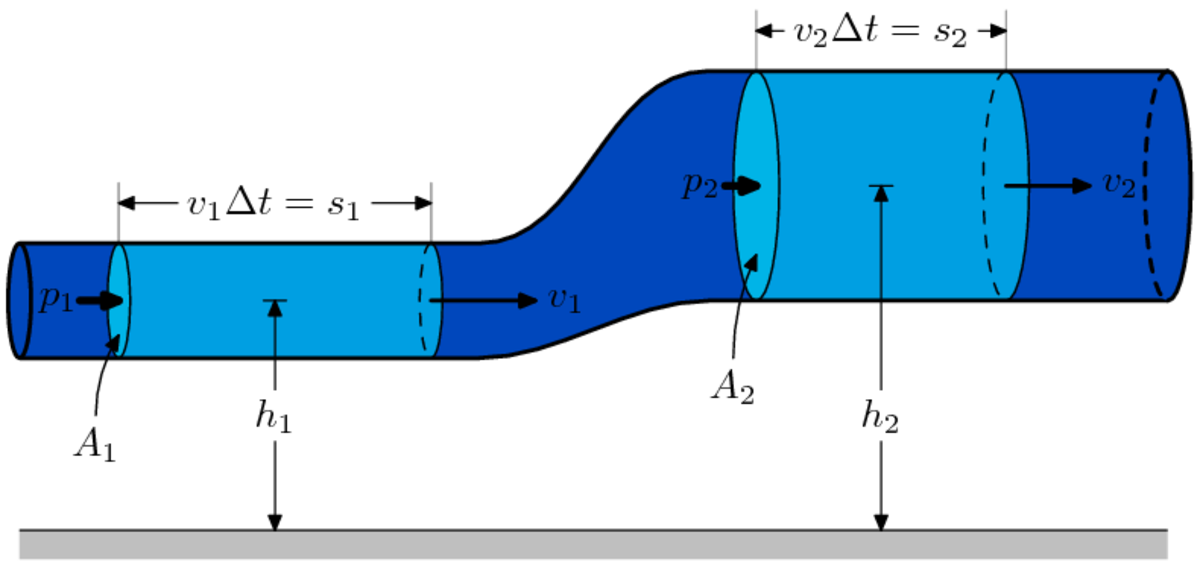Tube de courant du fluide. On indique les pressions (p), altitudes (h), vitesses (v), longueurs (s) et sections (A).Soit le système fermé contenu à l'instant t entre x1 et x2 et à t + Δt entre x1 + v1.Δt et x2 + v2.Δt.
Le fluide est incompressible, la masse Δm contenue entre x1 et x1 + v1.Δt doit être identique à la masse contenue entre x2 et x2 + v2.Δt.
Ce que l'on peut ramener ici à la conservation du débit massique : Δt.v1.A1.ρ = Δt.v2.A2.ρ.
Toutes les forces qui s'exercent (forces pressantes et poids) sont conservatives (il n'y a pas d'effet visqueux). On peut donc appliquer le théorème de conservation de l'énergie mécanique au système :
- ΔEpp + ΔEk = W
où
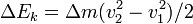
ΔEpp = Δmgh2 − Δmgh1 est la variation d'énergie potentielle de pesanteur du système.
W = p1A1.(v1Δt) − p2A2.(v2Δt) est le travail des forces de pressions.
Soit :
D'où, en divisant par Δm :
Et donc :
On peut remarquer que la démonstration est faite dans le contexte particulier d'un écoulement obéissant à la géométrie de la figure. Cependant, pour un écoulement quelconque en régime permanent, on pourra toujours définir au voisinage d'une ligne de courant une section sur laquelle la vitesse est homogène, et raisonner comme précédemment.
-
Équation de Bernoulli pour les fluides compressibles La démonstration est identique à celles pour les fluides compressibles : elle s'appuie sur la conservation du débit et de l'énergie. Mais on doit prendre en compte dans la variation d'énergie du système la variation d'énergie interne du fluide entre t et t + Δt.
La conservation de l'énergie appliquée au système devient alors :
D'où :
Si on note l'enthalpie spécifique ω, dans le cas d'un gaz parfait, on vérifie
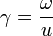
Comme
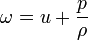
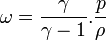
Donc dans ce cas,
-
Approche historique
La première formulation du théorème de Bernoulli apparaît dans Hydrodynamica - De viribus et motibus fluidorum commentarii de Daniel Bernoulli (première édition en 1738) [3] . Pour d'Alembert, ce texte est l'œuvre fondatrice de l'hydrodynamique en tant que discipline physique moderne.
Il est alors formulé comme un bilan macroscopique global et une méthode de calcul, dans le cadre de la résolution d'un problème technique : la détermination de la durée de vidange des vases munis d'un orifice.
La justification réside dans l'égalité de la montée potentielle et de la descente actuelle. Il s'agit d'une transposition aux fluides de la conservation des forces vives, déjà connue en mécanique, et qui est en fait l'ancêtre du principe de conservation de l'énergie dans le domaine de la physique classique.
C'est seulement en 1755, avec les travaux d'Euler, que le théorème apparaît sous la forme d'un bilan local plus proche des formulations contemporaines.
