Théorème d'inversion locale - Définition

Usages

Les usages du théorème d'inversion locale sont multiples et touchent différentes branches des mathématiques. L'une d'entre elle concerne la branche d'origine du théorème : la géométrie différentielle. Cet usage est pratiqué à l'aide d'un corollaire portant le nom de théorème des fonctions implicites. Il prend la forme d'un résultat équivalent à celui de l'article et le théorème d'inversion locale apparaît, soit sous sa forme d'origine, soit sous celle des fonctions implicites.

Sous cette forme, on l'utilise pour étudier les figures géométriques définies sous forme d'équations, illustrées par l'exemple suivant :

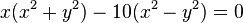
Si le terme de gauche est vu comme une fonction f de R² à valeurs dans R, la figure du plan étudié est l'intersection du graphe de la fonction f, illustré à droite, et du plan d'équation z = 0. De manière plus générale, une variété différentielle correspond à la généralisation de courbes ou surfaces régulières, en dimension quelconque. Il existe deux manières de les définir localement, à travers une équation, soit cartésienne, soit paramétrique. Le résultat de l'article montre l'équivalence de ces deux manières.

En calcul différentiel, le multiplicateur de Lagrange permet de trouver des extrema sous contrainte. Si U est un ouvert d'un espace euclidien, l'objectif est de trouver un extremum d'une fonction f définie sur les points x de U et à valeurs dans R vérifiant l'équation g(x) = 0, où g est une fonction à valeurs dans un autre espace euclidien.

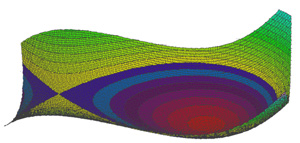
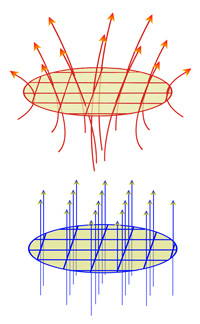
On le trouve encore dans les équations différentielles, où il est l'outil de démonstration du théorème du redressement d'un flot. Une équation différentielle explicite possède une forme équivalente à (1) x' = f(t, x). Si la fonction f est indépendante de t l'équation est dite autonome, la fonction est un champ de vecteur et les solutions de l'équation possèdent des graphes tangents en un point x au vecteur f(x), à l'image de la figure rouge et jaune, à gauche. Le théorème du redressement d'un flot montre que localement, l'équation différentielle est équivalente à celle ayant un champ constant, à l'image de la représentation bleue et jaune, encore à gauche.

Les exemples cités supposent généralement la dimension finie des espaces vectoriels considérés. Tel n'est pas toujours le cas. Une manière d'exprimer les solutions de l'équation (1) est de considérer le flot, c'est-à-dire la fonction α, qui à un instant t et à un point x associe, le point image de la solution s de (1) vérifiant l'égalité s(0) = x. Si la fonction f est de classe C^p, alors le flot α l'est aussi. Une démonstration fait usage du théorème des fonctions implicites dans le contexte d'espaces vectoriels de dimension infinie.

Ces différents exemples sont développés dans l'article détaillé.

Approche intuitive

Fonction réelle de la variable réelle

Le graphe de la fonction réciproque de f est le symétrique du graphe de f par rapport à la première bissectrice.

Le cas de la fonction réelle de la variable réelle est un peu particulier.

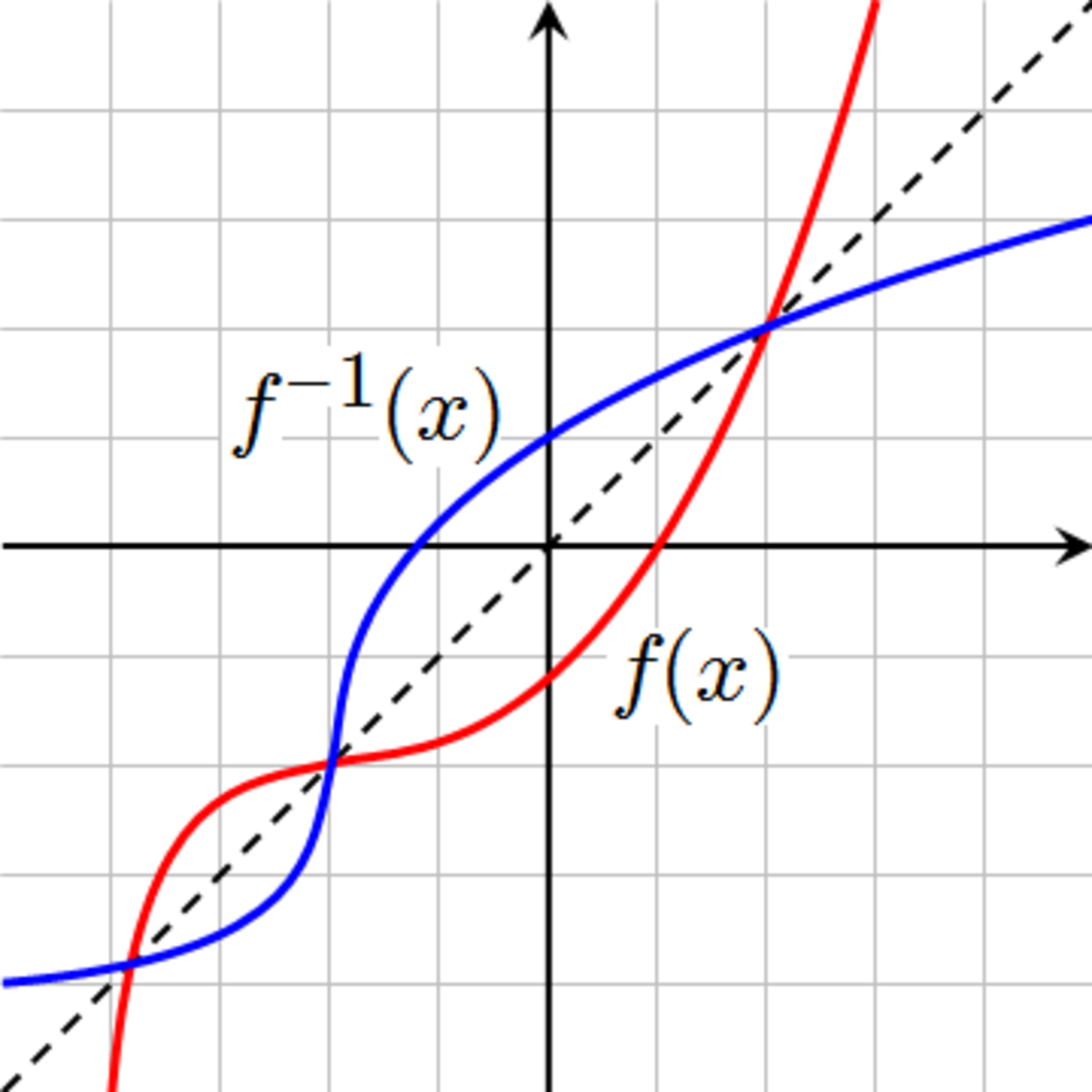
Si f est une fonction continue et strictement monotone sur un intervalle J à valeurs réelles, alors f(J) est aussi un intervalle, f est bijective de J sur f(J), et la bijection réciproque est continue (voir l'article Théorème de la bijection). Le graphe de f ^-1 est le symétrique de celui de f par rapport à la première bissectrice, d'équation x = y, comme illustré sur la figure de droite. Dans le cas particulier d'une fonction réelle de la variable réelle, les résultats sont donc plus globaux et nécessitent des hypothèses de nature différente. Ils ne sont pas généralisables, car un espace vectoriel ne dispose pas d'un ordre à l'image de l'ensemble des nombres réels.

Si de plus f est dérivable en un point a et que cette dérivée en a est non nulle alors f ^-1 est dérivable au point f(a) (voir l'article Opérations sur les dérivées). Pour cette propriété-ci, par contre, la méthode se généralise parfaitement.

Dimension deux

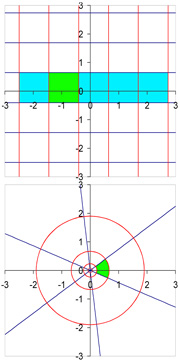
La dimension deux indique déjà l'existence d'un comportement différent du paragraphe précédent. Illustrons le pour la fonction f de R² dans R² définie par :

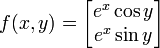
La figure de gauche indique comment le plan est transformé. L'image de la figure située en haut est illustré au dessous. Le carré vert a été déformé de manière bijective. A partir d'un point de l'image du carré vert, il est possible de reconstituer le point du carré d'origine. L'application f satisfait les hypothèses du théorème de l'article. Pour vérifier que l'application est localement inversible, il est utile de déterminer sa différentielle. Sa matrice, dite jacobienne est la suivante :

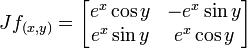
Pour savoir si la différentielle est un isomorphisme, le plus simple est de calculer son déterminant, appelé déterminant jacobien. Il est égal à exp(2x) et n'est jamais nul. L'application est en conséquence localement inversible en chaque point. A la différence des fonctions différentiables et définies sur un intervalle de R, cette propriété n'implique pas le caractère globalement injectif de f. Ajouter 2.π à la deuxième coordonnée ne modifie pas l'image par f, ainsi chaque point de R² possède une infinité d'antécédents, à l'exception de l'origine qui n'en a pas. Cette fonction peut être vue comme l'exponentielle complexe. Sa réciproque, le logarithme complexe ne peut être défini sur C tout entier et il existe plusieurs méthodes pour le définir.

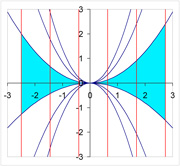
Un deuxième exemple est donné par la fonction suivante g dont le déterminant jacobien est égal à x²/2 :

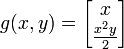
Cet exemple est illustrée avec les mêmes conventions sur la figure de droite. L'image de la zone bleu au haut à gauche est transformé en une espèce de papillon. L'application n'est pas inversible au voisinage d'un point ayant une première coordonnée nulle. Intuitivement, il est visible que les deux figures bleues ne sont pas équivalentes. Si l'on retranche le point central à celle de droite, la figure comporte alors deux composantes connexes. Le retrait d'un point quelconque sur la figure bleue à gauche ne produit jamais cet effet.