Théorème d'Abel (algèbre) - Définition

Introduction

Niels Henrik Abel présente la première démonstration rigoureuse et complète du théorème qui porte maintenant son nom.

En mathématiques, et plus précisément en algèbre, le théorème d'Abel, parfois appelé théorème d'Abel-Ruffini ou encore théorème de Ruffini, indique qu'il existe des polynômes de degré supérieur ou égal à cinq et à coefficients complexes dont les racines ne s'expriment pas par radicaux.

Ce théorème est parfois mal interprété : il n'indique pas qu'une équation de degré cinq à coefficients complexes n'admet pas de racine. Le théorème de d'Alembert-Gauss indique même l'inverse : ce type de question admet toujours au moins une solution. En revanche, cette solution ne s'exprime pas toujours par radical, ce qui signifie qu'il n'est pas toujours possible d'exprimer cette racine à partir des coefficients du polynôme, de la valeur 1, des quatre opérations auxquelles on ajoute le radical, c'est-à-dire l'extraction des racines n^ièmes.

Ce résultat est exprimé pour la première fois par Paolo Ruffini, puis démontré rigoureusement par Niels Henrik Abel. La version que l'on présente parfois est celle d'Évariste Galois qui donne une condition nécessaire et suffisante d'expression des racines sous forme de radicaux.

Préambule

Signification du théorème

Le théorème d'Abel, avec le théorème de d'Alembert-Gauss, forment les deux théorèmes fondamentaux de la théorie des équations, c'est-à-dire la théorie qui traite des équations polynomiales ou équivalentes. Une équation est dite polynomiale si elle est de la forme P(X) = 0, où P désigne un polynôme. Le théorème de d'Alembert-Gauss indique qu'une équation à coefficients dans les entiers, les rationnels, les réels ou les complexes admet au moins une racine complexe.

Des méthodes numériques comme la méthode de Newton-Raphson ou celle de Laguerre s'appliquent indépendamment du degré de l'équation. Si n, le degré du polynôme, est petit, il existe aussi des méthodes dites algébriques pour résoudre l'équation. Ainsi, si n est égal à 2, et si P s'écrit ax² + bx + c, les racines sont données par la célèbre formule , où b² − 4ac est le discriminant du polynôme ; on dit que est un radical. Des formules analogues (mais beaucoup plus compliquées) existent pour les polynômes de degré 3 ou 4, comme le montrent les méthodes de Cardan et de Ferrari.

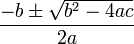
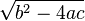
L'expression suivante d'un cosinus est aussi une expression par radical. Elle est obtenue à partir du polynôme cyclotomique correspondant aux racines dix-septièmes de l'unité (on pourrait aussi utiliser le polynôme de Tchebychev T₁₇), et permet la construction à la règle et au compas de l'heptadécagone régulier (le polygone réguler à 17 côtés) qui fut découverte par Gauss (c'est le théorème de Gauss-Wantzel) :

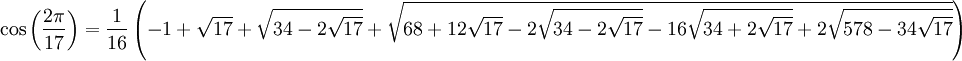
Mais malgré l'exemple précédent, pour les degrés strictement supérieurs à 4, et en dépit de plusieurs siècles d'efforts, aucune formule générale analogue à celles des degrés 2, 3 et 4 n'avait pu être trouvée. Le théorème d'Abel exprime le fait qu'aucune formule de cette nature n'existe. Une méthode pour exprimer néanmoins les racines consiste à faire usage d'une famille de fonctions plus vaste que celle des racines n^ièmes, telle que celle des fonctions elliptiques ; mais les formules ainsi obtenues n'ont qu'un intérêt théorique ; en pratique, il est bien plus intéressant d'obtenir des valeurs approchées à l'aide, par exemple, de la méthode de Newton.

Expressions du théorème

L'expression la plus proche de celle d'Abel est la suivante :

• Il n'existe pas de formule générale exprimant les solutions de l'équation du cinquième degré sous forme de radicaux.

Évariste Galois est l'auteur d'une forme plus aboutie du théorème. Sa méthode est celle généralement utilisée pour démontrer le théorème. Cette formulation prend parfois le nom de Théorème d'Abel, souvent aucun nom n'est indiqué et plus rarement le nom de théorème d'Abel-Galois. Sa formulation est plus générale car elle s'applique à un corps commutatif K quelconque et non plus uniquement au corps C des nombres complexes. Elle indique aussi si une équation algébrique est résoluble par radicaux ou non.

Soit P un polynôme à coefficients dans un corps commutatif K et L son corps de décomposition. Si l'extension L est séparable alors :

• Le polynôme P est résoluble par radicaux si et seulement son groupe de Galois est résoluble.

Le polynôme X⁵ - 3X - 1 n'est pas résoluble par radicaux, c'est-à-dire qu'il n'est pas possible d'exprimer les racines de ce polynôme sous forme de radical. Le groupe de Galois de ce polynôme est le groupe symétrique d'ordre 5, qui n'est pas résoluble (une démonstration est en donnée dans l'article groupe alterné).

Radical

Soit K un corps commutatif et L une extension de K.

• On appelle radical de K dans L un élément l de L tel qu'il existe une puissance de l élément de K. De même, on appelle radical d'une suite S d'éléments de L, un élément de l de L tel qu'il existe une puissance de l, élément de la suite S.
• On dit qu'un élément l de L s'exprime par radicaux de K si et seulement s'il existe p suites finies S_i avec i variant de 0 à p-1 telles que:

- S₀ est une suite de K

- Si i est un entier compris entre 1 et p - 1 alors S_i est une suite de combinaisons linéaires à coefficients dans K de radicaux de la suite S_i-1.

- l est une combinaison linéaire à coefficients dans K d'éléments de la suite S_p-1

• On dit qu'un polynôme est résoluble ou résoluble par radicaux si et seulement si toutes ses racines s'expriment par radicaux de K.

Formalisme de la théorie de Galois

L'expression de la version de Galois du théorème fait usage d'un vocabulaire particulier, issu de la théorie de Galois. Le corps de décomposition L de P désigne le plus petit corps contenant K ainsi que toutes les racines de P. On montre qu'un tel corps existe et est unique, à un isomorphisme près. On suppose que L est une extension séparable, c'est-à-dire qu'aucun polynôme irréductible à coefficient dans L ne possède de racine multiple. Cette propriété de séparabilité est très générale, elle est toujours vérifiée si le corps K est de caractéristique nulle, comme pour Q, R ou C ou encore n'importe quel corps de nombres.

Une structure clé pour exprimer cette version du théorème est le groupe de Galois, c'est le groupe des automorphismes de corps de L, laissant invariant K. Ce groupe est non vide puisqu'il contient au moins l'identité. On démontre que si n est la dimension de L, vu comme espace vectoriel sur K, le groupe de Galois est fini et d'ordre n (cf l'article extension de Galois).

Comprendre le théorème suppose la compréhension du terme groupe résoluble. Pour que le théorème d'Abel s'applique, il faut que le groupe de Galois G de P soit au moins un peu commutatif. Un premier cas de figure est celui ou G est commutatif au sens classique du terme, le groupe est résoluble. Il peut aussi exister un sous-groupe normal G₁ de G commutatif et un groupe H abélien tel que le produit semi-direct de G₁ par H soit isomorphe à G. Dans ce cas, le théorème d'Abel s'applique encore et H est isomorphe au groupe quotient G/G₁. Dans le cas général :

• Un groupe G est dit résoluble lorsqu'il existe une suite finie G₀, G₁,...,G_n de n+1 sous-groupes de G telle que :

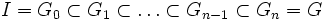
où G_k, pour tout k compris entre 0 et n; est un sous-groupe distingué de G_k+1 et le groupe quotient G_k+1/G_k est abélien. Le groupe I désigne le sous-groupe constitué uniquement de l'élément neutre de G.