Théorème d'Abel (algèbre) - Définition

Exemples

Le cas du second degré

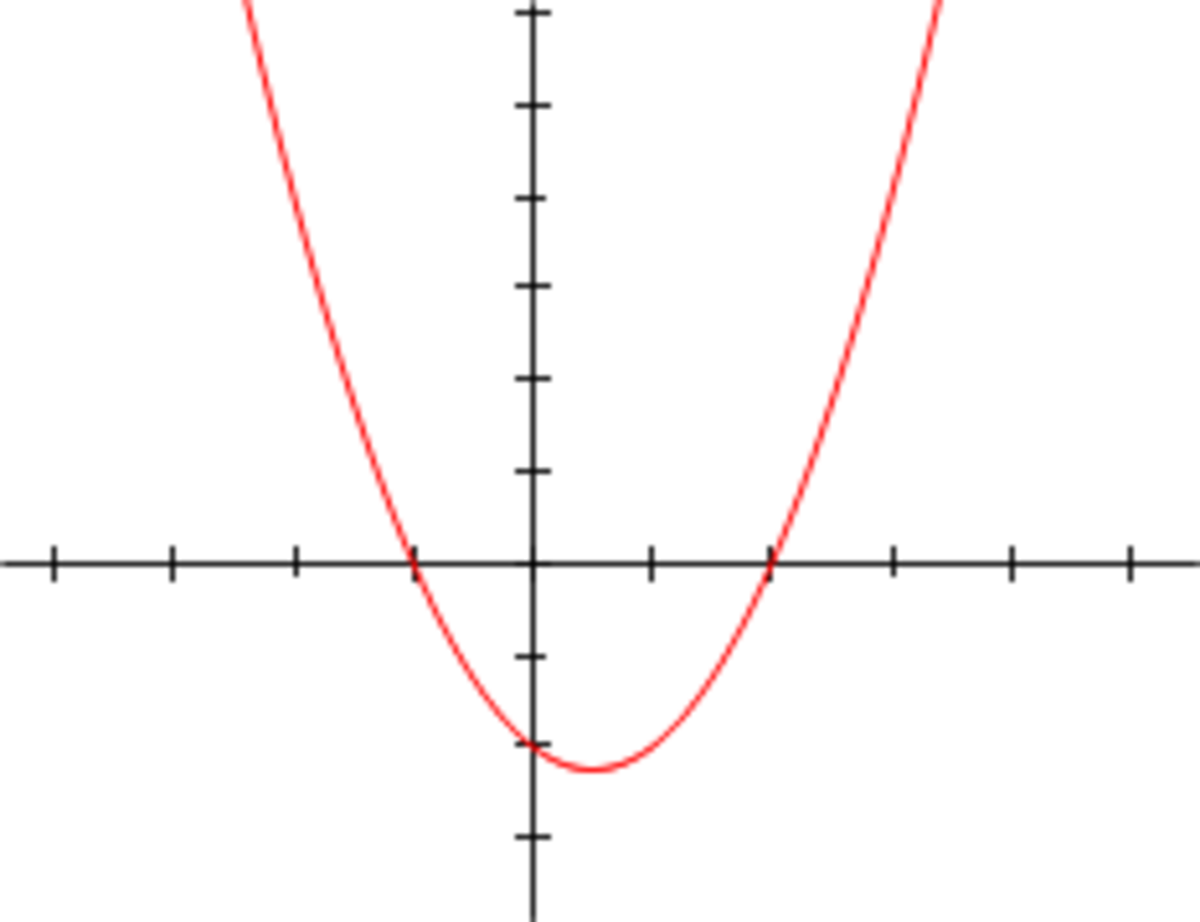
Considérons le cas où le polynôme P[X] est de degré deux à coefficients rationnels n'ayant pas de racine rationnelle. Quitte à diviser l'équation, il est possible de considérer que :

Notons x₁ et x₂ les deux racines de l'équation. On en déduit :

L'extension est de degré deux et L est un espace vectoriel sur les rationnels de dimension deux. Comme l'extension est galoisienne le groupe de Galois G est d'ordre deux, il existe donc un morphisme m du groupe de Galois différent de l'identité tel que m² soit égal à Id l'identité de L. Le polynôme minimal de m est donc un diviseur de X²-1. Les valeurs propres de m sont donc 1 car l'ensemble des rationnels est invariant par m et -1 car m est différent de l'identité. Considérons alors une base de L (1,r) telle que r soit une valeur propre de m et telle que x₁ = a + r. Alors x₂ s'exprime aussi dans la base, il existe donc deux rationnels a' et b' tels que x₂ = a' + b'r.

Or la somme des racines est rationnelle donc b' est égal à -1. De plus, le produit des racines est aussi rationnel donc a' est égal à a. On en déduit :

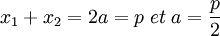
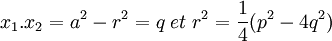
Le groupe de Galois permet donc une résolution effective de l'équation quadratique.

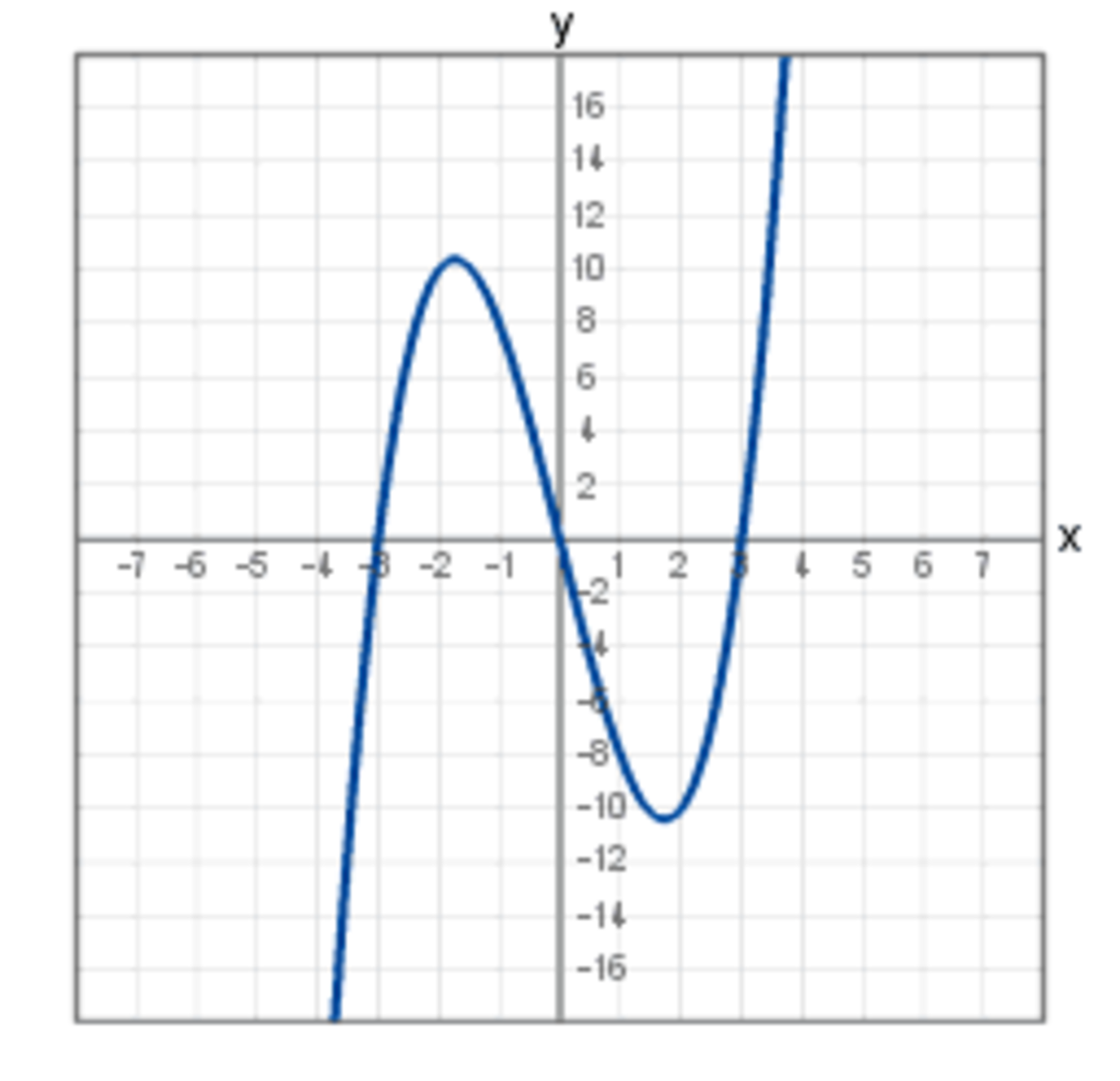
Le cas du degré trois

La méthode de Cardan permet d'extraire la ou les racines d'un polynôme de degré 3 dans le cas général.

Généralités

Considérons le cas où le polynôme P[X] est de degré trois à coefficients rationnels et irréductible. Quitte à diviser l'équation et à translater la variable, il est possible de considérer que:

Notons x₁, x₂ et x₃ les trois racines de l'équation. On en déduit:

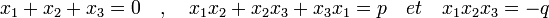
Le corps de décomposition L contient la racine x₁ dont le polynôme minimal est de degré trois, donc L est au moins de dimension trois sur le corps des rationnels. Le groupe de Galois de P[X] est donc isomorphe à un sous-groupe d'ordre au moins trois du groupe symétrique S₃ qui, lui, est d'ordre six. Le groupe de Galois est donc isomorphe soit à S₃, soit à son sous-groupe d'ordre trois, le groupe alterné A₃.

A₃ est un groupe résoluble car il est abélien (et même cyclique). S₃ contient un sous-groupe distingué abélien A₃, et le quotient S₃/A₃ (groupe cyclique d'ordre deux) est abélien. En conséquence S₃ est aussi résoluble. Dans tous les cas, le groupe de Galois est résoluble, donc le théorème d'Abel-Ruffini garantit que le polynôme l'est aussi.

Détermination du groupe de Galois

Le groupe de Galois est égal à S₃ si et seulement s'il contient un élément dont la signature (le groupe de Galois est ici identifié au groupe des permutations des racines) est égal à -1. Soit g un élément du groupe ; on a alors l'égalité:

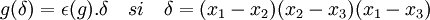
où ε(g) désigne la signature de g. On en déduit que le groupe de Galois contient un élément de signature impaire si et seulement si δ a pour image par un élément du groupe − δ. Dans le cas contraire δ est invariant par tous les éléments du groupe, ce qui est une condition nécessaire est suffisante pour que δ soit un rationnel (cf la quatrième propriété du paragraphe sur le théorème fondamental de la théorie de Galois). On remarque de plus que le carré de ce nombre est toujours un rationnel. On vérifie alors que:

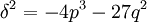
On en déduit la condition nécessaire et suffisante:

• Le groupe de Galois de P[X] est égal à A₃ si et seulement si - 4p³ - 27q² est le carré d'un rationnel.

Calcul des racines

Dans l'extension Q[δ], le groupe de Galois ne contient que des éléments d'ordre trois. Pour plus de commodité, considérons alors l'extension L₁ comme égale à Q[δ, j] où j désigne la première racine cubique de l'unité (celle de partie imaginaire strictement positive). Les deux éléments δ et j sont des éléments d'ordre deux, L₁ ne peut donc contenir les racines du polynôme. Soit m le morphisme du groupe de Galois défini par:

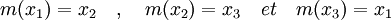
Le morphisme m est défini par une permutation de signature paire, et le groupe de Galois contient les trois permutations de signature paire, m est donc bien un élément du groupe.

Le polynôme caractéristique de m considéré comme un endomorphisme de l'espace vectoriel L sur L₁ est égal à X³-1 = 0. Il admet trois racines 1, j et j² qui sont donc trois valeurs propres. Il existe donc une base de vecteurs propres et x₁ = u + v + w où m(u)=ju, m(v)=j²v et m(w)=w. Il ne reste alors plus qu'à calculer u, v et w en fonction des coefficients du polynôme.

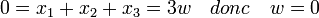
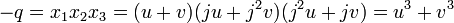
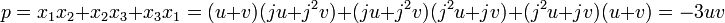
Le système d'équations suivant permet alors de conclure :

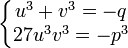
Un exemple de degré seize

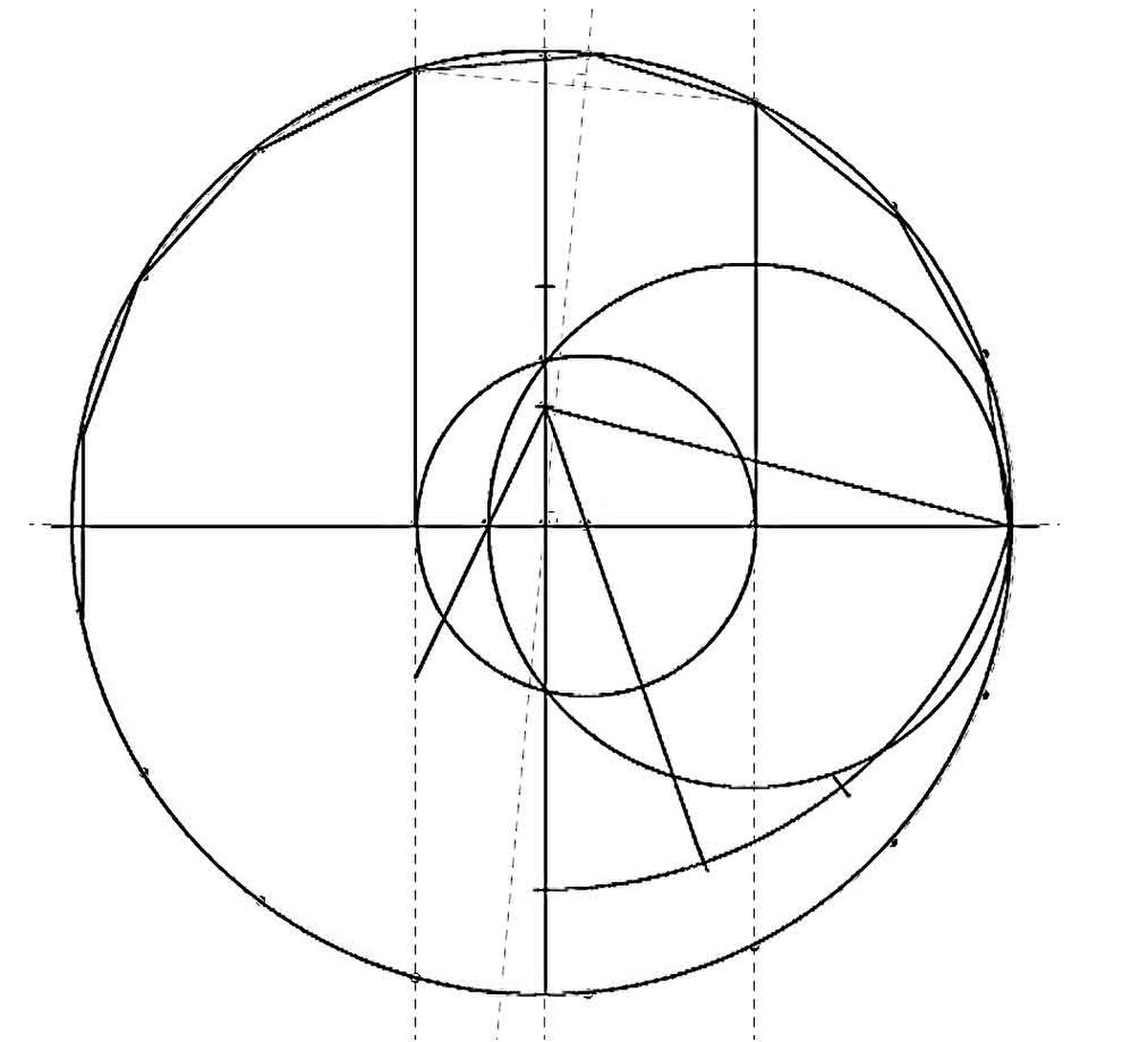
Certains polynômes, malgré leurs degrés élevés, sont résolubles par radicaux. Carl Friedrich Gauss a étudié les polynômes cyclotomiques en 1801 pour, entre autres choses, construire à la règle et au compas l'heptadécagone, c’est-à-dire le polygone régulier à 17 côtés. Il a considéré le polynôme suivant:

C'est le polynôme cyclotomique correspondant au troisième nombre premier de Fermat. Montrons que son groupe de Galois est isomorphe au groupe cyclique d'ordre seize.

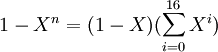
L'égalité précédente montre que les seize racines d'ordre dix-sept différentes de l'unité sont des racines du polynôme. Soit z la première racine primitive: exp(i.2.pi/17) et m un morphisme de l'extension du corps des nombres rationnels contenant les seize racines différentes de un. Alors m(z) est aussi une racine, il existe donc un entier p tel que m(z)= z^p. On en déduit que si n est un entier alors : m(zⁿ)= z^n.p. Réciproquement si p est un entier compris entre un et seize alors l'application qui à zⁿ associe z^n.p définit bien un élément du groupe de Galois. Le groupe de Galois est donc un groupe à seize éléments isomorphe au groupe cyclique d'ordre seize.

La fin des calculs se trouve dans le paragraphe Cas de l'heptadécagone.

Un contre-exemple de degré cinq

L'article détaillé montre que l'équation X⁵ - 3X - 1 = 0 ne possède pas de racine s'exprimant par radicaux dans l'ensemble Q des nombres rationnels.