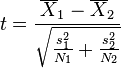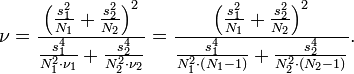Test t de Welch - Définition

Introduction

En statistiques, le test t de Welch est une adaptation du test t de Student. Il peut être utilisé notamment pour tester statistiquement l’hypothèse d’égalité de deux variances. Il s'agit en fait d'une solution approchée du problème de Behrens-Fisher.

Formules

Le test t de Welch définit le t statistique par la formule suivante :

où , s² et N correspondent respectivement à la moyenne d'un échantillon, à sa variance et à la taille de l'échantillon. Contrairement au test t de Student, le dénominateur n'est pas basé sur une estimation de l'ensemble des variances.

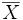
Le calcul des degrés de liberté ν associés à cette estimation de la variance est approché par l'équation de Welch-Satterthwaite :

Ainsi ν_i = N_i − 1, les degrés de liberté sont associés à la nième estimation de la variance.

Test statistique

Une fois le t et ν calculés, ces statistiques peuvent être utilisés avec une distribution t pour tester l'hypothèse nulle qui stipule que les moyennes de deux populations sont égales (utilisant un test bilatéral), ou l'hypothèse nulle stipulant que la moyenne d'une population est plus grande ou égale à une autre (utilisant un test unilatéral). Lorsque le test est réalisé, celui-ci donne une p-value qui permettra de rejeter ou non l'hypothèse nulle.