Test de Kolmogorov-Smirnov - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En statistiques, le test de Kolmogorov-Smirnov est un test d'hypothèse utilisé pour déterminer si un échantillon suit bien une loi donnée connue par sa fonction de répartition continue, ou bien si deux échantillons suivent la même loi.
Principe
Ce test repose sur les propriétés des Fonction de répartition empirique : si
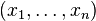
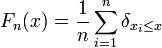
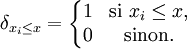
La fonction de répartition empirique est un processus qui prend ses valeurs dans l'espace des fonctions croissantes comprises entre 0 et 1. Grâce à ses propriétés, on a la convergence suivante :
![\mathbb{P}\left[ \sup_{x} |F_n(x)-F(x)|>\frac{c}{\sqrt{n}} \right]\xrightarrow[n\to\infty]{} \alpha(c)= 2\sum_{r=1}^{+\infty} (-1)^{r-1}\exp(-2r^2c^2)](https://upload.wikimedia.org/math/5/a/7/5a74d0e11f682b634470811491af9b75.png)
pour toute constante c > 0. Le terme α(c) vaut 0.05 pour c = 1.36. Remarquons que la limite à droite ne dépend pas de F. Cela découle du fait que
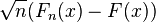
Il est ainsi facile de proposer un test d'hypothèse pour décider si un échantillon provient bien d'une loi donnée, ou si deux échantillons ont la même loi, lorsque leurs fonction de répartitions sont continues.
On peut aussi considérer maxx(Fn(x) − F(x)) et maxx(F(x) − Fn(x)).
Le test de Kolmogorov-Smirnov est par exemple utilisé pour tester la qualité d'un générateur de nombres aléatoires.
Exemple
On illustre le test en simulant trois variables aléatoires: x et y de loi normale, z de loi uniforme. On applique ensuite le test de même distribution sur les trois paires puis le test d'adéquation à une distribution connue, en utilisant la fonction ks.test() du logiciel libre de statistiques R.
Génération de variables aléatoires x, y et z
x <- rnorm(50) #Simulation de 50 observations d'une loi normale y <- rnorm(40) #Simulation de 40 observations d'une loi normale z <- runif(30) #Simulation de 30 observations d'une loi uniforme
Test d'adéquation de distribution de deux échantillons
Test de x et y
| Résultat affiché | Code R |
|---|---|
| Two-sample Kolmogorov-Smirnov test data: x and y D = 0.135, p-value = 0.7652 alternative hypothesis: two-sided | ks.test(x, y) |
Si l'hypothèse nulle est vraie (c'est-à-dire que les deux échantillons proviennent d'une même loi), alors la probabilité d'observer une statistique D autant éloignée de 0 (qui correspondrait à une parfaite adéquation des deux échantillons) ou plus éloignée, vaut 0.7 (les chiffres obtenus en reproduisant l'exemple peuvent varier!).
Test de x et z
| Résultat affiché | Code R |
|---|---|
| Two-sample Kolmogorov-Smirnov test data: x and z D = 0.48, p-value = 0.0002033 alternative hypothesis: two-sided | ks.test(x, z) |
Si l'hypothèse nulle est vraie (c'est-à-dire que les deux échantillons x et z proviennent d'une même loi), alors la probabilité d'observer une statistique D autant éloignée de 0 (qui correspondrait à une parfaite adéquation des deux échantillons) ou plus éloignée, est extrêmement petite et vaut moins de 0.1%. Il s'agit donc d'un cas très improbable (il est très rare que D soit si grand si l'hypothèse nulle est vraie) qui nous incite à rejeter l'hypothèse de même distribution.
Test de y et z
| Résultat affiché | Code R |
|---|---|
| Two-sample Kolmogorov-Smirnov test data: y and z D = 0.55, p-value = 2.889e-05 alternative hypothesis: two-sided | ks.test(y, z) |
Si l'hypothèse nulle est vraie (c'est-à-dire que les deux échantillons y et z proviennent d'une même loi), alors la probabilité d'observer une statistique D autant éloignée de 0 (qui correspondrait à une parfaite adéquation des deux échantillons) ou plus éloignée, est extrêmement petite et vaut moins de 0.1%. Il s'agit donc d'un cas très improbable (il est très rare que D soit si grand si l'hypothèse nulle est vraie) qui nous incite à rejeter l'hypothèse de même distribution.
Test d'adéquation d'un échantillon à une distribution connue
Test si x suit une loi normale
| Résultat affiché | Code R |
|---|---|
| One-sample Kolmogorov-Smirnov test data: x D = 0.0824, p-value = 0.8586 alternative hypothesis: two-sided | ks.test(x, "pnorm") |
La probabilité est ici de 80%, on ne rejette donc pas l'hypothèse (qui est vraie puisque x est généré selon une loi normale) que x suit une loi normale.
Test si x suit une loi uniforme
| Résultat affiché | Code R |
|---|---|
| One-sample Kolmogorov-Smirnov test data: x D = 0.5501, p-value = 1.033e-14 alternative hypothesis: two-sided | ks.test(x, "punif") |
La probabilité est ici de moins de 0.01%, on rejette donc l'hypothèse (qui est fausse puisque x est généré selon une loi normale) que x suit une loi uniforme.
