Tenseur - Définition

Typologie

Dans le cas de l'ordre 2, un tenseur peut être symétrique ou antisymétrique (ou ni l'un, ni l'autre).

Pour un tenseur symétrique, on a la relation T_ab = T_ba.

Pour un tenseur antisymétrique, on a la relation T_ab = -T_ba.

En général, un tenseur n'est ni symétrique, ni antisymétrique. Un tenseur quelconque peut cependant être décomposé en une partie symétrique S et une partie antisymétrique A, avec les relations :

• S_ab = 1/2(T_ab + T_ba )
• A_ab = 1/2(T_ab - T_ba )

Les parties symétriques et antisymétriques réunies rassemblent autant d'information que le tenseur originel.

Cette règle peut être étendue aux tenseurs d'ordre quelconque. On dira alors que le tenseur est symétrique pour une paire d'indice, s'il est invariant par échange des deux indices, et qu'il est antisymétrique pour une paire d'indice s'il se transforme en son opposé par échange des deux indices.

Les indices de la paire considérée doivent avoir même valence.(Dans le cas contraire la propriété de symétrie dépendrait de la base choisie).

Dans le cas particulier d'un espace vectoriel de dimension 3, un tenseur antisymétrique d'ordre 2 porte le nom de pseudovecteur. (dont la matrice n'est antisymétrique qu'en base orthonormale ou si...)

Tenseur symétrique

Un tenseur est symétrique s'il est inchangé par des permutations des indices hauts ou une permutation des indices bas. Un tenseur d'ordre (0,2) ou bien (2,0) est symétrique si et seulement si ses composantes forment une matrice symétrique. Le fait pour une matrice d'être symétrique ne dépend pas de la base choisie (la propriété est conservée entre deux matrices semblables).

Tenseurs antisymétriques

Un tenseur est antisymétrique si, par une permutation quelconque des indices, il subit un changement de signe qui est le signe de la permutation. Un tenseur d'ordres (0,2) ou (2,0) est antisymétrique si et seulement si ses composantes forment une matrice antisymétrique. Pour un tenseur antisymétrique, les composantes dans lesquelles un indice se répète au moins deux fois sont toutes nulles. Par exemple, les j composantes T_iij du tenseur T_abc sont nulles. De ce fait, un tenseur de type (h,k) avec k > n ou h > n est nécessairement nul, parce que l'on ne peut avoir k (ou h) valeurs différentes dans . En outre (à une multiplication par un scalaire près), il existe un seul tenseur antisymétrique d'ordre (0,n) : le déterminant, ou tenseur de Levi-Civita.

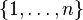
Les tenseurs antisymétriques sont utilisés pour construire les formes differentielles.