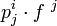Tenseur - Définition

Composantes

Vecteurs

Dans la base , les composantes du vecteur sont (u₁, u₂, u₃). Dans la base , elles sont (u'₁, u'₂, u'₃). On cherche comment passer de l'une à l'autre des représentations.

Dans la base B, les vecteurs de la base B' s'écrivent :

Par définition d'une base, chaque vecteur se décompose selon une combinaison linéaire unique des vecteurs de B'. On peut ainsi définir la matrice de changement de base P de B vers B' :

les colonnes de la matrice de changement de base sont les coordonnées des vecteurs de l'ancienne base dans la nouvelle. On a alors

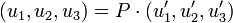et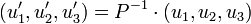

.

Lorsque les deux bases B et B' sont orthonormées, P vérifie en outre

P ^{− 1} = ^tP.

Le changement de base se fait par multiplication d'une seule matrice de changement de base, le tenseur est dit d'ordre 1.

Matrices

Une matrice M représente une application linéaire ƒ d'un espace vers un autre pour une base donnée dans chaque espace. On peut donc changer de base dans l'espace de départ et dans l'espace d'arrivée. On peut donc définir deux matrices, P₁ et P₂ pour chacun des espaces. La matrice M' représentant ƒ pour les deux nouvelles bases se calcule donc en faisant

Le changement de base se fait par multiplication de deux matrices de changement de base, le tenseur est dit d'ordre 2.

Formes linéaires

Considérons un espace à trois dimensions muni d'une base non orthogonale (on va la supposer normée pour simplifier la présentation). En effet, il y a de nombreux exemples dans la nature où il y a des axes « naturels » qui ne sont pas orthogonaux, par exemples les axes de certains cristaux. En fait, lorsqu'un phénomène est anisotrope, on peut souvent trouver des axes dits « principaux » pour lesquels les calculs se simplifient, et ces axes ne sont pas toujours orthogonaux.

Considérons une forme linéaire ƒ sur cet espace, qui à un vecteur associe un scalaire

(les indices relatifs à la forme linéaire sont notés en haut pour permettre de les distinguer). Considérons la base , dite « base duale », définie par

on a alors

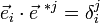(symbole de Kronecker)

soit

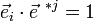si i = j

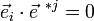sinon

Si l'on définit le vecteur

on peut alors écrire

La base des fonctions g ⁱ « produit scalaire par  »

est une base des formes linéaires de l'espace ; on identifie souvent cette base de fonctions (g ⁱ ) avec la base de vecteurs elle-même. L'espace vectoriel formé par les formes linéaires est appelé « espace dual » ou « espace réciproque ».

Si l'on fait un changement de base de l'espace direct, alors les composantes du vecteur se transforment selon

où p ^j_i est le coefficient de la matrice de changement de base (noté e_ji dans le paragraphe précédent). En revanche, les composantes de se transforment selon

on voit que dans le cas du changement de la base de formes linéaires, on multiplie par la matrice de changement de base, alors que dans le cas du changement de la base de vecteurs, on multiplie par sa transposée.

Variance

On voit donc que l'on a deux types d'indices. D'une part des indices de type « vecteur », notés avec un indice en bas (par exemple u_i ), obtenus par projection du vecteur sur les axes parallèlement aux autres axes, et se transformant lors d'un changement de base par le produit de la transposée de la matrice de changement de base (P). Ces indices sont dits contravariants.

D'autre part des indices de type « forme linéaire », notés avec un indice en haut (par exemple ƒⁱ ), obtenus par projection sur les axes perpendiculairement aux axes ( et sont perpendiculaires à ), et se transformant lors d'un changement de base par le produit de la matrice « directe » de changement de base (P). Ces indices sont dites covariants.

D'après la formule de changement de base des matrices, on voit que celles-ci sont une fois covariantes, une fois contravariantes, on devrait donc noter M_i ^j. Toutefois, on n'utilise que rarement cette notation tensorielle pour les matrices.

Convention d'Einstein

Un tenseur peut avoir des composantes covariantes et contravariantes, ce qui explique que certains indices soient notés en haut et d'autres en bas, par exemple T_a^bc.

On adopte souvent la convention de notation d'Einstein qui consiste à sommer lorsqu'un indice se trouve en haut et en bas dans un produit, par exemple

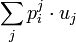et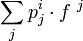

se notent respectivement

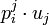et