Tenseur - Définition

Définition

Un tenseur est une application multilinéaire. L'algèbre des tenseurs est appelée algèbre tensorielle ou algèbre multilinéaire

La définition des tenseurs exposée ici est la plus intrinsèque, parce qu'elle ne fait pas usage des bases, et est la plus utilisée en mathématiques. Une définition alternative, amplement utilisée en Physique, nécessite de fixer une base et définit un tenseur par le comportement de ses composantes en cas de changement de base.

Soit V un espace vectoriel de dimension n sur un corps K. L'espace dual V ^* est l'espace vectoriel formé de toutes les formes linéaires

L'espace V ^* est aussi de dimension n. Les éléments de V et V ^* sont appelés respectivement vecteurs et covecteurs.

Un tenseur T associe alors à k vecteurs et h covecteurs un scalaire

La multilinéarité garantit que la fonction soit linéaire sur chaque variable.

L'ordre ou type du tenseur est le couple (h,k). On donne aussi le nom d'ordre ou de rang à la somme h+k.

Tenseur peut évoquer un champ de tenseurs au lieu d'un tenseur proprement dit, particulièrement en physique. Les champs de tenseurs sont des applications qui a tout point d'un espace, font correspondre un tenseur particulier. On peut de ce fait considérer un champ de tenseurs comme tenseur dépendant d'un point de l'espace. Les opérations usuelles sur les tenseurs sont alors étendues aux champs de tenseurs.

Représentation

Dans le cas où l'espace vectoriel V est de dimension finie n, on se donne une base de V. On peut alors représenter le tenseur T par une grandeur indicée h + k fois où chacun des indices va de 1 à n : .

On appelle composante chacun des nombres T_i,j,k,...
Chaque indice multiplie le nombre de composantes nécessaires par n.
Représenter un tenseur d'ordre donné nécessite donc n^ordre composantes.

Pour distinguer les indices qui correspondent à ceux d'un vecteur ou d'un covecteur dans la définition, on mettra ces indices en haut pour les contravariants, en bas pour les covariants. voire le titre Composantes. Par exemple, avec h=1 et k=2 on aura 1 indice haut et deux indices bas. On notera le tenseur par , et chacune des n³ composantes par un nombre .

Ordres 0, 1 et 2

• Lorsque l'on dispose d'une base d'un espace vectoriel E sur un corps , tout vecteur de cet espace peut se décrire par ses coordonnées dans cette base. Ainsi, dans une base 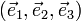donnée,
  le vecteur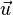 sera décrit par ses composantes
  (u₁, u₂, u₃).
  Si l'on change de base, les composantes (les nombres u₁, u₂ et u₃) changent, mais le vecteur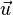 reste le même. Le tenseur représente l'ensemble des représentations de 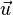dans toutes les bases. Un vecteur est un tenseur dit « d'ordre 1 ».

• De même, une application linéaire ƒ d'un espace E vers un espace F est décrite par une matrice M dont les coefficients dépendent de la base de E et de celle de F. Le tenseur représente l'ensemble des représentations de ƒ dans toutes les bases. Une matrice est un tenseur dit « d'ordre 2 ».

• Un scalaire est un simple nombre, qui ne dépend d'aucune base. On dit que le scalaire est un « tenseur d'ordre 0 ».

Ordre n

Une autre manière de voir est la suivante : une matrice M peut se noter par ses coefficients (M_ij), ou plutôt , voir plus loin — soit deux indices —, un vecteur par ses composantes (u_i) — soit un indice —, et un scalaire a simplement par lui-même — soit zéro indice.

On peut envisager des objets définis avec trois, quatre, n indices .

Un objet défini par n indices et vérifiant les formules de changement de base est un tenseur d'ordre n (cf. distinction entre vecteurs et pseudovecteurs).

Sur un espace vectoriel de dimension finie m, chaque indice peut prendre les valeurs de 1 à m. Un tenseur d'ordre n sur cet espace vectoriel a donc mⁿ coefficients. Si le tenseur « relie » n espaces vectoriels de dimensions différentes m₁,m₂,...m_n, alors le tenseur contient coefficients.

Un tel tenseur d'ordre n représente une application multi-linéaire (forme n-linéaire) de E×E×… ×E dans  :

On retrouve les coefficients du tenseur T en identifiant .

Notations

Dans les notations, T_ijk... représente la composante du tenseur T de coordonnées (i,j,k,...). Quand on veut désigner un tenseur dans sa globalité tout en indiquant l'ordre de ce tenseur, on peut souligner le nom du tenseur d'autant de trait que l'ordre du tenseur. Ainsi, avec cette notation, un vecteur sera noté plutôt que , et un tenseur de contraintes mécaniques (d'ordre 2) sera noté . Ceci est particulièrement utile quand on manipule des tenseurs d'ordres différents, ce qui est le cas en déformation élastique, pour laquelle on caractérise le comportement de déformation des matériaux par un tenseur d'ordre 4, et les déformations et contraintes par des tenseurs d'ordre 2. Dans le cas le plus simple de comportement élastique linéaire, .