Vendredi 25 Avril 2025
Rechercher 🔍

Tenseur métrique - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Définition - Coordonnées rectilignes - Pseudo-métrique - Montée et descente d'indices - Cas des coordonnées curvilignes - Changement de base - Distances et angles - Quelques exemples - Produit avec sa dérivée partielle

Changement de base

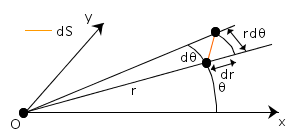
Lors d'un changement de base, le tenseur métrique se transforme de la manière suivante ( M est la matrice de passage d'une base dont on connait la métrique g vers une autre base ):

g'_{kl} = M^i_{\ k} M^j_{\ l}\ g_{ij}

ou en notation matricielle:

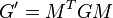
G' = M^TGM~

Distances et angles

La longueur d'un segment d'une courbe paramétrée par t partant du point a et arrivant au point b est définie par :

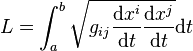
L = \int_a^b \sqrt{ g_{ij} \frac{\mathrm dx^i}{\mathrm dt} \frac{\mathrm dx^j}{\mathrm dt}}\mathrm dt

où (x1(t),...,xn(t)) est l'équation décrivant cette courbe dans le système de coordonnées local.

On l'écrit souvent avec la notation :

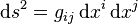
\mathrm ds^2 = g_{ij}\,\mathrm dx^i\,\mathrm dx^j .

L'angle θ entre deux vecteurs tangents u et v est défini par :

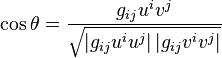
\cos \theta = \frac{g_{ij}u^iv^j} {\sqrt{ \left| g_{ij}u^iu^j \right| \left| g_{ij}v^iv^j \right|}}

Note: En coordonnées rectilignes, les vecteurs ne sont pas nécessairement tangents.

Quelques exemples

Exemple 1

Dans un espace euclidien à 2 dimensions, et en prenant un repère cartésien orthonormé, le tenseur métrique est :

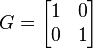
G = \begin{bmatrix} 1 & 0 \\ 0 & 1\end{bmatrix}

et la longueur d'une courbe vaut :

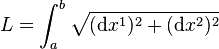
L = \int_a^b \sqrt{ (\mathrm dx^1)^2 + (\mathrm dx^2)^2}

Exemple 2

On se propose de calculer le tenseur métrique pour un espace euclidien et le système de coordonnées sphériques. Les équations suivantes nous donnent les coordonnées (x,y,z) exprimées dans un repère orthonormé cartésien en fonction des coordonnées sphériques (r,θ,φ) (voir ci-dessous).

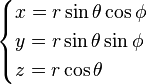
\begin{cases} x=r\sin\theta \cos\phi \\ y=r\sin\theta \sin\phi \\ z=r\cos\theta \end{cases}

On peut maintenant écrire la matrice jacobienne :

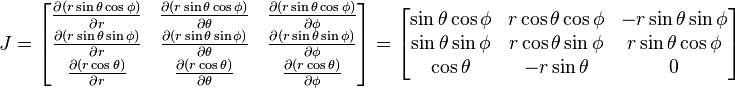
\quad J = \begin{bmatrix} \frac{\partial (r\sin\theta \cos\phi)}{\partial r} & \frac{\partial (r\sin\theta \cos\phi)}{\partial \theta} & \frac{\partial (r\sin\theta \cos\phi)}{\partial \phi} \\ \frac{\partial (r\sin\theta \sin\phi)}{\partial r} & \frac{\partial (r\sin\theta \sin\phi)}{\partial \theta} & \frac{\partial (r\sin\theta \sin\phi)}{\partial \phi} \\ \frac{\partial (r\cos\theta)}{\partial r} & \frac{\partial (r\cos\theta)}{\partial \theta} & \frac{\partial (r\cos\theta)}{\partial \phi} \end{bmatrix} = \begin{bmatrix} \sin\theta \cos\phi & r\cos\theta \cos\phi & -r\sin\theta \sin\phi \\ \sin\theta \sin\phi & r\cos\theta \sin\phi & r\sin\theta \cos\phi \\ \cos\theta & -r\sin\theta & 0 \end{bmatrix}

Le tenseur métrique est le produit de la matrice jacobienne transposée et de la jacobienne :

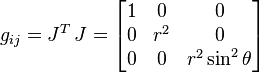
g_{ij} = J^T\,J = \begin{bmatrix} 1 & 0 & 0 \\ 0 & r^2 & 0 \\ 0 & 0 & r^2\sin^2\theta \end{bmatrix}
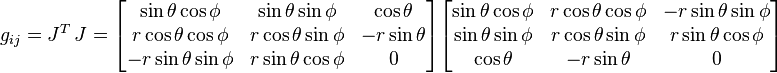
g_{ij} = J^T\,J = \begin{bmatrix} \sin\theta \cos\phi & \sin\theta \sin\phi & \cos\theta \\ r\cos\theta \cos\phi & r\cos\theta \sin\phi & -r\sin\theta \\ -r\sin\theta \sin\phi & r\sin\theta \cos\phi & 0 \end{bmatrix} \begin{bmatrix} \sin\theta \cos\phi & r\cos\theta \cos\phi & -r\sin\theta \sin\phi \\ \sin\theta \sin\phi & r\cos\theta \sin\phi & r\sin\theta \cos\phi \\ \cos\theta & -r\sin\theta & 0 \end{bmatrix}
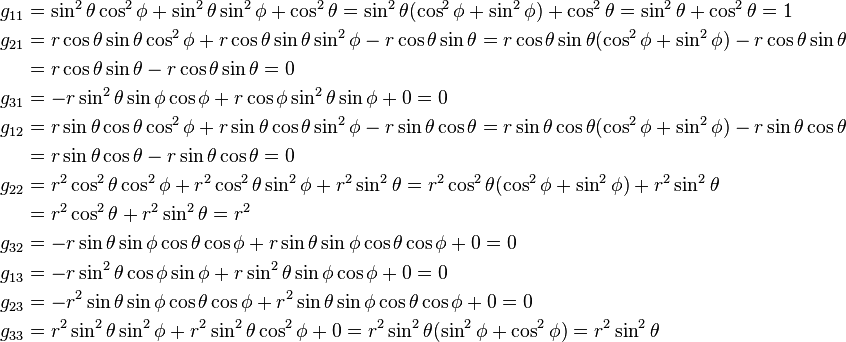
\begin{align} g_{11} &= \sin^2\theta \cos^2\phi + \sin^2\theta \sin^2\phi + \cos^2\theta = \sin^2\theta ( \cos^2\phi + \sin^2\phi ) + \cos^2\theta = \sin^2\theta + \cos^2\theta = 1 \\ g_{21}&= r\cos\theta \sin\theta \cos^2\phi + r\cos\theta \sin\theta \sin^2\phi - r\cos\theta \sin\theta = r\cos\theta \sin\theta (\cos^2\phi + \sin^2\phi) - r\cos\theta \sin\theta \\ &= r\cos\theta \sin\theta - r\cos\theta \sin\theta = 0 \\ g_{31}&= -r\sin^2\theta \sin\phi \cos\phi + r\cos\phi \sin^2\theta \sin\phi + 0 = 0 \\ g_{12} &= r\sin\theta \cos\theta \cos^2\phi + r\sin\theta \cos\theta \sin^2\phi -r \sin\theta \cos\theta = r\sin\theta \cos\theta ( \cos^2\phi + \sin^2\phi ) -r \sin\theta \cos\theta \\ &= r\sin\theta \cos\theta -r\sin\theta \cos\theta = 0 \\ g_{22}&= r^2\cos^2\theta \cos^2\phi + r^2\cos^2\theta \sin^2\phi + r^2\sin^2\theta = r^2\cos^2\theta ( \cos^2\phi + \sin^2\phi ) + r^2\sin^2\theta \\ &= r^2\cos^2\theta + r^2\sin^2\theta = r^2 \\ g_{32}&= -r\sin\theta \sin\phi \cos\theta \cos\phi +r\sin\theta \sin\phi \cos\theta \cos\phi + 0 = 0 \\ g_{13} &= -r\sin^2\theta \cos\phi \sin\phi + r\sin^2\theta \sin\phi \cos\phi + 0 = 0 \\ g_{23} &= -r^2\sin\theta \sin\phi \cos\theta \cos\phi + r^2\sin\theta \sin\phi \cos\theta \cos\phi + 0 = 0 \\ g_{33} &= r^2\sin^2\theta \sin^2\phi + r^2\sin^2\theta \cos^2\phi + 0 = r^2\sin^2\theta ( \sin^2\phi + \cos^2\phi ) = r^2\sin^2\theta \end{align}

Exemples de métriques

Coordonnées polaires

Plan euclidien, coordonnées polaires : (x1,x2) = (r,θ)

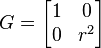
G = \begin{bmatrix} 1 & 0 \\ 0 & r^2\end{bmatrix}
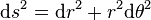
\mathrm ds^2 = \mathrm dr^2 + r^2\mathrm d\theta^2~

Espace euclidien, coordonnées cylindriques : (x1,x2,x3) = (r,θ,z)

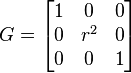
G = \begin{bmatrix} 1 & 0 & 0\\ 0 & r^2 & 0 \\ 0 & 0 & 1\end{bmatrix}
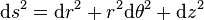
\mathrm ds^2 = \mathrm dr^2 + r^2\mathrm d\theta^2 + \mathrm dz^2~
Coordonnées sphériques

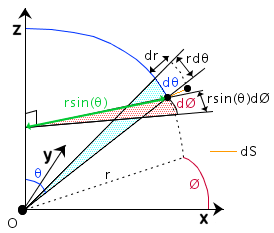
Espace euclidien, coordonnées sphériques : (x1,x2,x3) = (r,θ,φ)

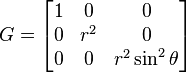
G = \begin{bmatrix} 1 & 0 & 0\\ 0 & r^2 & 0 \\ 0 & 0 & r^2\sin^2 \theta\end{bmatrix}

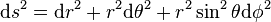
\mathrm ds^2 = \mathrm dr^2 + r^2\mathrm d\theta^2 + r^2\sin^2\theta \mathrm d\phi^2~

Espace de Minkowski, espace-temps plat (relativité restreinte) : (x0,x1,x2,x3) = (ct,x,y,z)

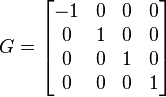
G = \begin{bmatrix} -1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{bmatrix}
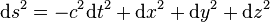
\mathrm ds^2 = -c^2\mathrm dt^2 + \mathrm dx^2 + \mathrm dy^2 + \mathrm dz^2~

Métrique de Schwarzschild (solution particulière de la relativité générale, l'espace est ici courbé) : (x0,x1,x2,x3) = (ct,r,θ,φ)

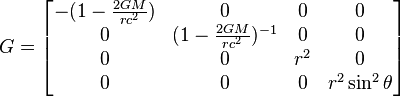
G = \begin{bmatrix} -(1-\frac{2GM}{rc^2}) & 0 & 0 & 0\\ 0 & (1-\frac{2GM}{r c^2})^{-1} & 0 & 0 \\ 0 & 0 & r^2 & 0 \\ 0 & 0 & 0 & r^2 \sin^2 \theta \end{bmatrix}
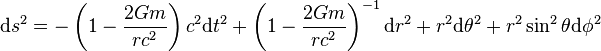
\mathrm ds^2=-\left(1-\frac{2Gm}{r c^2}\right)c^2\mathrm dt^2 + \left(1-\frac{2Gm}{r c^2}\right)^{-1}\mathrm dr^2+r^2\mathrm d \theta^2 + r^2 \sin^2 \theta \mathrm d \phi^2

Produit avec sa dérivée partielle

Le produit contracté du tenseur métrique et de sa dérivée partielle change de signe lorsqu'on remonte les indices d'un terme du produit et que l'on descend les indices de l'autre terme :

gijgij,k = − gijgij,k.

La matrice gij est l'inverse de la matrice du tenseur métrique gij :

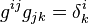
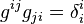
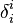
g^{ij} g_{jk} = \delta^i_k . Profitant de la symétrie du tenseur métrique, on a g^{ij} g_{ji} = \delta^i_i . Or la contraction \delta^i_i du tenseur unité donne un entier, la dimension de l'espace. C'est donc une constante. Ainsi gijdgij = − gijdgij. D'où l'expression cherchée.
  • Si gij,k était un tenseur, on aurait le signe +.
  • On a bien un tenseur en calculant la dérivée covariante gij;k du tenseur métrique, mais ce tenseur est nul.
Cas des coordonnées curvilignes
- Introduction - Définition - Coordonnées rectilignes - Pseudo-métrique - Montée et descente d'indices - Cas des coordonnées curvilignes - Changement de base - Distances et angles - Quelques exemples - Produit avec sa dérivée partielle
miniature
Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀
miniature
Record établi pour un transistor en diamant 💎
miniature
Les sursauts radio rapides trahissent enfin leur origine cosmique 📡
miniature
Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠
miniature
Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊
miniature
Les oscillations collectives des foules humaines denses 🔁
miniature
Une forme inconnue de la matière détectée au LHC ? ⚛️
miniature
Le sel, un facteur méconnu de l'obésité ? 🧂
miniature
L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀
miniature
Découverte tectonique majeure sous les Petites Antilles 🌍
miniature
1
Peut-on geler en chauffant ? ❄️
miniature
Une peau électronique pour doter les robots du sens du toucher 👌
miniature
Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳
miniature
Le cancer inscrit dans nos gènes dès la naissance ? 🧬
miniature
Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥
miniature
Le passé verdoyant du plus grand désert du monde 🐪
miniature
Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷
miniature
Des puces quantiques plus proches que jamais ⚡
miniature
1
Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬
miniature
En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊
miniature
Des scientifiques parviennent à produire efficacement du carburant à partir de monoxyde de carbone 🛢️
miniature
Que nous apprend la découverte de cet insecte de 16 millions d'années ? 🐜
miniature
Avec 91km, l'accélérateur FCC fera passer le LHC pour un jouet ⚛️
miniature
Cette vitamine développe les fonctions cognitives du cerveau 🧠
miniature
Comment des impacts géants vaporisent les corps planétaires ☄️
miniature
Les Américains riches vivent moins longtemps que les Européens pauvres 💰
miniature
Attention à ce riz naturellement riche en arsenic 🍚
miniature
L'intelligence artificielle contre la mort subite 💀
miniature
L'inévitable formation d'un océan de magma basal sur Terre 🔥
miniature
Découverte d'une plante étrange sans chlorophylle 🌱
miniature
Existe-t-il des mélodies naturelles ? 🎶
miniature
Cette exoplanète présente une signature de vie bien plus forte que celle de la Terre 👽
miniature
L'origine énigmatique des rayons cosmiques les plus énergétiques ⚡
miniature
1
Le diagnostic de l'autisme remis en cause par l'intelligence artificielle 🩺
miniature
Imprimer en 3D avec la lumière du soleil ☀️
miniature
La pollution atmosphérique nuit gravement au cerveau 🧠
miniature
Le trou noir supermassif Ansky vient de se réveiller ⚫
miniature
1
Voici ce qui rend notre cerveau vraiment unique 🧠
miniature
Asymétrie matière-antimatière: une nouvelle pièce du puzzle dévoilée 🧩
miniature
Neige en inuit, goût en japonais... comment les langues décomposent la réalité ? 💬
miniature
La physique révèle les secrets d'un strike parfait au bowling 🎳
miniature
Le TDAH associé à la démence 🧠
miniature
Découverte d'une nouvelle forme d'intrication quantique, une première en 20 ans ⚛️
miniature
Le régime cétogène montre des surprises sur le cholestérol 🧐
miniature
Un tango observationnel révèle une Super-Terre 🔭
miniature
Cette expérience montre que la graisse brune augmente fortement la longévité 🕒
miniature
1
L'Univers comme jamais vu auparavant: les révélations du fond diffus cosmologique 🔭
miniature
C'est sérieux: de la bave pourrait révolutionner la conception de bioplastiques 🪱
miniature
Découverte: le trou noir central de notre galaxie pourrait anéantir la vie sur Terre 💥
miniature
Etude scientifique: ces aliments nous font vieillir 🍽️
Page générée en 0.114 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise