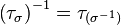Tenseur (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Produit tensoriel d'espaces vectoriels de dimensions finies
Il est pratique, avant d'étudier le produit tensoriel de vecteurs et de donner un sens plus précis au terme tenseur, de considérer les espaces vectoriels qui interviennent dans sa définition. On note que le même symbole, à savoir
On notera par la suite
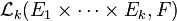
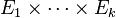
Définitions
Soit E et F deux espaces vectoriels de dimension finie sur un corps
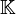


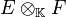
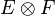
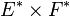
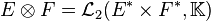
On rappelle par ailleurs qu'en dimension finie, on assimile sans problème E à son bidual E * * . On a donc de même :
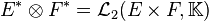
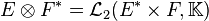
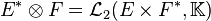
Dans la théorie des catégories, les
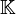
Propriétés
- Associativité
- Les ensembles
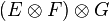
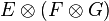

-
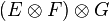
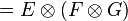
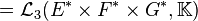
-
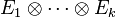
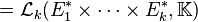
- Dimension
- La dimension d'un produit tensoriel d'espaces est égale au produit des dimensions de tous les espaces.
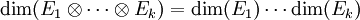
- Le corps des scalaires
-
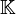
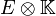
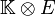
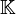
-
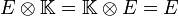
- Puissances tensorielles
- On peut définir la k-ième puissance tensorielle d'un espace E, notée
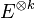
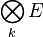
- pour
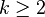
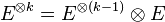
- pour k = 1, en extrapolant les définitions précédentes,
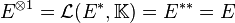
- pour k = 0, le choix de
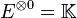
- pour
- On a par ailleurs les propriétés :
-
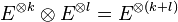
-
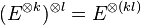
- Dualité
- Encore une fois par isomorphisme canonique on a :
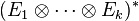
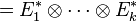
- Ensemble des applications linéaires et multilinéaires
- L'ensemble
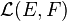
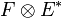
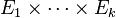
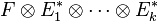
- À propos de la commutativité
- Il existe un isomorphisme entre
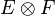
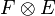
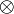
- Dans la suite de cet article on considérera donc, sauf mention contraire,
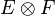
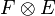
Permutation d'indices
Les espaces
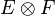
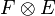
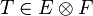
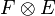
![\forall u \in E, \forall v \in F, \quad \left[ \tau_{(12)} T \right] (v,u) = T(u,v)](https://static.techno-science.net/illustration/Definitions/autres/a/a44d47a11053892e4de5795f5fc5c37d_05da811dae6b75be0093b3ea161ed0d9.png)
Ce principe se généralise pour k espaces. Soit
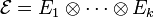
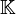
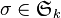
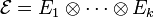
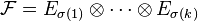
![\forall v_i \in E_i, \quad \left[ \tau_\sigma T \right] (v_{\sigma(1)},\cdots,v_{\sigma(k)}) = T(v_1,\cdots,v_k)](https://static.techno-science.net/illustration/Definitions/autres/6/60c28dfb1a6876485b65138271f3db01_8c416d579fffac335cbd715ee6ab6468.png)
On voit bien qu'une permutation induit naturellement un isomorphisme entre les espaces
Pour des raisons de commodité, on peut utiliser la notation canonique des permutations consistant à n'indiquer que la liste différentes permutations circulaires. Ainsi l'application τ(125) transforme l'indice 1 en l'indice 2, l'indice 2 en l'indice 5, l'indice 5 en l'indice 1 et laisse invariant les autres indices.
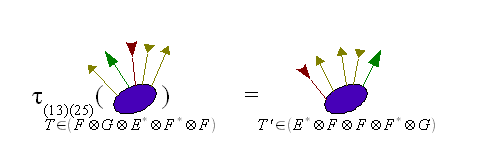
En théorie des catégories, ce type d'applications, qui fournit une notion proche de la commutativité, est étudié dans le cadre des catégories monoïdales tressées.
Non unicité de l'isomorphisme
Pour des espaces
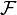
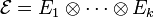
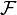
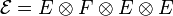
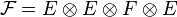
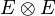
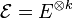
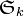
C'est cette absence d'unicité dans le cas général qui oblige à tenir compte de l'ordre des indices. De fait, on s'abstient en règle générale de considérer le produit tensoriel d'espaces comme commutatif.
Propriétés
- Transposition
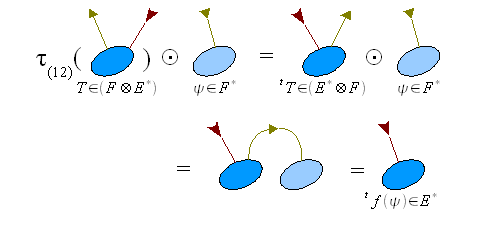
- Dans le cas de produit de deux espaces, l'application τ(12) peut être appelée transposition. Cette notion est cohérente avec celle de transposition d'application linéaire. On sait en effet qu'une application linéaire f de E dans F peut être représentée par un tenseur
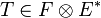
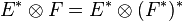
- Composition et inverse
- Pour deux permutations σ et σ' de
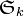
-
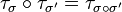
-