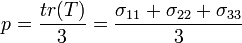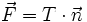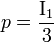Tenseur des contraintes - Définition

Pression isostatique

La pression isostatique p est définie comme le tiers de la trace de la matrice, c'est-à-dire comme la moyenne des termes diagonaux :

Sa valeur ne dépend pas du repère x y z utilisé.

C'est une généralisation de la notion de pression hydrostatique dans les liquides. Dans le cadre de la géophysique, on parle de pression lithostatique. Toutefois, dans ces cas-là, on considère -p : une contrainte de compression a une valeur négative, p est donc négatif dans ces cas-là.

Symétrie du tenseur des contraintes

Le tenseur des contraintes est toujours symétrique, c'est-à-dire que :

σ_i j = σ_j i

ce qui traduit l'équilibre en moment d'un volume infinitésimal.

Le tenseur s'écrit donc :

.

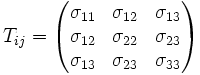
Du fait de cette symétrie, on peut écrire le tenseur comme un vecteur, selon la notation de Voigt : en définissant

• σ₁ = σ₁₁, σ₂ = σ₂₂, σ₃ = σ₃₃ ;
• σ₄ = σ₂₃, σ₅ = σ₃₁, σ₆ = σ₁₂ ;

On peut alors mettre le tenseur sous la forme :

.

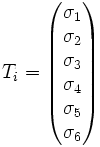
Ceci facilite l'écriture de la loi de Hooke généralisée. On voit aussi que l'espace des contraintes est un espace vectoriel à six dimensions.

Calcul des vecteurs-contrainte

Considérons le petit élément de volume dτ délimité par le tétraèdre de sommets M,(dx₁,0,0),(0,dx₂,0),(0,0,dx₃). Les vecteurs normaux aux faces sont donc . La force s'exerçant sur une face vérifie

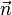
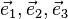
où le vecteur caractéristique de la face, c'est-à-dire le vecteur normal ayant pour norme l'aire de la face.

On a par exemple sur la face [M,(dx₁,0,0),(0,dx₂,0)], la relation

Principe de la coupure

Une manière simple de déterminer le tenseur des contraintes consiste à employer le « principe de la coupure ». Il s'agit d'une opération de pensée dans laquelle on scie l'objet selon un plan donné.

Supposons un solide se déformant sous l'effet de deux forces extérieures opposées. Si l'on coupe le solide en deux et que l'on sépare les moitiés, alors chaque moitié n'est soumise qu'a une seule force et donc n'est plus déformée mais mise en mouvement. Pour que chaque moitié retrouve sa déformation, il faut exercer une pression sur chacune des faces de la coupure.

Lorsqu'il y a des symétries évidentes à un problème, le choix de plans de coupe judicieux permet de déterminer de manière simple le tenseur des contraintes. C'est ainsi que l'on peut déterminer que dans le cas de la torsion d'un tube, on a un cisaillement pur.

Invariants du tenseur des contraintes

Les contraintes principales permettent de déterminer les invariants du tenseur :

 ;

 ;

.

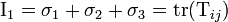
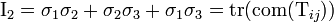
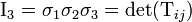
Notons que l'on a :

Contraintes principales

Il existe (au moins) une base orthonormée de l'espace dans laquelle le tenseur des contraintes est une matrice diagonale :

.

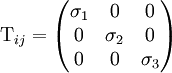
Ceci résulte de la symétrie de ce tenseur. Les valeurs σ₁, σ₂ et σ₃ sont appelées contraintes principales (il ne faut pas les confondre avec les contraintes en notation de Voigt).

Déviateur

Le tenseur des contraintes peut se décomposer en une somme de deux tenseurs : le déviateur (s_ij ) et la pression isostatique p⋅(δ_ij ) :

.

Le déviateur a les mêmes directions principales que le tenseur des contraintes, on a alors dans ce repère :

.

On peut définir des invariants pour le déviateur :

J₁ = s₁ + s₂ + s₃ = tr(s_ij) = 0 ;

J₂ = − s₁s₂ − s₂s₃ − s₁s₃ ;

J₃ = s₁s₂s₃ = det(s_ij).

Notons que l'on a aussi :

J₁ = s₁₁ + s₂₂ + s₃₃ ;

 ;

.

Ces invariants sont utiles pour définir le domaine élastique et le contrainte de comparaison.