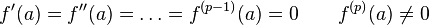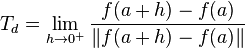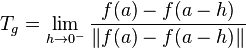Tangente (géométrie) - Définition

Calculs de tangente

Tangente à un graphe de fonction numérique

Ici f est une fonction définie sur un intervalle de la forme ]a − α,a + α[,α > 0, à valeurs réelles. On se préoccupe de savoir si le graphe, d'équation y=f(x), admet une tangente au point A de coordonnées (a,f(a)).

La sécante entre les points d'abscisse a et a+h est la droite passant par A et de pente , qui est un taux de variation de f. Il y a trois possibilités

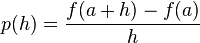
• si p(h) admet une limite finie p lorsque h tend vers 0, il y a une tangente : la droite passant par A et de pente p. La fonction est alors dérivable et la pente de la tangente est la valeur de la dérivée.

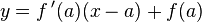
  L'équation de cette tangente est alors

• si p(h) admet une limite infinie, il y a une tangente : la droite d'équation x=a.

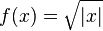
  Cela se produit par exemple pour la fonction

• sinon (si la limite est indéterminée), pas de tangente.

Tangente à un arc paramétré

Cette fois f est une fonction définie sur un intervalle de la forme ]a − α,a + α[,α > 0 à valeurs dans un espace vectoriel E de dimension finie. On fait l'étude au voisinage du point de paramètre a.

Une première condition pour pouvoir parler de sécante est que au voisinage de a, la courbe ne passe qu'une fois par le point a. Dans ce cas, on peut de nouveau calculer la pente de la sécante et chercher si elle a une limite.

En tout cas, la notion de tangente ne dépend pas du paramétrage choisi. Pour le prouver, il s'agit simplement d'appliquer un théorème de composition de limites.

Lien avec le calcul différentiel

Si f admet un vecteur dérivé non nul au point a, on dit que a est un point régulier et il y a une tangente, dirigée par le vecteur f'(a).

Si f admet une succession de dérivées nulles en a puis une première dérivée non nulle en allant à l'ordre p

alors il y a une tangente, dirigée par la première dérivée non nulle. En un tel point on dit qu'il y a un contact d'ordre p entre la courbe et sa tangente (alors qu'en un point régulier le contact est seulement d'ordre 1).

Attention : la tradition française est d'utiliser le mot «régulier» pour deux concepts distincts, la régularité de f comme fonction ou celle de l'arc. Il est possible de paramétrer un carré de façon , ce qui montre bien que la régularité au sens des fonctions ne donne pas nécessairement l'existence de tangentes. Simplement, pour un tel paramétrage, aux sommets, toutes les dérivées seront nulles.

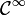
Demi-tangentes

Pour une étude plus précise, on peut introduire des demi-tangentes à droite et à gauche pour définir le comportement pour les valeurs du paramètre strictement supérieures ou strictement inférieures à a. L'information supplémentaire contenue dans une demi-tangente est le sens du mouvement.

On dit qu'il y a une demi-tangente à droite quand la limite suivante existe

La demi-tangente est alors la demi-droite d'origine ce vecteur T_d.

On dit qu'il y a une demi-tangente à gauche quand la limite suivante existe (attention à l'ordre)

La demi-tangente est alors la demi-droite d'origine ce vecteur T_g.

S'il y a des demi-tangentes, on utilise le vocabulaire suivant :

• point anguleux quand les demi-tangentes forment un angle non plat

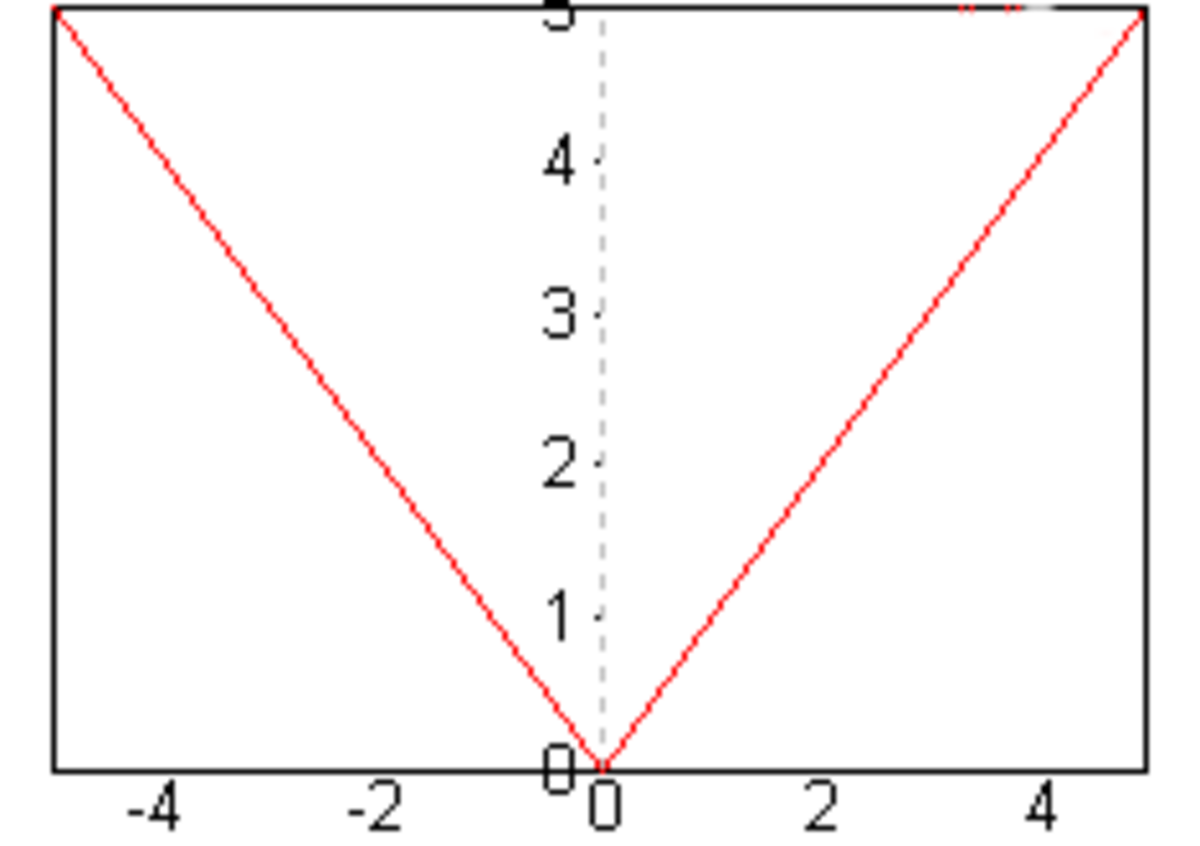
Le graphe de la fonction valeur absolue donne un exemple de point anguleux

• point de rebroussement quand les demi-tangentes sont opposées : il y a alors une tangente, mais la courbe fait une sorte de demi-tour, d'où le nom.

Dans le cas d'une deltoïde, on voit trois points de rebroussement.

• tangente sans rebroussement pour le cas le plus fréquent : les demi-tangentes sont égales.

Courbe en coordonnées polaires

Si l'arc admet pour paramètre l'angle polaire ρ(θ), le vecteur dérivé admet pour expression dans la base mobile ρ'(θ)u(θ) + ρ(θ)v(θ).

• tous les points autres que l'origine sont réguliers, et possèdent donc une tangente
• si l'arc passe par l'origine en θ₀, alors la sécante M₀M(θ) n'est autre que la droite d'angle θ. Il y a donc toujours une tangente : la droite d'angle θ₀.

En toute rigueur, pour que les sécantes existent il faut ajouter la condition que l'arc ne passe qu'une fois par l'origine pour θ assez petit.

Tangente pour une courbe implicite

On considère une courbe d'équation cartésienne f(x,y)=C dans le plan euclidien, pour une fonction f de classe sur un ouvert du plan.

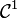
Le théorème des fonctions implicites permet de se ramener à un arc paramétré et de déterminer existence et équation éventuelle de la tangente à cette courbe en un point donné. Précisément, un point M=(x,y) appartenant à la courbe est dit régulier quand le gradient de f est non nul en ce point. Et dans ce cas, la tangente est orthogonale au vecteur gradient.