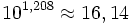Table de logarithmes - Définition

Utilisation d'une table de logarithme

Lecture

De simples tables de logarithmes à cinq décimales sont généralement développées de telle sorte que les nombres formés des deux premiers chiffres (de 10 à 99) forment le bord gauche du tableau, tandis que les derniers chiffres (de 0 à 9) apparaissent en tête de colonne.

Une table de logarithmes se présente sous la forme suivante :

N    0    1    2    3   … 9
10 0000 0043 0086 0128  …
11 0414 0453 0492 0531  …
12 0792 0828 0864 0899  …
13 1139 1173 1206 1239  …
14 1461 1492 1523 1553  …
15 1761 1790 1818 1847  …
16 2041 2068 2095 2122  …
17 2304 2330 2355 2380  …
18 2553 2577 2601 2625  …
19 2788 2810 2833 2856  …
.    .    .    .    .
.    .    .    .    .
.    .    .    .    .
99

Ici, le chiffre des unités et celui des dixièmes du nombre N figurent dans la colonne de gauche et le chiffre des centièmes dans la première ligne. À l'intersection d'une ligne et d'une colonne, on lit log(N).

Exemple 1 : Comment déterminer log(1,53) ?

On se place dans la ligne 15 et dans la colonne 3 et on lit 1847. On peut donc conclure que

log(1,53) 0,1847

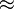
Exemple 2 : Comment déterminer log(0,00153) ?

On sait que la caractéristique de ce nombre est -3 et que sa mantisse est log(1,53).

Donc log(0,00153) = -3 + 0,1847 -2,8153

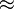
Exemple 3 : Comment déterminer log(18,27) ?

On sait que sa caractéristique est 1 et que sa mantisse est log(1,827). On se place donc dans la ligne 18 et entre la colonne 2 et la colonne 3. Il faut alors faire une interpolation linéaire

log(1,82) 0,2601 et log(1,83) 0,2625 soit une différence de 24 dix-millièmes. L'interpolation linéaire permet d'approcher les logarithmes des nombres compris entre 1,82 et 1,83 de la manière suivante

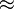
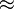
log(1,821) 0,2601 + 0,00024

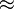
log(1,822) 0,2601 + 0,00048

…

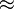
log(1,827) 0,2601 + 7 × 0,00024 0,2618

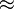
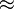
log(18,27) 1,2618

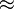
Exemple 4: Quel est le nombre dont le logarithme est 1,208 ?

On sait que la caractéristique est 1 et que le nombre s'écrit donc N.10 avec log(N) = 0,208

Dans la table de logarithmes 2080 est compris entre 2068 et 2095 (différence de 27). 2068 est dans la ligne des 16 et dans la colonne des 1 donc 0,2068 = log(1,61). De même 0,2095 = log(1,62). On procède donc encore à une interpolation linéaire

0,2068 + 0,00027 = 0,20707 = log(1,611)

0,20707 + 0,00027 = 0,20734 = log(1,612)

…

0,2068 + 4 × 0,00027 = 0,20788 = log(1,614)

0,2068 + 5 × 0,00027 = 0,20815 = log(1,615)

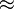
0,208 log(1,614)

Calculs