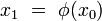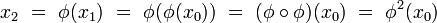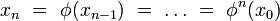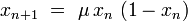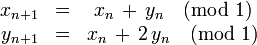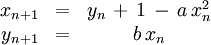Système dynamique - Définition

Introduction

En mathématiques, en physique théorique et en ingénierie, un système dynamique est un système classique qui évolue au cours du temps de façon à la fois :

• causale, c’est-à-dire que son avenir ne dépend que de phénomènes du passé ou du présent ;
• déterministe, c’est-à-dire qu'à une « condition initiale » donnée à l'instant « présent » va correspondre à chaque instant ultérieur un et un seul état « futur » possible.

On exclut donc ici conventionnellement les systèmes « bruités » intrinsèquement stochastiques, qui relèvent de la théorie des probabilités.

L'évolution déterministe du système dynamique peut alors se modéliser de deux façons distinctes :

• une évolution continue dans le temps, représentée par une équation différentielle ordinaire. C'est a priori la plus naturelle physiquement, puisque le paramètre temps nous semble continu.
• une évolution discontinue dans le temps. Ce second cas est souvent le plus simple à décrire mathématiquement, même s'il peut sembler a priori moins réaliste physiquement. Cependant, l'étude théorique de ces modèles discrets est fondamentale, car elle permet de mettre en évidence des résultats importants, qui se généralisent souvent aux évolutions dynamiques continues.

Système dynamique à temps discret

Notion d'état dynamique : aspect philosophique

Il faut faire attention au sens très particulier que prend la notion d’état pour la théorie des systèmes dynamiques. Un paradoxe de Zénon permet de présenter la difficulté. Zénon demandait : « Soit une flèche en vol. À un instant, est-ce qu’elle est au repos ou en mouvement ? » Si on répondait qu’elle est en mouvement, il disait « Mais être en mouvement, c’est changer de position. À un instant, la flèche a une position, elle n’en change pas. Elle n’est donc pas en mouvement. » Si on répondait qu’elle est au repos, il disait « Mais si elle est au repos à cet instant, elle est aussi au repos à tous les autres instants, elle est donc toujours au repos. Elle n’est jamais en mouvement. Mais comment alors peut-elle passer d’une position à une autre ? » Il en concluait qu’il n’est pas possible de dire des vérités sur ce qui est en mouvement. Tout ce qui est en mouvement serait par nature mensonger et il n’y aurait pas de vérités à propos de la matière mais seulement à propos des grandes idées, pourvu qu’elles soient immuables. Le sens commun est exactement inverse. On croit plus couramment à la vérité de ce qu’on voit qu’aux vérités métaphysiques. La théorie des systèmes dynamiques rejoint le sens commun sur ce point.

La notion d’état dynamique fournit une solution au paradoxe de Zénon : à un instant, la flèche est en mouvement, elle a une position mais elle est en train de changer de position, elle a une vitesse instantanée. Les nombres qui mesurent sa position et sa vitesse sont les valeurs de ses variables d’état. Les variables d’état sont toutes les grandeurs physiques qui déterminent l’état instantané du système et qui ne sont pas constantes a priori. On les appelle aussi les variables dynamiques. Si on prend une photo au flash on ne voit pas que la flèche est en mouvement, mais on peut le détecter par d’autres moyens, par l’effet Doppler par exemple, sans avoir à mesurer un changement de position. L’état dynamique d’un système est un état instantané, mais c’est un état de mouvement. Il est déterminé par les valeurs de toutes les variables d’état à cet instant.

Espace des phases

Pour un système possédant n degrés de liberté, l'espace des phases Γ du système possède n dimensions, de telle sorte que l'état complet du système à l'instant t est en général un vecteur à n composantes.

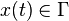
Dynamique discrète

Un système dynamique discret est défini par une application bijective de l'espace des phases sur lui-même. Elle opère de la façon suivante : étant donnée une condition initiale x₀ de l'état du système, le premier état suivant est :

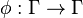
Le second état, qui suit immédiatement le premier, est :

et ainsi de suite, de telle sorte que le n-ième état est donné par :

Pour remonter dans le passé, il suffit d’inverser la fonction φ, ce qui est toujours possible pour une bijection.

Classification des dynamiques

On distingue plusieurs grands types de dynamiques en fonction de la nature mathématique de l'espace des phases :

• lorsque Γ est un espace topologique et l'application un homéomorphisme, on parle de dynamique topologique.

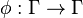
• lorsque Γ est une variété différentielle et l'application un difféomorphisme, on parle de dynamique différentielle.

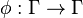
• lorsque Γ est un espace mesuré et une application qui préserve la mesure, on entre dans le domaine de la théorie ergodique, et on parle de système dynamique mesuré

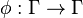
Exemples

La fonction logistique

La fonction logistique est une application du segment [0, 1] dans lui-même qui sert de récurrence à la suite :

où n = 0, 1, ... dénote le temps discret, x l'unique variable dynamique, et un paramètre.

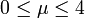
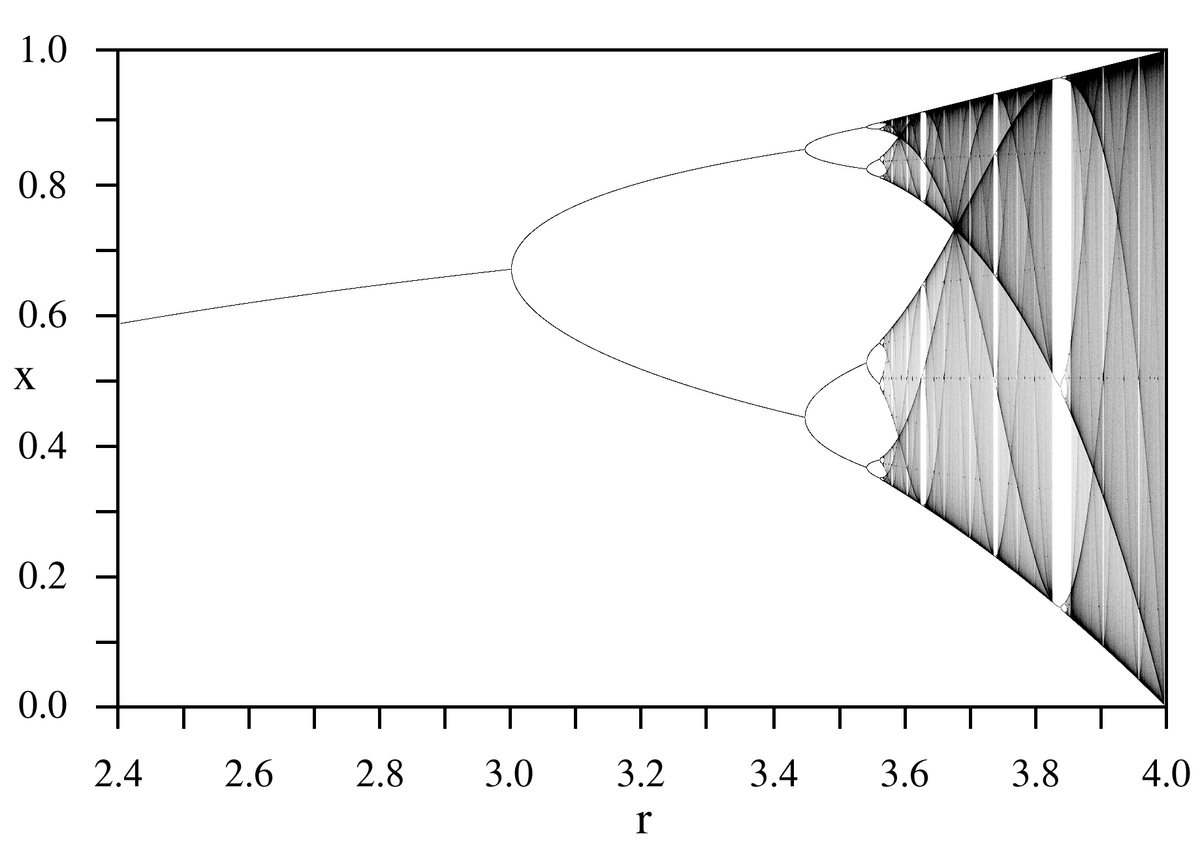
La dynamique de cette application présente un comportement très différent selon la valeur du paramètre μ :

• Pour , le système possède un point fixe attractif, qui devient instable lorsque μ = 3.

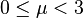
• Pour , l'application possède un attracteur qui est une orbite périodique, de période 2ⁿ où n est un entier qui tend vers l'infini lorsque μ tend vers 3,57 ...

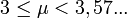
• Lorsque μ = 3,57..., l'application possède un attracteur de Feigenbaum fractal (mais non étrange) découvert par May (1976).

• Le cas μ = 4 avait été étudié dès 1947 par Ulam et von Neumann. On peut dans ce cas précis établir l'expression exacte de la mesure invariante ergodique.

On obtient donc une succession de bifurcations de la régularité vers le chaos lorsque le paramètre augmente, résumée sur la figure ci-jointe.

L'application « chat » d'Arnold (1968)

Le nom d'application « chat » provient d'un jeu de mot anglais intraduisible en français : en effet, « chat » se dit « cat » en anglais, et Arnold utilisait ce mot comme abréviation de : « Continuous Automorphisms of the Torus », littéralement : « automorphismes continus sur le tore ».

L'application « chat » est une application du carré [0, 1] x [0, 1] dans lui-même définie par :

où mod 1 signifie : modulo 1. Cette condition entraine que le carré [0, 1] x [0, 1] voit ses bords recollés deux à deux pour former le « tore » du titre. Il s'agit d'un système dynamique conservatif, qui préserve la mesure de Lebesgue dx dy.

L'application de Hénon (1976)

L'application de Hénon est une bijection du carré [0, 1] x [0, 1] dans lui-même définie par :

où a et b sont deux paramètres, dont des valeurs typiques sont a = 1,4 et b = 0,3. Avec ces valeurs, la dynamique présente un attracteur étrange de nature fractale, de type Cantor.

Hénon a obtenu ses équations en cherchant une version simplifiée du système dynamique de Lorenz à temps continu introduit en 1963 (cf. plus bas). Le système dynamique de Hénon n'est pas conservatif, car le jacobien de la transformation est constant et vaut - b, qui est différent de l'unité dans les cas intéressants.

Autres exemples

• La dynamique holomorphe, où l'espace des phases est le plan complexe et φ une application holomorphe. Une telle dynamique est par exemple à l'origine de l'ensemble de Mandelbrot.

• La percolation