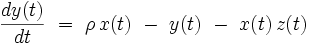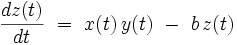Système dynamique - Définition
La liste des auteurs de cet article est disponible ici.
Systèmes linéaires et Systèmes non linéaires
Nous distinguons les systèmes dynamiques linéaires des systèmes dynamiques non-linéaires. Dans les premiers, le membre de droite de l'équation est une fonction dépendant linéairement de x, telle que:
La somme de deux solutions d'un système linéaire est également solution (« principe de superposition »). Les solutions d'une équation linéaire forment un espace vectoriel, ce qui permet l'utilisation de l'algèbre linéaire et simplifie considérablement l'analyse. Pour les systèmes à temps continu, la transformée de Laplace permet de transformer les équations différentielles en des équations algébriques.
Les deux premiers exemples donnés plus haut sont des systèmes non linéaires. Leur analyse est en général très difficile. Par ailleurs, les systèmes non linéaires ont souvent des comportements dits chaotiques, ce qui les rend apparemment imprévisibles.
Système dynamique différentiel
Depuis Newton (1687), l'idée que l'évolution temporelle d'un système physique quelconque est bien modélisée par une équation différentielle (ou ses généralisations à la théorie des champs, les équations aux dérivées partielles) est admise. Cette modélisation différentielle s'est depuis étendue avec succès à d'autres disciplines comme la chimie, la biologie, l'économie, ...
Pour un système possédant n degrés de liberté, l'espace des phases Γ du système possède n dimensions, de telle sorte que l'état complet
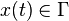
|
|
où la fonction f définit le système dynamique étudié (c'est en général également un vecteur à n dimensions, c’est-à-dire un ensemble de n fonctions scalaires).
Problème de Cauchy
On se pose la question suivante, appelée problème de Cauchy : étant donnée une condition initiale x0 représentant l'état complet du système physique dans son espace des phases à un instant initial t0, trouver l'état complet du système x(t) dans son espace des phases pour tout instant ultérieur t > t0. La solution à ce problème fondamental réside dans le théorème de Cauchy-Lipschitz, qui assure l'existence locale et l'unicité de la solution d'une équation différentielle.
Déterminisme
L’hypothèse que l’avenir est déterminé par le présent est très audacieuse. Son succès n’est pas a priori évident. Pourtant toutes les grandes théories fondamentales de la physique l’ont adoptée, à la suite de Newton.
Déterminisme d'un système conservatif
Nous conviendrons de dire qu'un système physique conservatif est déterministe si et seulement si la dynamique du système associe à chaque condition initiale x0 un et un seul état final x(t). Il faut pour cela qu'il existe une application bijective
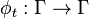
|
|
Lorsque le temps t varie, cette bijection engendre un flot sur Γ, c’est-à-dire un groupe continu à un paramètre φt tel que :
|
|
Cette description correspond par exemple au flot hamiltonien de la mécanique classique, ainsi qu'au flot géodésique.
Cas d'un système non-conservatif
Lorsque le système physique considéré est non-conservatif, l'application φt n'est pas bijective, et il existe en général un (ou plusieurs) attracteur dans l'espace des phases du système, c’est-à-dire un sous-ensemble de l'espace des phases invariant sous φt vers lequel converge le point représentatif x(t) du système lorsque le temps t tend vers l'infini, et ce pour presque toute condition initiale x0.
Exemples
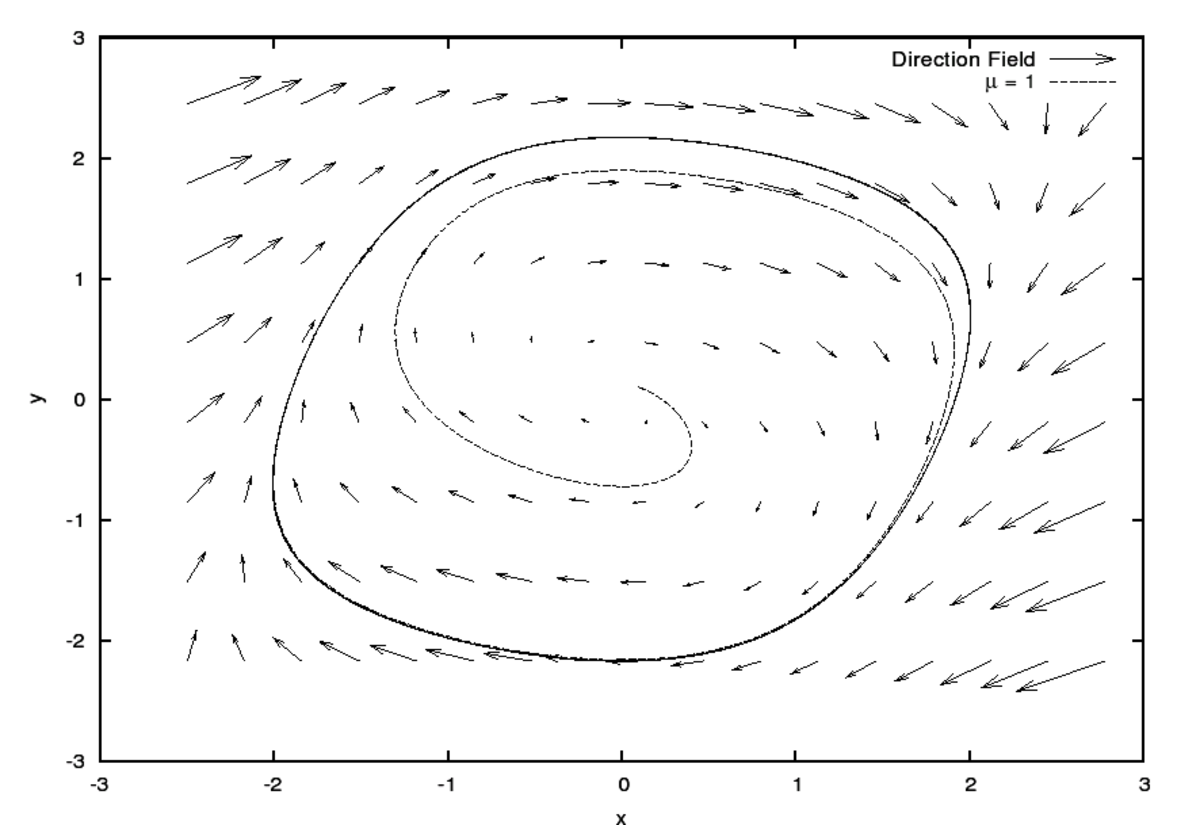
L'oscillateur de Van der Pol (1928)
L'oscillateur de van der Pol libre (i.e. sans excitation extérieure) est un système à un degré de liberté, décrit par la coordonnée x(t), qui possède deux paramètres :
- une pulsation ω0
- un coefficient de non-linéarité ε.
Son équation différentielle s'écrit :
|
|
Ce système dissipatif possède une dynamique régulière lorsqu'il est libre, caractérisée par un attracteur en forme de cycle limite représenté sur la figure ci-dessous (où on a posé ω0 = 1) :
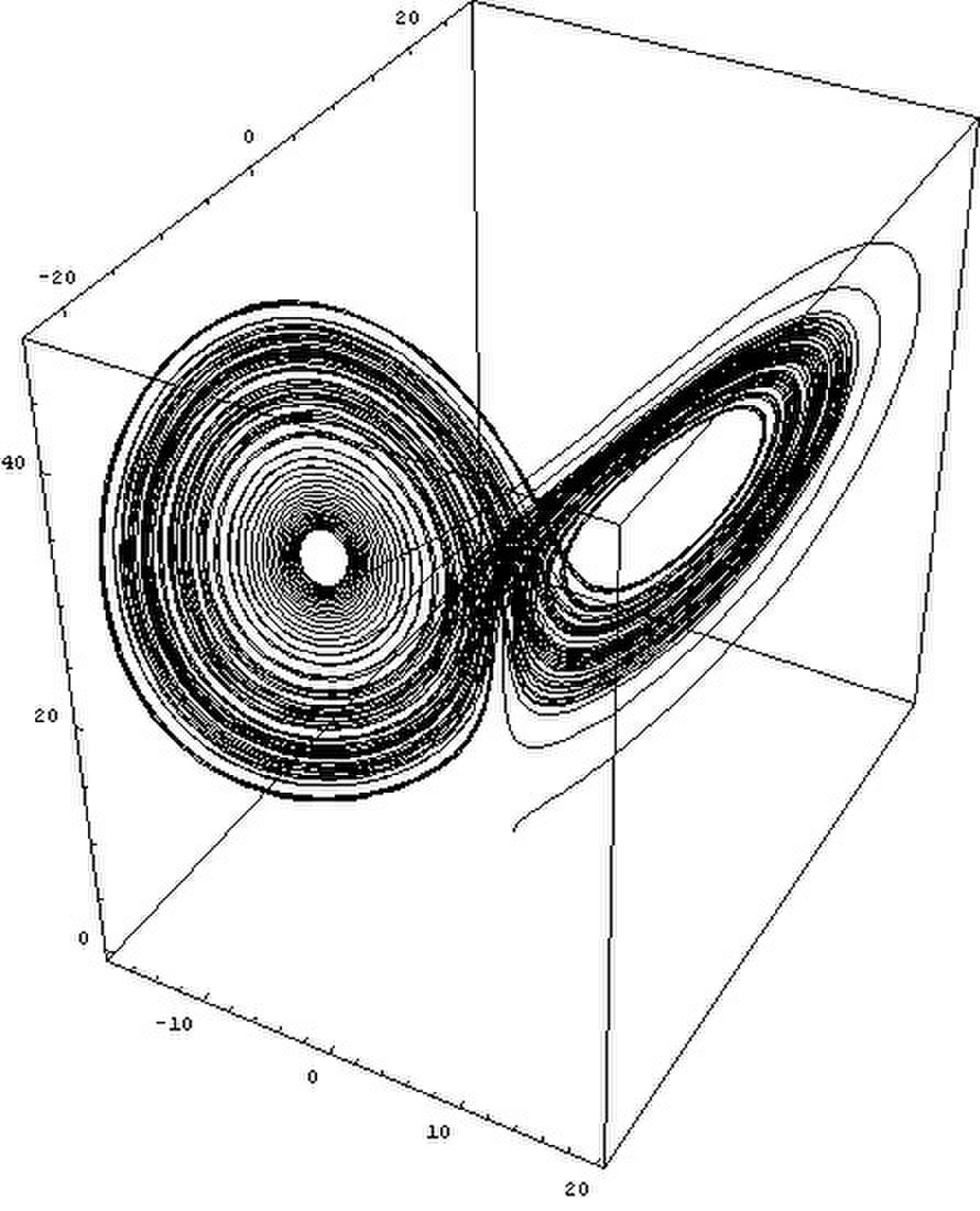
Le système de Lorenz (1963)
En 1963, Lorenz a proposé un système différentiel possédant trois degrés de liberté., notés x(t), y(t) et z(t), qui s'écrit :
|
|
|
|
|
|
Dans ces équations, σ, ρ et b sont trois paramètres réels. Pour les valeurs suivantes : σ = 10, ρ = 28 et b=8/3, ce système dynamique différentiel présente un superbe attracteur étrange, représenté sur la figure ci-jointe.
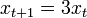
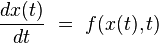
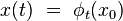
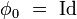
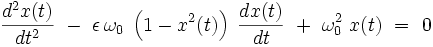
![\frac{dx(t)}{dt} \ = \ \sigma \ \left[ \ y(t) - x(t) \ \right]](https://static.techno-science.net/illustration/Definitions/autres/b/beda9b7e28158bdcb1119bba208e0b5b_46c01386118d5918498bbc1d687a50bd.png)