Système d'équations (mathématiques élémentaires) - Définition
La liste des auteurs de cet article est disponible ici.
Définitions mathématiques
On appelle système d'équations un ensemble
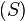
Exemple :
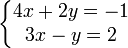
Résoudre
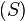
Le système
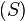
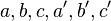
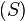
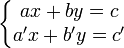
Système de 3 équations à 3 inconnues
Les systèmes de 3 équations à 3 inconnues se résolvent aussi de cette manière :
Méthode par substitution
-
![\left\{\begin{matrix} x+10y-3z=5 \quad[1] \\ 2x-y+2z=2 \quad[2] \\ -x+y+z=-3 \quad[3] \end{matrix}\right.](https://static.techno-science.net/illustration/Definitions/autres/c/c5839baae05cad180709721d5624bd51_2b2f72407be7e0574a45c0f9e0e83534.png)
Pour résoudre ce système de 3 équations à 3 inconnues, on isole une inconnue dans une des équations. Dans ce système, on isole l'inconnue x dans l'équation [1]
- [1] :
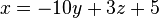
Maintenant on remplace l'inconnue
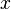
-
![\left\{\begin{matrix} 2(-10y+3z+5)-y+2z=2 [2] \\ -(-10y+3z+5)+y+z=-3 [3] \end{matrix}\right.](https://static.techno-science.net/illustration/Definitions/autres/0/0d72ef1c3af9f1d19f024a856fd583ca_f4d64e93addd86b8dfe598569bf7daca.png)
Après avoir trouvé
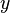
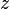
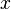
Méthode par élimination
-
![\left\{\begin{matrix} x+10y-3z=5 \quad[1] \\ 2x-y+2z=2 \quad[2] \\ -x+y+z=-3 \quad[3] \end{matrix}\right.](https://static.techno-science.net/illustration/Definitions/autres/c/c5839baae05cad180709721d5624bd51_2b2f72407be7e0574a45c0f9e0e83534.png)
Pour résoudre ce système, on peut éliminer
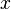
-
![\left\{\begin{matrix} x+10y-3z=5 \quad[1] \\ -21y+8z=-8 \quad[2'] \\ 11y-2z=2\quad[3'] \end{matrix}\right.](https://static.techno-science.net/illustration/Definitions/autres/9/98a63d59963034ea69dff064a268236c_ccae24df55f88505ba8c78f80eda0ea6.png)
Il suffit alors d'éliminer une autre inconnue,
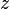
L'équation [3"] permet de trouver
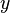
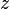
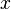
Cette méthode se généralise à des systèmes comportant davantage d'équations et davantage d'inconnues et prend le nom de méthode du pivot de Gauss.
![\left\{\begin{matrix} x+10y-3z=5 \quad[1] \\ -21y+8z=-8 \quad[2'] \\ 23y=0\quad[3''] \end{matrix}\right.](https://static.techno-science.net/illustration/Definitions/autres/5/52de18b453467277e7d3f3c9a91552e4_5bd62eecca35ff20815f8605ebb61ae0.png)

















































