Surface de Riemann - Définition

Introduction

En géométrie différentielle, une surface de Riemann est une variété complexe de dimension 1. Par oubli de structure, une surface de Riemann se présente comme une variété différentielle réelle de dimension 2, d'où le nom surface. Elles ont été nommées en hommage au mathématicien allemand Bernhard Riemann. Toute surface réelle orientable peut être munie d'une structure complexe, autrement dit être regardée comme une surface de Riemann. Cela est précisé par le théorème d'uniformisation.

L'étude des surfaces de Riemann est à la croisée de nombreux autres domaines mathématiques dont, hormis la géométrie différentielle, la théorie des nombres, la topologie algébrique, la géométrie algébrique, les équations aux dérivées partielles...

Théorie élémentaire

Définition

Une surface de Riemann est un espace topologique séparé X, admettant un atlas modelé sur le plan complexe C dont les applications de changement de cartes sont des applications biholomorphes. Autrement dit X admet un recouvrement par des ouverts U_i homéomorphes à des ouverts de C ; ces cartes dites holomorphes sont telles que les fonctions de changement de cartes soient des fonctions holomorphes entre ouverts de C.

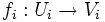
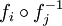
On peut ajouter de nouvelles cartes tant qu'elles sont compatibles avec les précédentes au sens où les applications de changement de carte restent holomorphes. De fait, il existe ainsi un atlas maximal pour la surface de Riemann. On identifiera deux structures de surface de Riemann sur un même espace topologique lorsqu'elles sont compatibles, c'est-à-dire conduisent au même atlas maximal.

Si X et Y sont deux surfaces de Riemann, une application de X dans Y est dite holomorphe lorsque, lue dans les cartes holomorphes, elle est holomorphe.

Le plan complexe C s'identifie naturellement à R². Comme holomorphe implique différentiable, toute surface de Riemann hérite d'une structure de variété différentielle de dimension 2. Comme toute application holomorphe préserve l'orientation de C, toute surface de Riemann hérite d'une orientation en tant que variété réelle. De fait :

Toute surface de Riemann se présente comme une surface réelle orientée.

Ces considérations se généralisent pour toutes les variétés holomorphes.

Par contre, toute variété différentielle réelle orientée de dimension paire n'admet pas forcément de structure complexe. C'est un fait remarquable en dimension 2, que toute surface réelle orientée admet effectivement une structure de surface de Riemann. Mais cette structure n'est pas forcément unique.

Contrairement à ce qui peut se produire pour des variétés réelles de dimension 1 (cf. la longue droite), les surfaces de Riemann sont toutes métrisables, séparables, paracompactes et σ-compactes ; il n'est donc pas nécessaire de poser une de ces conditions dans leur définition pour interdire des objets pathologiques. C'est un résultat dû à Tibor Radó (en).

Exemples

• Le plan complexe C se présente très simplement comme surface de Riemann. L'identité permet de définir un atlas réduit à une unique carte.

• Le plan complexe conjugué est topologiquement C, mais on le munit comme unique carte de la conjugaison complexe.

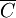
• La plus simple des surfaces de Riemann compactes est la sphère de Riemann, conformément équivalente à la droite projective complexe. Sa topologie est celle du compactifié d'Alexandroff du plan complexe, à savoir S² = C ∪ {∞}. Elle est recouverte de deux cartes holomorphes, définies respectivement sur C et C^*∪ {∞} : l'identité z z et l'inversion z 1/z.

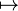
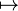
• Le plan projectif complexe P¹C est une autre représentation de la sphère de Riemann. Elle apparait comme le quotient de C²-{(0;0)} par l'action naturelle par multiplication du groupe (passage au quotient pour les variétés analytiques).

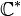
• Le plan hyperbolique est un exemple fondamental de surface de Riemann correspondant au disque ouvert de C, ou au demi plan supérieur, ou encore, par le théorème d'uniformisation, à tout ouvert simplement connexe de ( et différent de ).

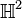
Pour juger de l'importance de ces exemples : Le revêtement universel de toute surface de Riemann connexe est une surface de Riemann simplement connexe isomorphe à , ou à ou à .

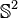
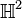
Par exemple : est le quotient du plan complexe par le groupe des translations . Plus précisément, le revêtement est donné par l'exponentielle complexe.

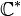
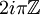
Surfaces hyperboliques

Le groupe projectif PGL₂(R) agit transitivement sur . Une surface hyperbolique est le quotient de par une action proprement discontinue et sans point fixe d'un sous-groupe discret Γ.

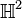
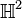
D'après la théorie des revêtements, le groupe fondamental de la surface obtenue X est isomorphe à Γ.

Si , la variété obtenue est orientable et peut être munie d'une structure de surface de Riemann.