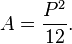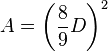Superficie - Définition
La liste des auteurs de cet article est disponible ici.
Histoire
Haute Antiquité
Selon Hérodote, la géométrie dans l'Égypte antique prend son origine dans la nécessité de répartir équitablement les surfaces des champs cultivés après les crues du Nil. Les Égyptiens connaissaient les formules usuelles de calcul des aires des polygones et la majorité des problèmes de géométrie conservés de cette époque concernent des problèmes d'aires.
À Babylone, l'aire A était calculée à partir du périmètre P d'un cercle suivant une procédure équivalente à la formule :
Même lorsqu'ils connaissaient le diamètre d'un cercle, les scribes passaient toujours par le calcul de son périmètre (en multipliant le diamètre par 3) pour ensuite obtenir son aire. La procédure était la suivante, comme dans cet exemple, extrait de la résolution d'un problème où il est demandé de déterminer le volume d'une bûche cylindrique dont le diamètre était 1 + 2⁄3 :
Méthode babylonienne — Triple 1 + 2⁄3, le dessus de la bûche, et 5, la circonférence de la bûche, viendra. Prends le carré de 5 et 25 viendra. Multiplie 25 par 1⁄12, la constante, et 2 + 1⁄12, l'aire, viendra.
![](https://static.techno-science.net/illustration/Definitions/1200px/c/calculation-of-pi-by-ahmes.svg_30dbcb01d2ffff61c3eb1ee820aa4445.png")
En Égypte, le calcul s'effectuait à partir du diamètre D :
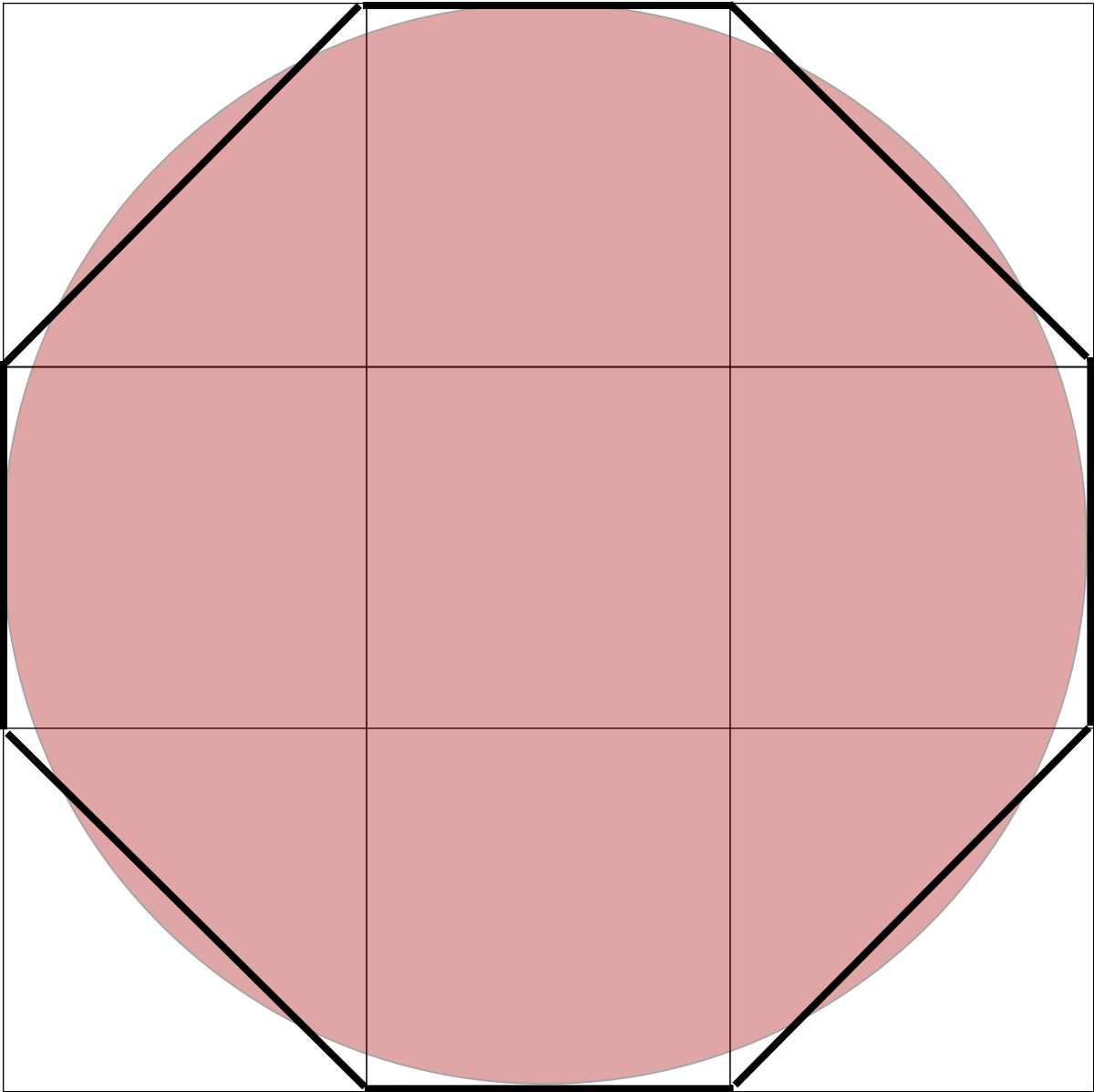
Le raisonnement consistait probablement à inscrire un octogone et un cercle dans un carré. La figure ci-contre illustre ce raisonnement : si le carré a pour côté le diamètre D du disque, l'octogone construit sur le tiers du côté du carré possède une aire de
.
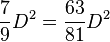
L'aire du disque est considérée comme légèrement supérieure à celle de l'octogone, soit
.
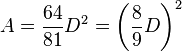
La Grèce antique
- Euclide, dans ses Éléments, démontre l'identité remarquable
- (a + b)2 = a2 + b2 + 2ab
par un raisonnement sur des aires de carrés.
- Héron d'Alexandrie (c. 100 ap. J.-C.) publie la formule permettant de calculer l'aire d'un triangle, connaissant ces trois côtés, et appelé formule de Héron. Mais cette formule était connue d'Archimède
Mathématiques arabes
Al-Khawarizmi, dans son Abrégé du calcul par la restauration et la comparaison, analyse et résout les équations du second degré par des considérations géométriques sur des aires de carrés, poursuivant en cela la tradition de l'algèbre géométrique remontant à l'Antiquité.