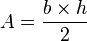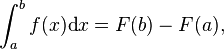Superficie - Définition
La liste des auteurs de cet article est disponible ici.
Calcul de l'aire
La figure de base pour le calcul d'une aire est le carré unité, de côté 1, suivie du rectangle. À l'aide de l'aire du rectangle, il est possible de déterminer l'aire d'un triangle rectangle (vu comme un demi-rectangle) ou d'un parallélogramme, puis celle d'un triangle et, par suite, d'un polygone quelconque.
La formule de l'aire d'un disque est plus complexe à démontrer : elle nécessite le passage par une limite de suite. L'idée d'approcher successivement une surface complexe par une suite de surfaces plus simples (en général, des rectangles ou des polygones) est fondamentale. Une surface qui peut être « correctement » approchée par des rectangles, au point qu'on puisse en déduire son aire par un calcul de limite est dite quarrable.
Dans certains cas, l'analyse vient au secours de la géométrie, lorsque les raisonnements par découpage et recollement ne suffisent plus. Certaines aires sont égales à des intégrales qui peuvent parfois être calculées à partir de primitives d'une fonction.
D'autres cas sont plus pathologiques : les mathématiciens ont établi une théorie de la mesure pour généraliser les résultats sur les aires. Pour les fractales, les aires ne sont pas calculables — ou non satisfaisantes. La notion de dimension de Hausdorff généralise celle d'aire, pour un objet fractal plan.
Surfaces usuelles
Ci-dessous sont données les formules de calcul d'aire usuelles les plus courantes et des démonstrations, qui illustrent les raisonnements géométriques souvent utilisés pour résoudre les problèmes d'aire : « coupé-collé », parfois en imaginant une infinité de découpages par des considérations sur les limites.
Rectangle
Aire d'un rectangle — L'aire d'un rectangle est égale au produit de sa longueur par sa largeur.
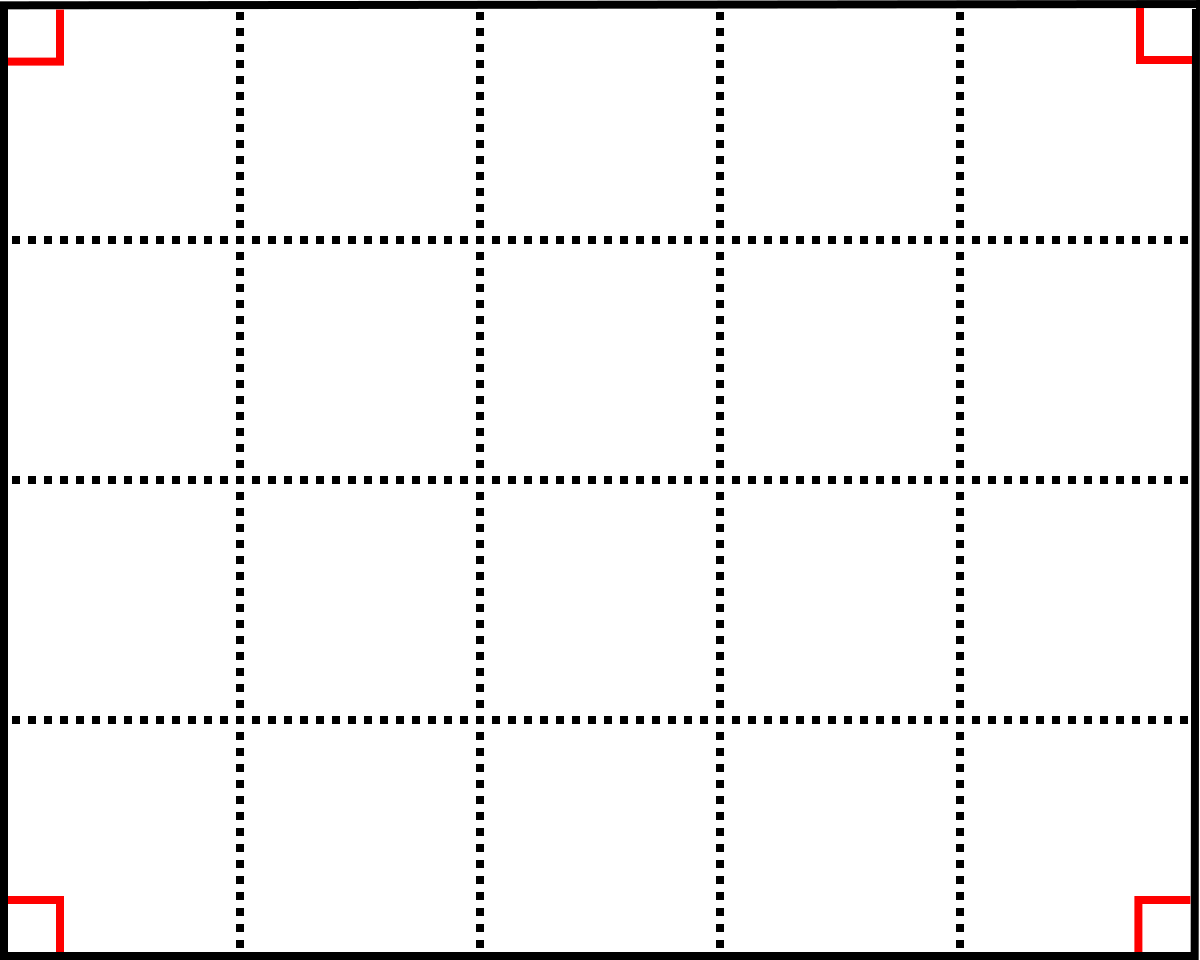
Un rectangle dont la longueur et la largeur sont égales à des nombres entiers m et n peut être vu comme composé de m lignes contenant chacune n carrés unité. Son aire est donc égale à m × n.
Si les dimensions du rectangle sont des fractions m⁄p et n⁄q, on considère qu'on a « découpé » le rectangle de dimensions m et n en p parts égales, puis chacune de ces parts à nouveau en q parts égales. Le rectangle de dimensions m et n contient donc p × q fois celui de dimensions m⁄p et n⁄q. L'aire de ce dernier rectangle est donc égale à m⁄p × n⁄q.
Ce résultat se généralise au cas où la longueur et la largeur du rectangle sont des nombres réels, mais le raisonnement est plus abstrait : il nécessite un passage à la limite, en considérant que tout nombre réel est la limite d'une suite de nombres rationnels.
- Cas particulier du carré
Un carré est un rectangle dont la longueur et la largeur sont égales à un même nombre appelé côté du carré. Un carré de côté c possède une aire égale à c × c, ce qui se note c2. Réciproquement, tout nombre de la forme c2 (où c est positif) peut être considéré comme l'aire d'un carré de côté c, ce qui explique que c2 se lit « c au carré » ou « le carré de c ».
Triangle
La formule de calcul de l'aire d'un triangle la plus courante est :
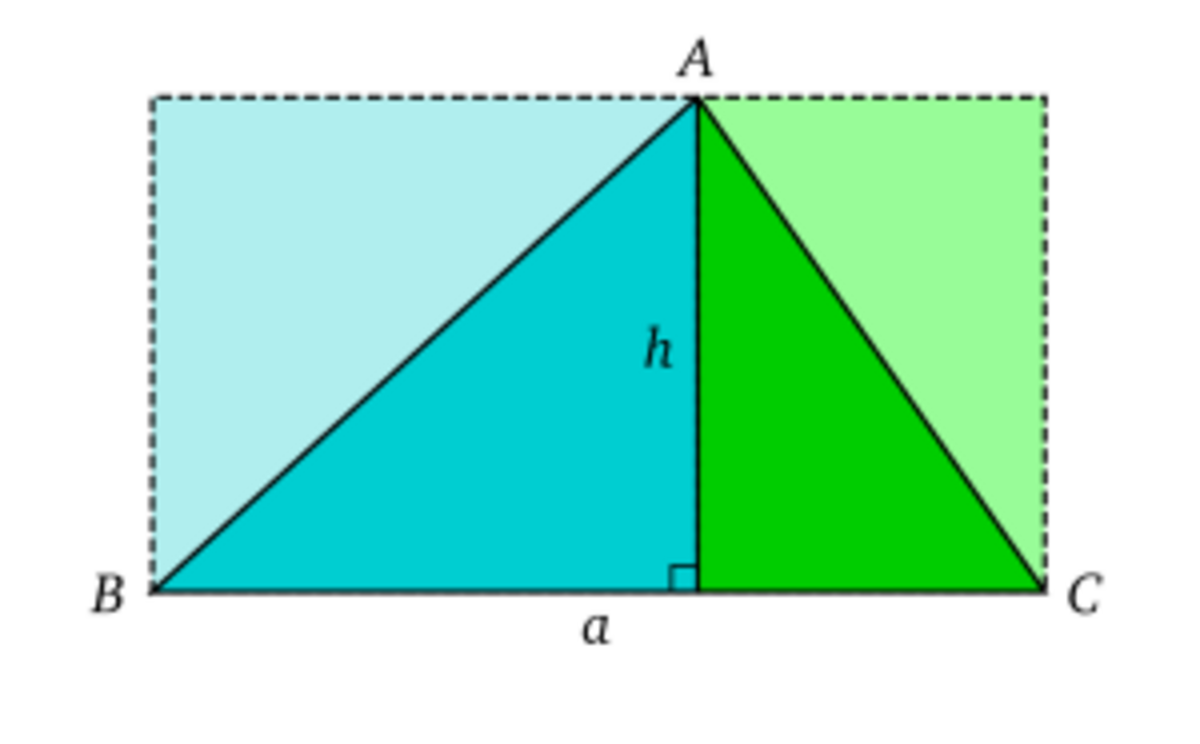
Aire d'un triangle — L'aire d'un triangle est égale à la moitié du produit de sa base par sa hauteur.
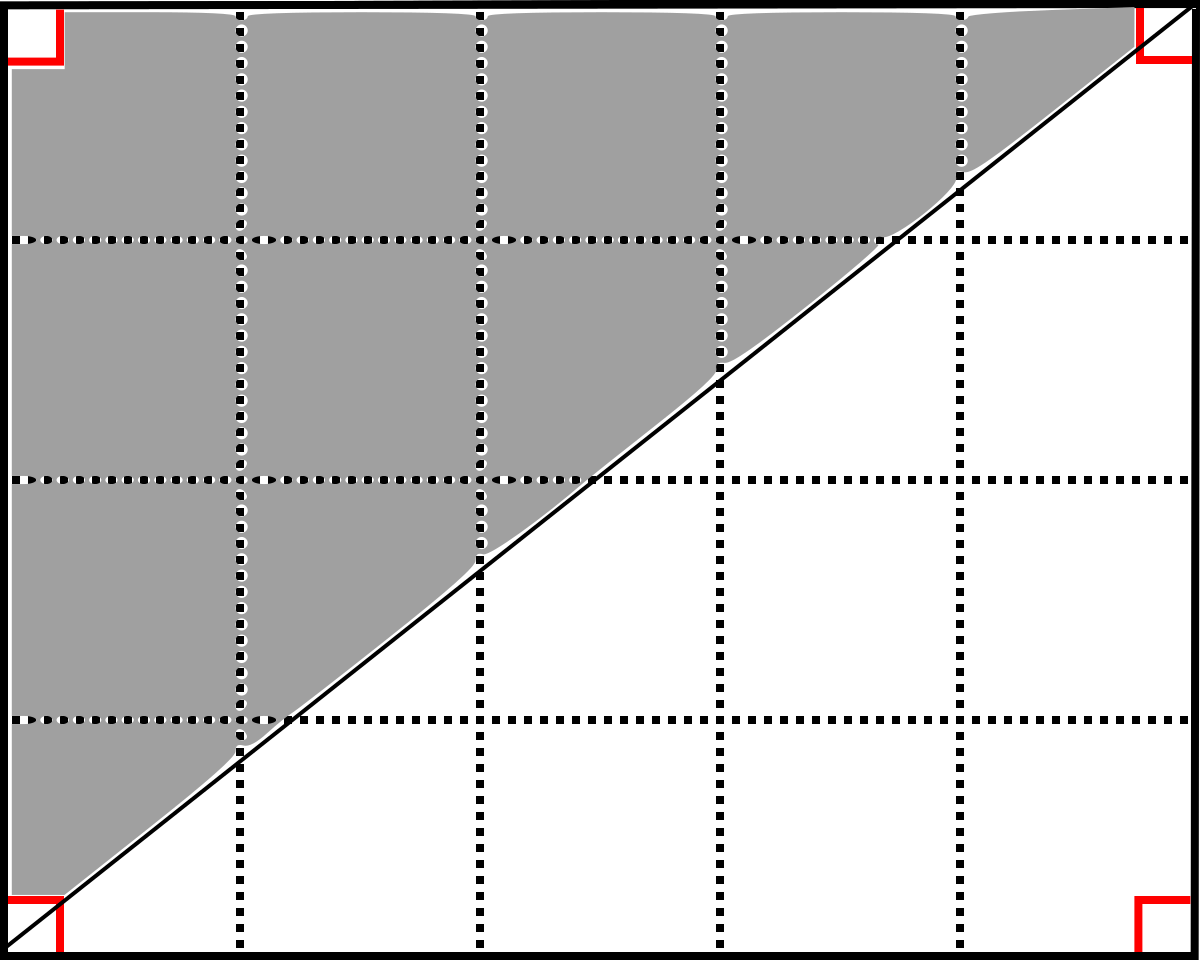
Tout triangle rectangle dont les cathètes (ou petits côtés) mesurent a et b peut être considéré comme la moitié d'un rectangle de dimensions a et b partagé en deux par une de ses diagonales. L'aire de ce triangle rectangle est donc égale à
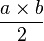
Plus généralement, tout triangle de hauteur d'un triangle h et de côté associé b (dans ce cas, le côté est appelé base) est la moitié d'un rectangle de dimensions h et b, ce qui donne la formule classique de calcul d'aire d'un triangle :
D'autres méthodes permettent de calculer l'aire d'un triangle et, par suite, de tout polygone en utilisant le fait que tout polygone peut être partagé en un nombre fini de triangles. C'est notamment en partageant un polygone régulier en triangles dont un sommet est son centre qu'on obtient les formules usuelles de calcul de l'aire d'un polygone régulier.
| En accolant au triangle rectangle gris un autre triangle isométrique suivant l'hypoténuse, on obtient un rectangle. |
Disque
Théorème — L'aire d'un disque de rayon R est égale à π × R 2.
La démonstration de ce résultat repose sur un passage à la limite en partageant le disque en une infinité de triangles.
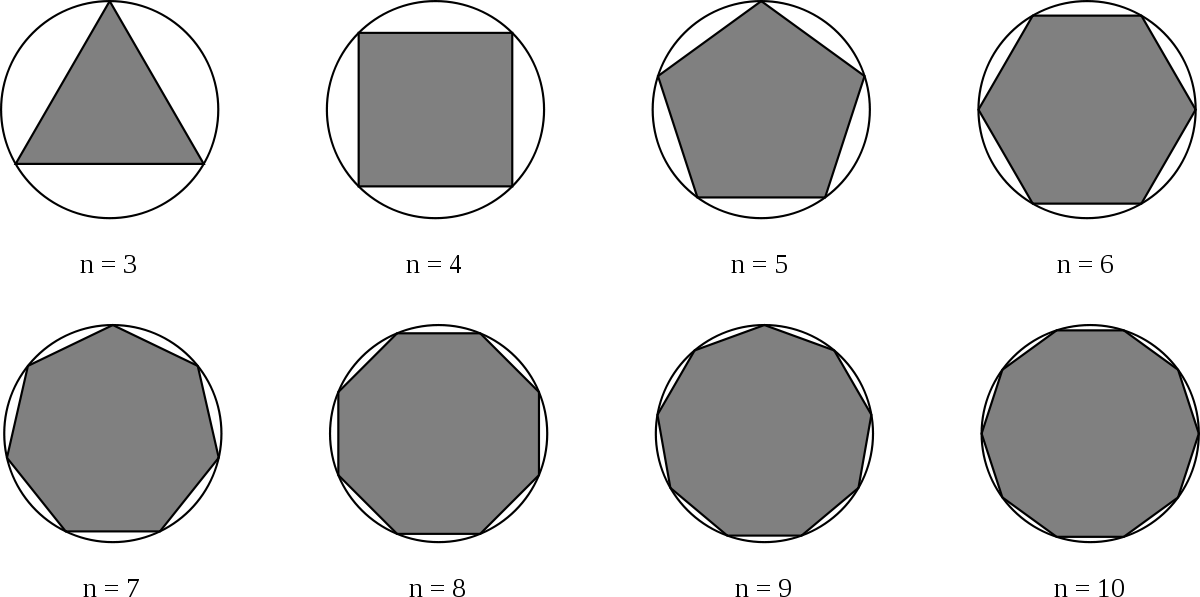
En considérant n points A1, A2, ... An régulièrement espacés sur un cercle de centre O et de rayon R, on obtient un polygone régulier à n côtés constitué de n triangles isocèles OA1A2, OA2A3, etc. Tous ces triangles ont une hauteur égale à R et les bases associées, pour tous ces triangles, sont égales à la distance A1A2. L'aire de chaque triangle est donc 1⁄2R × A1A2 et celle du polygone régulier A1A2...An est 1⁄2R × nA1A2. Lorsque le nombre n de points tend vers l'infini, le périmètre du polygone tend à se confondre avec celui du cercle dans lequel il est inscrit, donc nA1A2 tend vers 2πR. Ainsi, 1⁄2R × nA1A2 tend vers 1⁄2R × 2πR ce qui donne bien le résultat annoncé.
Intégrale
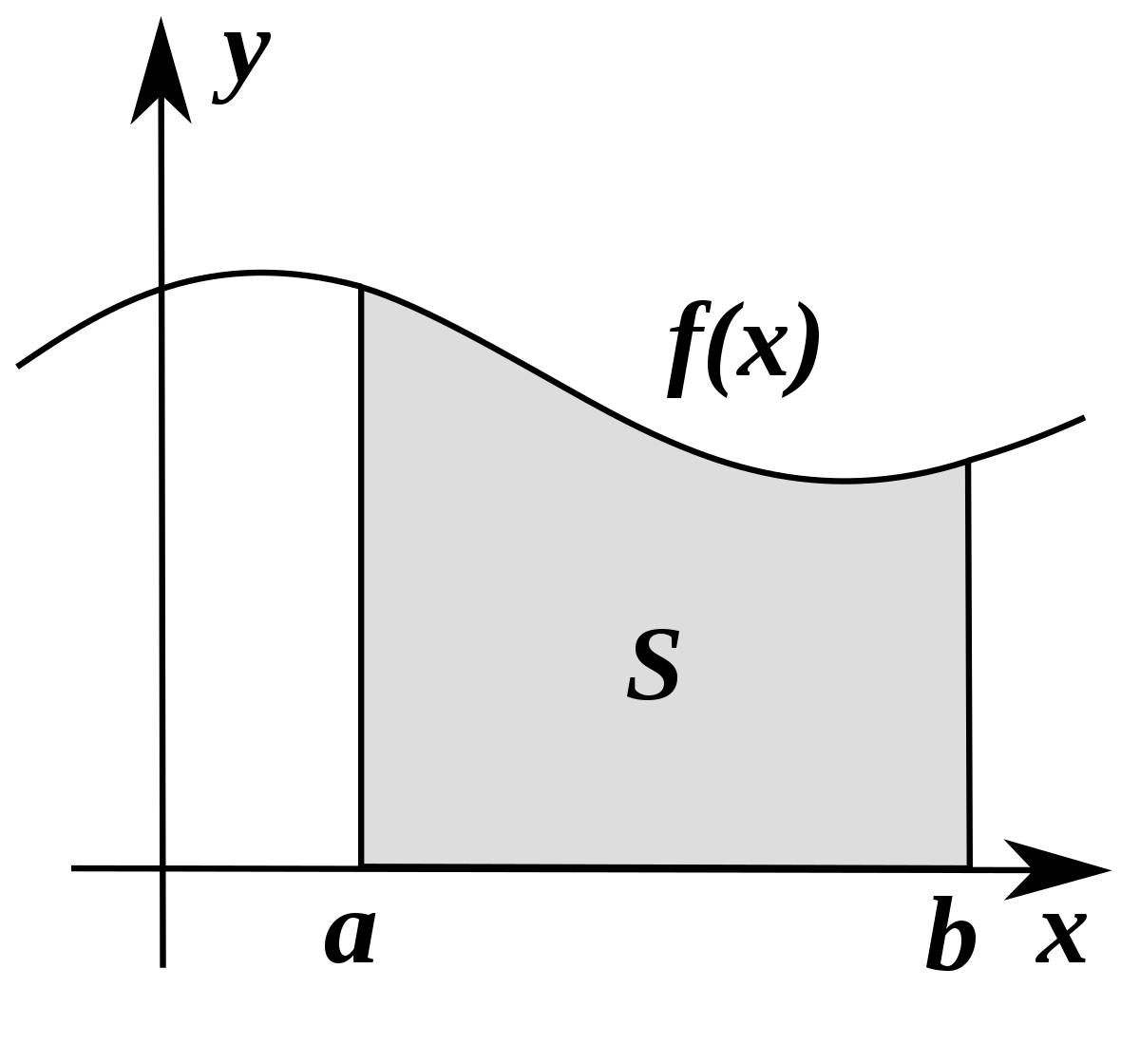
Le plan étant muni d'un repère orthonormé, pour une fonction numérique f positive et continue, l'intégrale de Riemann de f sur un intervalle [a ; b] est l'aire du domaine défini par :
- l'axe des abscisses ;
- les droites d'équation respectives x = a et x = b ;
- la graphe de la fonction f.
Cette intégrale est notée
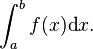
Cette aire peut être évaluée par des méthodes numériques en approchant l'aire sous la courbe par des surfaces usuelles : rectangles ou trapèzes notamment. Dans certains cas, un calcul de limite permet de déterminer la valeur exacte de l'intégrale, par un raisonnement semblable à celui utilisé ci-dessus pour le disque.
Un raisonnement mêlant des considérations sur les aires et du calcul différentiel permet de prouver que
où F est une primitive de f sur [a ; b]. Ainsi, la connaissance de primitives d'une fonction permet d'élargir l'ensemble des aires calculables par « découpage » vues précédemment.
Ainsi les raisonnements sur les aires et le calcul différentiel se nourrissent et s'enrichissent mutuellement. Les calculs d'aire ont de ce fait un retentissement sur de nombreux domaines des mathématiques, par le biais des intégrales, notamment les probabilités ou les statistiques par le calcul de la valeur moyenne d'une fonction.
Méthode de Monte Carlo
Si le calcul d'aires permet d'améliorer la connaissance de probabilités via les intégrales, la réciproque est également vraie. Soit une surface S, dont l'aire est connue, qui en contient une autre, L d'aire inconnue. La méthode de Monte-Carlo consiste à envoyer des points au hasard dans S. On dénombre alors le nombre total nS de points et le nombre nL qui se sont trouvés, par hasard, dans L. Il est alors probable que le rapport des aires de L et S soit proche du rapport de nL sur nS. La marge d'erreur sera statistiquement d'autant plus faible que le nombre de points nS sera grand.