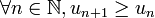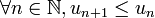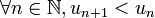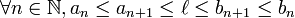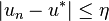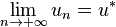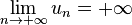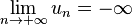Suite (mathématiques) - Définition

Suites réelles et relation d'ordre

Suites monotones

Définition

On dit qu'une suite réelle est monotone lorsqu'elle est croissante ou décroissante. Par extension, une suite réelle est dite strictement monotone lorsqu'elle est strictement croissante ou strictement décroissante.

Propriétés

• Suite croissante: On dira que la suite est croissante lorsque :

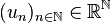
• Suite strictement croissante: On dira que la suite est strictement croissante lorsque :

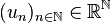
• Suite décroissante:On dira que la suite est décroissante lorsque :

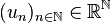
• Suite strictement décroissante: On dira que la suite est strictement décroissante lorsque :

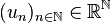
Exemples

La suite définie par U_n = 2n + 1 est strictement croissante sur .

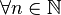
Critères

Propriété 1 : critère de croissance

Propriété 2 : critère de décroissance

Limites de suites monotones

Suite monotone bornée

L'axiome de la borne supérieure, permet de démontrer facilement :

Si est croissante (resp. décroissante) et majorée par M (resp. minorée par m), alors est convergente et .

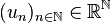
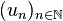
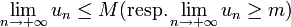
De cette propriété, découle la remarque suivante :

Si :

• est croissante
• est décroissante
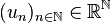
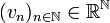
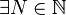
• tel que : on a

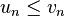
alors :

(u) et (v) sont convergentes et

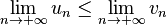
Suite monotone non bornée

Si est croissante (resp. décroissante) et non majorée (resp. non minorée ), alors tend vers (resp. )

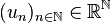
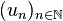
Suites adjacentes

Deux suites réelles et sont dites adjacentes lorsque :

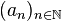
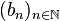
• l'une est croissante
• l'autre est décroissante
• la suite converge vers 0

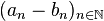
L'intérêt des suites adjacentes est qu'elles permettent d'une part de prouver l'existence d'une limite, d'autre part de fournir un encadrement de celle-ci aussi fin qu'on le souhaite. Ceci grâce aux deux propriétés suivantes:

• Si deux suites réelles et sont adjacentes, alors elles convergent et ont la même limite .
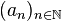
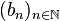
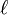
• De plus, en supposant croissante et décroissante on a :

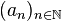
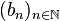
Limite de suite

Suite convergente

La notion de limite d'une suite est classique en topologie et les cas de convergence dans ou sont un cas particulier de cette définition. De façon simpliste, une suite a une certaine limite lorsque ses points se rapprochent de la valeur limite lorsque l'indice devient grand.

Définition générale :

Soit E un espace muni d'une topologie . On note l'ensemble des ouverts contenant u.
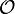
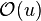
On dira que la suite est une suite convergente vers si

, tel que , .

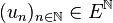
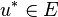
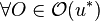
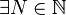
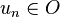
Cette définition se traduit plus simplement pour des suites convergente dans ou

Suite réelle convergente

On dira que la suite u est convergente vers u ^* lorsque pour tout , il existe tel que pour tout , n > N:

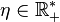
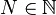
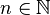
On dit alors que u tend vers u ^* , et on le note :

Suite complexe convergente

La même définition s'applique en écrivant, à la place d'une valeur absolue, un module.

Limites infinies

Pour les suites réelles, on élargit le champ des limites possibles aux deux limites infinies et avec les définitions suivantes

Définition 1 :

On dira que la suite u est divergente vers lorsque pour tout , il existe tel que pour tout , n > N:

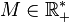
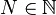
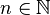
u_n > M

On dit alors que u tend vers , et on le note :

Définition 2 :

On dira que la suite u est divergente vers si, pour tout , il existe tel que pour tout , n > N:

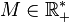
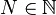
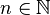
u_n < − M

On dit alors que u tend vers , et on le note :

Propriétés

Les propriétés sur les limites

• Unicité
• Opération
• Complétude

vont dépendre de l'espace sur lequel on travaille et sont détaillées dans l'article : Limite de suite.