Suite logistique - Définition

Commentaires

Quelques raisonnements simples et quelques graphiques permettent d'éclairer partiellement les résultats qui précèdent.

Graphiques

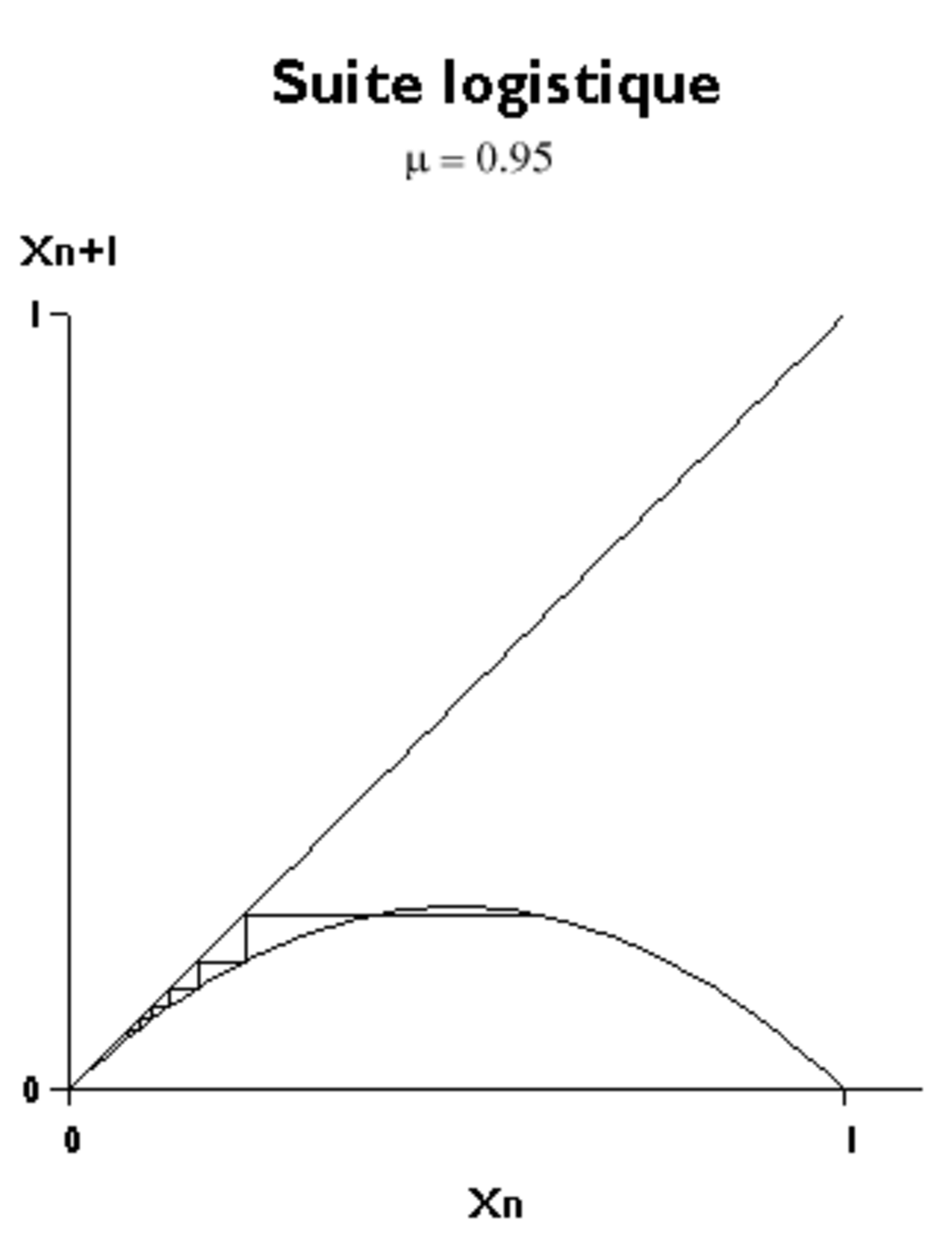
L'évolution de la suite logistique peut être représentée dans le plan (x_n, x_n+1).

L'équation de base représente une parabole qui passe par les points d'abscisses 0 et 1 sur l'axe horizontal. Pour que les valeurs de x_n+1 ne deviennent pas négatives, il faut ne retenir que l'arc compris entre ces deux points ; celui-ci présente, pour x_n = ½, un maximum de valeur μ/4. Cette valeur doit aussi être comprise entre 0 et 1, d'où μ < 4.

Si la suite converge, sa limite satisfait l'équation x_n+1 = x_n. Cette limite éventuelle, notée x, est solution de l'équation du second degré

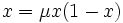
et peut donc prendre l'une ou l'autre des valeurs

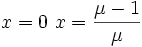
Pour décrire le comportement de la suite, il faut partir d'une abscisse x₀, déterminer sur la parabole la valeur x₁ qui est alors transformée en une nouvelle abscisse en passant par la bissectrice x_n+1 = x_n et répéter ces deux opérations.

Domaines de convergence

Pour certaines valeurs du paramètre μ, la suite se comporte comme une suite classique et converge vers l'une des deux limites possibles. L'équation de base peut se réécrire sous la forme

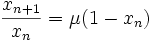
Si , la suite est majorée par une suite géométrique qui tend vers 0.

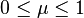
Pour voir le comportement vis-à-vis de la seconde limite éventuelle, il suffit d'effectuer le changement de variable x_n = u_n + 1 - 1/μ. La formule devient :

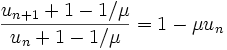
Dans ce cas, la condition de convergence exige que le second membre soit compris entre -1 et + 1 : .

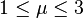
On vérifie que, si u_n est proche de la limite 1 - 1/μ, alors 1-μ u_n est proche de 2 - μ et u_n tend vers sa limite par valeurs croissantes si μ est inférieur à 2, par valeurs alternées s'il est supérieur à 2.

Bifurcations

Dans le paragraphe précédent, la formule de récurrence de la forme x_n+1 = f(x_n) a permis d'obtenir les premiers attracteurs en cherchant une limite éventuelle conforme à l'équation x = f(x).

Lorsque μ devient supérieur à 3, il faut chercher une solution à l'équation x = f(f(x)). Cela conduit à une équation du quatrième degré qui possède naturellement les racines déjà connues 0, 1-1/μ – mais ce ne sont plus des attracteurs – et la paire de nouvelles racines

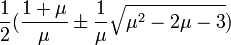
Il n'y a plus de convergence : un cycle-limite apparaît. Le résultat de l'itération bascule alternativement de l'une des deux dernières racines à l'autre : u_n+1 =u_n-1 tandis que u_n+2 =u_n. Pour μ = 3.4, les valeurs approchées successives 0.84, 0.45, 0.84, 0.45, 0.84.... apparaissent.

Au-delà de la limite de stabilité de ce cycle, √6 - 1, deux nouvelles bifurcations se produisent, qui dépendent des solutions de x = f(f(f(f(x)))). Pour μ = 3.47, les valeurs successives sont de l'ordre de 0.47, 0.86, 0.40, 0.84, 0.47,...

Chaos

De bifurcation en bifurcation, les évolutions deviennent de plus en plus complexes. Le processus aboutit, pour μ > 3.57 environ, à des systèmes qui ne présentent généralement plus d'attracteurs visibles. Les graphiques représentent alors une évolution «chaotique» au sens usuel du terme.

Cependant, dans le langage des mathématiciens, le mot chaos représente une forte sensibilité aux conditions initiales. Les deux graphiques correspondant à μ = 3.9 avec des valeurs initiales u₀ 0.100 et 0.101 montrent que les trajectoires s'éloignent l'une de l'autre jusqu'à devenir rapidement distinctes. Dans un problème concret les conditions initiales ne sont jamais connues exactement : au bout d'un certain temps, un phénomène chaotique est devenu imprévisible alors même que la loi qui le définit est parfaitement déterministe.