Srinivasa Ramanujan - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Formules
Ramanujan a donné la formule suivante :
Cette formule relie parfaitement une série infinie et une fraction continue pour donner une relation entre les deux plus célèbres constantes des mathématiques.
Jonathan et Peter Borwein ont démontré une deuxième formule qu'il avait découverte en 1910 :
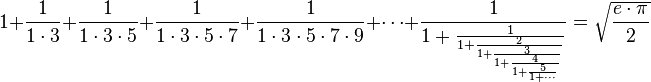
![\pi = \frac{9801}{2\sqrt{2} \displaystyle\sum^\infty_{n=0} \frac{(4n)!}{(n!)^4} \times \frac{[1103 + 26390n]}{(4 \times 99)^{4n}}}](https://static.techno-science.net/illustrationWebp/Definitions/autres/f/f47c56ad9410cd56d2004aa1557f9d7f_c10b3cbae21e06b2c49ec36fc918f48a.png)
Elle est très efficace puisqu'elle fournit 8 décimales à chaque itération.
