Sous-espace vectoriel - Définition
La liste des auteurs de cet article est disponible ici.
Intersection de deux sous-espaces vectoriels
Propriété
Soient
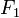
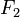
-
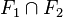
Plus généralement, toute intersection de sous-espaces vectoriels est un sous-espace vectoriel, c'est-à-dire que : pour toute famille
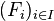
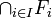
Sous-espace vectoriel engendré
Définition
Soit A une partie quelconque de E.
- Si A est non vide, on définit le sous-ensemble suivant de E :
-
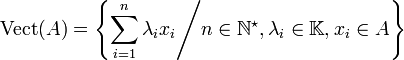
- (ainsi, Vect(A) est par définition l'ensemble des combinaisons linéaires d'éléments de A).
- On complète cette définition en posant
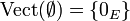
Propriété 1
Soit A une partie de E.
- L'ensemble Vect(A) est un sous-espace vectoriel de E, et il contient A.
- Si F est un sous-espace vectoriel de E contenant A, alors
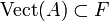
- C'est pourquoi on dit que Vect(A) est le plus petit sous-espace vectoriel de E contenant A.
- On l'appelle sous-espace vectoriel de E engendré par A.
- Le sous-espace vectoriel engendré par A est l'intersection de tous les sous-espaces vectoriels de E contenant A.
Nota : considérons l'application
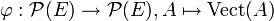
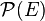
On désigne par A et B deux parties quelconques de E. Il résulte de la propriété précédente que :
- L'application

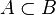
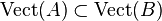
- L'application

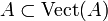
- L'application

- On dit alors que


- Pour qu'une partie A de E soit un sous-espace vectoriel de E, il faut et il suffit que Vect(A) = A.
Propriété 2
Soient A et B deux parties de E. Alors :
Somme de deux ou plusieurs sous-espaces vectoriels
Définition
Soient
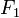
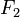
-
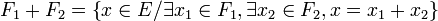
Propriété et définition
-
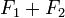
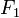
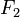
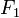
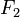
- Si F est un sous-espace vectoriel de E contenant à la fois
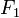
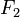
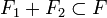
- C'est pourquoi on dit que
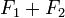
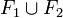
-
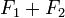
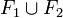
Remarque : la réunion de deux sous-espaces vectoriels n'est pas, en général, un sous-espace vectoriel ; pour qu'elle le soit, il faut et il suffit que l'un des deux soit inclus dans l'autre.
Généralisation
Soient
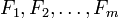
-
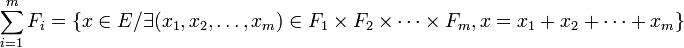
- C'est l'ensemble des vecteurs de E qui admettent au moins une décomposition en somme de vecteurs appartenant respectivement aux sous-espaces vectoriels
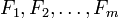
Dès lors :
-
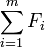
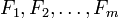
- Si F est un sous-espace vectoriel de E contenant à la fois
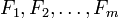
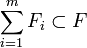
- On dit de même que
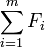
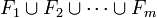
Espace vectoriel fini
Soit K un corps fini de cardinal q, et soit E un K-espace vectoriel de dimension finie n sur K. Alors l'ensemble E est fini de cardinal qn. Il possède un nombre fini de sous-espaces vectoriels. Le nombre de sous-espaces de dimension k vaut
-
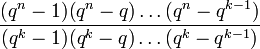
Cette quantité est le quotient du nombre de familles libres à k éléments de E par le nombre des bases dans un K-espace vectoriel de dimension k.
Etant de dimension n sur K, l'espace E est de cardinal qn. Il possède donc exactement qn-1 vecteurs non nuls. Il y a Or deux vecteurs v et w engendrent la même droite vectorielle ssi v et w sont colinéaires. Il y a q-1 vecteurs non nuls de E colinéaires à un vecteur non nul fixé. Le nombre de droites vectorielles de E est donc
-
-
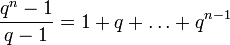
-
Si
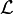
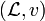
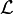
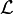
-
-
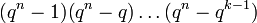
-
Il s'en suit que le nombre de bases d'un K-espace vectoriel de dimension k est
-
-
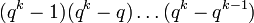
-