Somme des angles d'un triangle - Définition
La liste des auteurs de cet article est disponible ici.
En géométrie sphérique
On obtient une géométrie cohérente en conservant tous les axiomes de la géométrie euclidienne, sauf l'axiome des parallèles qui devient :
Axiome des parallèles en géométrie sphérique — Étant donnés une droite et un point extérieur à cette droite, il n'existe aucune droite parallèle à cette droite passant par ce point.
Autrement dit, deux droites sont, soit confondues, soit sécantes.
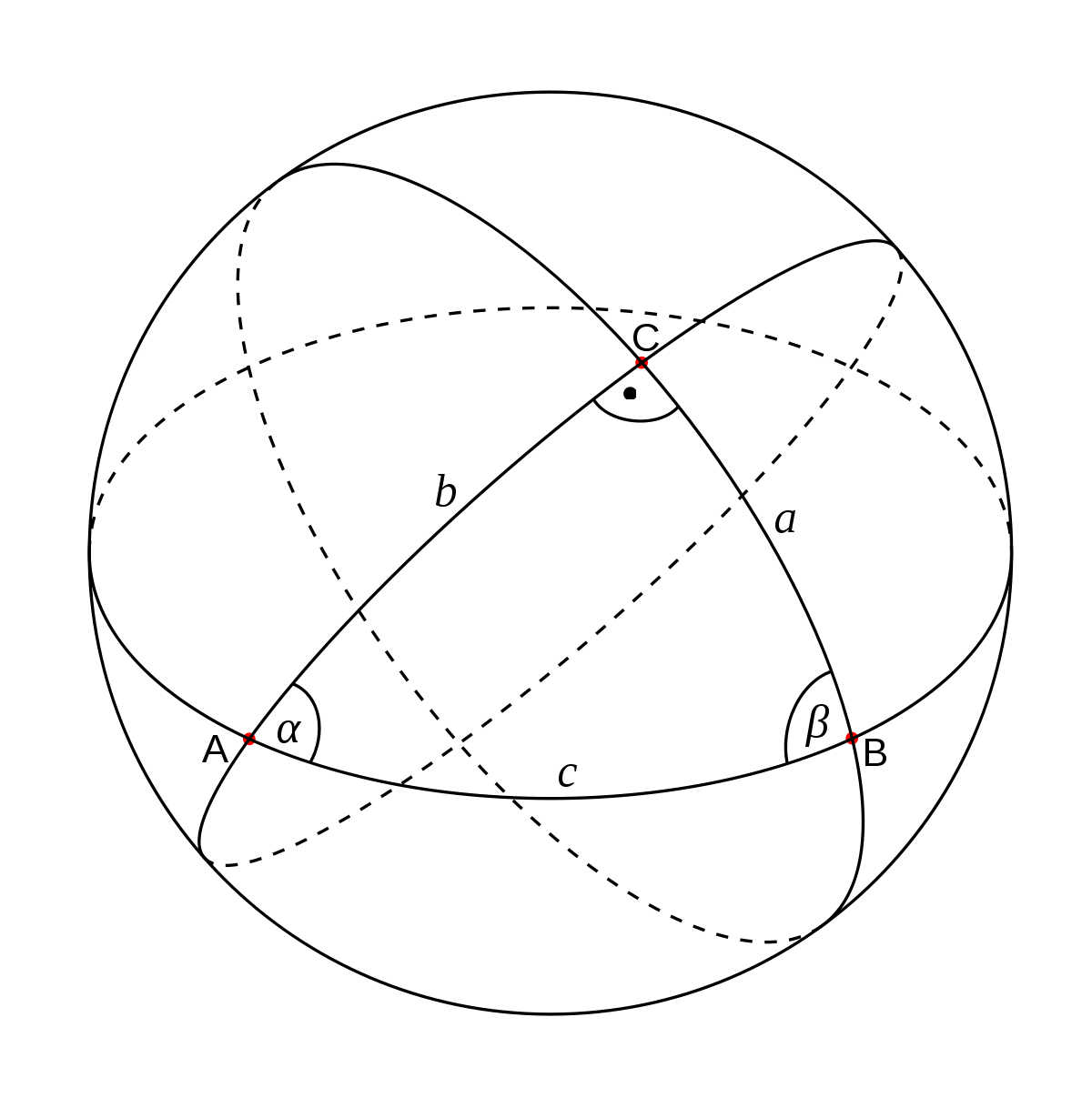
La géométrie sphérique correspond à ces axiomes. Elle est classiquement représentée par la géométrie d'une sphère en géométrie euclidienne, cette sphère correspondant au plan sphérique. Les droites (en géométrie sphérique) sont alors les grands cercles de la sphère, c'est-à-dire les intersections de la sphère avec des plans (au sens euclidien) passant par le centre de la sphère. Un angle entre deux droites sphériques est égal à l'angle formé par les deux plans euclidiens définissant ces droites.
Les résultats sont alors différents de la géométrie euclidienne, en particulier, la somme des angles d'un triangle sphérique n'est plus constante, mais la mesure d'un angle plat (π radians ou 180°) joue néanmoins un grand rôle :
Somme des angles d'un triangle en géométrie sphérique — La somme des angles d'un triangles est toujours supérieure à un angle plat.
La différence entre la somme des angles d'un triangle et la mesure d'un angle plat est proportionnelle à l'aire S du triangle. Soit, avec des angles exprimés en radians :
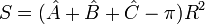
si la sphère est de rayon R, l'espace euclidien dans lequel elle est plongée étant muni de la distance usuelle.
Un triangle sphérique peut avoir deux ou trois angles droits. Un triangle sphérique équilatéral (avec trois côtés de même longueur) n'est pas forcément équiangulaire (avec trois angles égaux) et réciproquement. Par contre, si les angles de deux triangles sphériques sont égaux, alors leurs côtés sont égaux.
La formule de l'aire montre que, pour un triangle dont l'aire est très proche de zéro, la somme des angles est très proche de l'angle plat. Les résultats de la géométrie euclidienne donnent alors de bonnes approximations de ceux de la géométrie sphérique. En pratique, la géométrie sphérique est utilisée pour l'étude de planètes comme la Terre, notamment pour la navigation. Mais, pour des mesures ou des raisonnements sur des « petites » portions de planète (comme dans un jardin ou une ville peu étendue), la géométrie euclidienne donne des résultats satisfaisants.
Lien avec l'axiome des parallèles
La propriété de géométrie euclidienne doit se lire ainsi : la somme des angles de tout triangle est égale à deux angles droits. Elle se démontre en utilisant le postulat des parallèles, appelé aussi cinquième postulat d'Euclide, qui est :
Axiome des parallèles — Par un point, il passe une et une seule droite parallèle à une droite donnée.
Si on ôte cet axiome de la géométrie euclidienne, on obtient le résultat réciproque suivant, dû à Adrien-Marie Legendre :
Théorème de Legendre — Si il existe un triangle dont la somme des angles est égale à deux angles droits, alors cette somme est la même pour tous les triangles, et le cinquième postulat d'Euclide est vrai.
Autrement dit, il est possible de remplacer le cinquième postulat d'Euclide par un autre axiome : il existe un triangle dont la somme des angles est égale à deux angles droits. Alors, l'axiome des parallèles devient un théorème qu'on peut démontrer. Cette permutation ne change en rien les autres résultats de la géométrie euclidienne.