Ruban de Möbius - Définition

Définition par identification abstraite

Mathématiquement, on peut définir le ruban comme l'ensemble quotient de l'ensemble par la relation d'équivalence définie par : si et seulement si , muni de la topologie quotient. Par comparaison, un ruban « normal » (tronc de cylindre) serait défini par la relation .

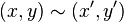
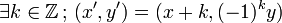
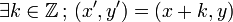
Cela permet de voir mathématiquement ce qui se passe quand on découpe le ruban : si est l'application de passage au quotient, est un cercle dont le complémentaire est connexe.

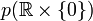
On peut aussi réaliser le ruban de Möbius comme le complémentaire d'un disque ouvert dans le plan projectif réel (vu comme la sphère après idendification des points diamètralement opposés).

La bande de Möbius chez Lacan

Dans le vocabulaire de Jacques Lacan : « 1962/63 - L'angoisse - 09/01/63 - Qu'est-ce qui fait qu'une image spéculaire est distincte de ce qu'elle représente ? c'est que la droite devient la gauche et inversement. - Une surface à une seule face ne peut pas être retournée. - Ainsi une bande de Mœbius, si vous en retournez une sur elle-même, elle sera toujours identique à elle-même. C'est ce que j'appelle n'avoir pas d'image spéculaire. »

Il convient de remarquer que, d'un point de vue mathématique, l'affirmation précédente de Lacan est erronée : on a vu dans les sections précédentes que l'image miroir d'un ruban de Möbius correspond à un retournement (avant collage) d'un demi-tour dans l'autre direction, et donc n'est pas identique au ruban initial.