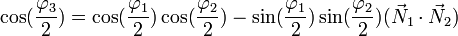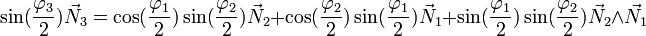Rotation vectorielle - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Soit E un espace vectoriel euclidien orienté réel de dimension finie n. Une rotation vectorielle de E est un élément du groupe spécial orthogonal SO(E). Si on choisit une base orthonormée directe de E, sa matrice dans cette base est orthogonale directe.
Rotation vectorielle plane
Écriture matricielle
Dans le plan, une rotation vectorielle est simplement définie par son angle
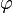
![\left[\begin{matrix}\cos\varphi&-\sin\varphi \\ \sin\varphi&\cos\varphi\end{matrix}\right]](https://static.techno-science.net/illustration/Definitions/autres/3/30459de218c3e4697fa643c971fa5468_feea1b9b6a1ff3579ff51619787400a6.png)
Autrement dit, un vecteur V de composantes
![\left[x ; y\right]](https://static.techno-science.net/illustration/Definitions/autres/2/241337597bef496c93c73f6a6864a0aa_a9f0707bf980d1690567b74d84777936.png)
![\left[x' ; y'\right]](https://static.techno-science.net/illustration/Definitions/autres/2/22b0fafe90b967b7b28c452f7bdea659_09ca39ddb64b540836e5937d22053508.png)
![\left[\begin{matrix}x'\\y'\end{matrix}\right] = \left[\begin{matrix}\cos\varphi&-\sin\varphi \\ \sin\varphi&\cos\varphi\end{matrix}\right]\left[\begin{matrix}x\\y\end{matrix}\right]](https://static.techno-science.net/illustration/Definitions/autres/f/f2e29c257fff5916ba3492799da6d926_92fc0afe3978cf3fb7aec3b47b05697f.png)
c'est-à-dire que l'on a :
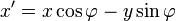
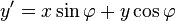
Écriture complexe
Remarque : ceci peut être rapproché de la formule suivante, écrite avec des nombres complexes :
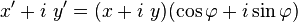
ou encore :
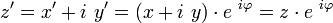
Sens de rotation
Lorsque


Composition
La composée de deux rotations vectorielles est une rotation vectorielle dont l'angle est la somme des angles des deux rotations, ce qu'on traduit en disant que le groupe des rotations vectorielles est isomorphe au groupe
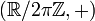
Rotations et angles
Dans la construction axiomatique de la géométrie, c'est la définition des rotations planes qui permet de définir la notion d'angle (voir l'article Angle).
Rotations en dimension 4
Les matrices du groupe orthogonal SO(4) peuvent de même se mettre sous forme canonique (après diagonalisation dans C) ; on montre qu'il existe deux plans vectoriels orthogonaux tels que dans une base orthonormale constituée de deux vecteurs de chaque plan, la matrice s'écrive
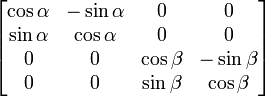
Rotation vectorielle dans l'espace de dimension 3
Écriture matricielle
Dans l'espace de dimension 3, une rotation vectorielle est définie par son axe
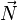
Nous supposerons que le vecteur
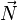
![\left[n_x ; n_y ; n_z\right]](https://static.techno-science.net/illustration/Definitions/autres/8/8945352b9188099436dcffbcb2f7593f_3488af1b67d453891b66b98f02906508.png)
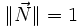
Soit
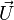
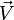
![\left[\varphi\,\,; \vec N\right]](https://static.techno-science.net/illustration/Definitions/autres/5/57cae6845640b4f52a9a9b972685e4fd_accf29075598b2a0590e899cbf0d3ce8.png)
Cas particulier simple
Commençons par l'étude du cas particulier où la base orthonormée directe
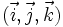
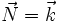
Soient
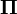
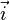
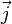
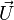
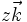
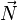
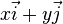

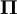
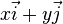
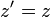
![\left[\begin{matrix}x'\\y'\end{matrix}\right] = \left[\begin{matrix}\cos\varphi&-\sin\varphi \\ \sin\varphi&\cos\varphi\end{matrix}\right]\left[\begin{matrix}x\\y\end{matrix}\right]](https://static.techno-science.net/illustration/Definitions/autres/f/f2e29c257fff5916ba3492799da6d926_92fc0afe3978cf3fb7aec3b47b05697f.png)
ce qui peut s'écrire sous la forme synthétique :
|
|
Cas général
Si le vecteur
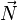
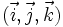
Comme ci-dessus, définissons le plan
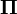
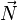
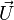
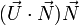
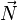
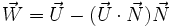
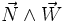
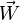

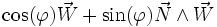
Finalement, l'image de
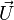
et si on remplace
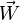
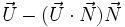
d'où finalement la formule d'Olinde Rodrigues :
|
|
La formule encadrée ci-dessus donne l'expression vectorielle du transformé
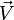
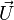
![\left[\varphi\,\,; \vec N\right]](https://static.techno-science.net/illustration/Definitions/autres/5/57cae6845640b4f52a9a9b972685e4fd_accf29075598b2a0590e899cbf0d3ce8.png)
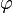
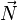
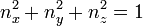
On peut présenter le même résultat sous la forme matricielle équivalente suivante :
![\left[\begin{matrix}x'\\y'\\z'\end{matrix}\right] = \left[\begin{matrix}M\end{matrix}\right]\left[\begin{matrix}x\\y\\z\end{matrix}\right]](https://static.techno-science.net/illustration/Definitions/autres/e/e718f5e6ae69f0bf3bd6bb86e1f18f26_4618973d10da54d23ca856640a61094c.png)
|
|
Remarques
La matrice M est appelée matrice de rotation. C'est une matrice orthogonale directe, ce qui signifie que ses colonnes forment une base orthonormée directe, ou encore que sa matrice transposée est égale à sa matrice inverse et que son déterminant vaut 1.
Inversement, étant donné une matrice de rotation quelconque, on retrouve facilement le cosinus de l'angle de rotation. En effet, la trace de la matrice (c'est-à-dire la somme de ses éléments diagonaux) est égale à
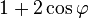
ce qui permet de retrouver rapidement l'axe et le sinus associés à la rotation. Géométriquement,
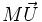
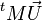
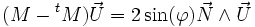
Utilisation des quaternions
On peut également faire appel à la notion de quaternions. En effet, on peut calculer le transformé
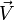
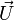
|
|
Composition de deux rotations vectorielles
La composée de deux rotations vectorielles
![\left[\varphi_1\,\,; \vec N_1\right]](https://static.techno-science.net/illustration/Definitions/autres/0/0afe8e3e2eb45bf56216a72b2e8abad3_1c58240ac34d7e1b5862756916b09b95.png)
![\left[\varphi_2\,\,; \vec N_2\right]](https://static.techno-science.net/illustration/Definitions/autres/2/2b202825053f63af493b76566bee86db_9654e5227769a6e1bc3a83c8e92b1b74.png)
![\left[\varphi_3\,\,; \vec N_3\right]](https://static.techno-science.net/illustration/Definitions/autres/8/8623622f284d4f59720591411417a78c_6d9ecce86d6a0b151209826e48374933.png)
On trouve que :
![\left[\begin{matrix}x'\\y'\\z'\end{matrix}\right] = \left[\begin{matrix}\cos\varphi&-\sin\varphi&0\\ \sin\varphi&\cos\varphi&0\\0&0&1\end{matrix}\right]\left[\begin{matrix}x\\y\\z\end{matrix}\right]](https://static.techno-science.net/illustration/Definitions/autres/d/d4b1a2fd3259d3e40f9fcb761ff034bd_cf56cd92d21978487815508aee445a8b.png)
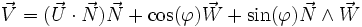
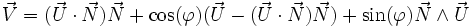
![\vec V = \cos\varphi\ \vec U + (1-\cos\varphi)(\vec U\cdot\vec N)\ \vec N + \sin\varphi\,\,\left[\vec N\wedge\vec U\right]](https://static.techno-science.net/illustration/Definitions/autres/c/c16a6af81c724c7631d1469df15eb38c_cfdf4cdbe6c15a6cc88a3779566d697f.png)
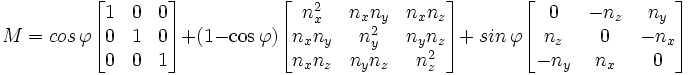
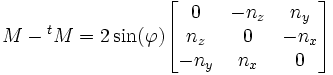
![(0,\ \vec V) = \left(0,\ \mathbf R_{\left[\varphi, \vec N\right]}(\vec U)\right) = (\cos \frac{\varphi}{2},\ \sin \frac{\varphi}{2}\ \vec N)\cdot (0,\ \vec U)\cdot (\cos \frac{\varphi}{2},\ -\sin \frac{\varphi}{2}\ \vec N)](https://static.techno-science.net/illustration/Definitions/autres/c/c72e2b0d527369117934b7ffc3fd1e98_95bfdc18e7479ec369f17550f54a419d.png)