Réversibilité et irréversibilité en thermodynamique - Définition

Définition

D'une manière générale on dit qu'un phénomène est réversible, si une modification infinitésimale des conditions permet à un système, qui a évolué sous l'influence de ce phénomène, de retrouver son état immédiatement antérieur. En thermodynamique par exemple, la notion d'évolution réversible est quantitative puisqu'on la définit comme une évolution pour laquelle aucune entropie n'est produite.

Par opposition, tous les autres phénomènes sont dits irréversibles. Ce sont ceux pour lesquels il est impossible de retrouver l'état immédiatement antérieur d'un système sans modifications importantes des conditions. Cela se traduit en thermodynamique par une production d'entropie.

Pour le physicien, tous les phénomènes sont irréversibles, et la réversibilité est un cas limite mathématique ou une idéalisation.

L'irréversibilité thermodynamique

C'est la thermodynamique, qui interprète les phénomènes macroscopiques à partir de leurs causes microscopiques, qui permet un traitement rigoureux et complet des irréversibilités, en élargissant certains concepts de la mécanique classique (notamment celui d'énergie) et en lui adjoignant de nouveaux principes (Second principe de la thermodynamique).

Conditions d'irréversibilité

• inhomogénéités des grandeurs intensives,
• brutalité et rapidité de la transformation,
• présence de phénomènes dissipatifs.

Les transformations réelles sont irréversibles à cause notamment de phénomènes dissipatifs. Le système ne peut pas « revenir en arrière » de façon spontanée. En thermodynamique ceci est formalisée dans le cadre du second principe par un terme de création d'entropie qui caractérise le fait que le désordre global (système + environnement) augmente ou bien encore qu'une partie de l'information sur le système a été perdue. Il est tout à fait possible pour le système de retourner à un état immédiatement antérieur à une transformation irréversible, mais cela nécessite l'action d'un opérateur extérieur.

Expression et interprétation

L’expression moderne du second principe formalise cette création d’entropie et permet de quantifier l'irréversibilité d'une transformation. Pour tout système fermé, la variation d'entropie au cours d'une transformation peut s'écrire :

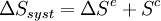
• Le terme correspond à l'entropie échangée entre le système et le milieu extérieur.

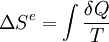
• Le terme est le terme de création d'entropie. Il est toujours positif et plus il est grand, plus la transformation du système étudié est irréversible. Dans le cas d'une transformation réversible (hypothétique), il est nul.

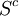
L'interprétation statistique de l'entropie et la théorie de l'information (avec notamment l'entropie de Shannon) fournissent également des interprétations à l'irréversibilité des transformations. Elle correspond :

• à une évolution spontanée de tous les systèmes vers l'uniformité ; quand toutes les grandeurs intensives décrivant le système sont uniformes, le système ne peut plus évoluer spontanément.

Exemple : quand un sucre se dissout dans une tasse de café, la concentration en sucre est initialement très hétérogène (infinie dans le sucre, nulle partout ailleurs), puis totalement homogène dans la tasse une fois que la dissolution a pris fin. La recomposition spontanée du morceau de sucre ne sera jamais observée.

• à une perte d'information sur l'état du système ; toutes les évolutions s'arrêtent lorsque le désordre du système est le plus grand possible.

Exemple : toujours lors de la dissolution du sucre, l'information sur l'état du système est celle-ci : le sucre est localisée dans le morceau, le café tout autour. A la fin de la transformation il est impossible de distinguer les localisations du sucre et du café, ce qui correspond à une perte d'information.

Remarques

• Au cours d'une transformation réelle, l'entropie d'un système peut diminuer mais il y a alors obligatoirement un transfert de chaleur et d'entropie vers le milieu extérieur. Néanmoins, le bilan entropique de l'ensemble (système + milieu extérieur) reste toujours positif. Exemple : lorsque l'eau gèle son entropie diminue (le solide glace est plus ordonné que l'eau liquide) mais ce phénomène s'accompagne d'un dégagement de chaleur (inverse de la chaleur de fusion). Il s'ensuit que l'entropie du milieu extérieur augmente et comme la transformation est irréversible le bilan entropique est positif.

Démontrons-le dans le cas d'un système composé d'un vase contenant de l'eau liquide que l'on place à l'air libre à -10 °C soit 263 K. L'eau gèle à 0 °C (273 K) et tant qu'il y a coexistence de glace et d'eau liquide cette température de changement d'état reste constante et égale à 273 K. La chaleur de solidification de l'eau L_(solid) est négative ainsi que l'entropie de solidification ΔS_(syst) = L_(solid) / 273 < 0. En revanche, la chaleur est reçue par le milieu extérieur dont la température n'est pas affectée par le système beaucoup plus petit. Elle reste constante et égale à 263 K. La variation d'entropie du milieu extérieur est alors égale à ΔS_(ext) = - L_(solid) / 263 > 0.

Calculons le bilan entropique :

ΔS_(syst) + ΔS_(ext) = ( L_(solid) / 273 ) + ( -L_(solid) / 263 ) = L_(solid) ( 1/273 - 1/263 ). Comme L_(solid) < 0, il s'ensuit que le bilan est positif et l'entropie créée sera d'autant plus grande que l'écart des températures sera grand ainsi que l'irréversibilité qui va de pair. Si la température du milieu extérieur était très proche de 273K à -ε près, on se rapprocherait d'une transformation réversible et le bilan entropique serait proche de zéro.

• Les transformations réelles sont irréversibles, donc l'entropie de l'univers ne peut qu'augmenter. Cette constatation est conforme avec la théorie de l'expansion de l'univers. En effet en augmentant de volume depuis le Big Bang, l'univers devient de plus en plus désordonné et donc son entropie augmente.