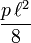Résistance des matériaux - Définition

Sollicitations

Sollicitations élémentaires

Type	Commentaire	Exemple
Traction	Allongement longitudinal, on tire de chaque côté	barre de remorquage
Compression	Raccourcissement, on appuie de chaque côté	poteau supportant un plancher
Cisaillement	Glissement relatif des sections	goujon de fixation
Torsion	Rotation par glissement relatif des sections droites	arbre de transmission d'un moteur
Flexion simple	Fléchissement sans allongement des fibres contenues dans le plan moyen	planche de plongeoir
Flexion pure ou circulaire	Fléchissement sans effort tranchant dans certaines zones	partie de poutre entre deux charges concentrées

Quelques notations et définitions

La terminologie employée suivant la grandeur étudiée dépend du point de vue par rapport à la pièce étudiée.

grandeur	point de vue extérieur	point de vue intérieur
mécanique	efforts	contraintes
géométrique	déplacements	déformations

Les efforts (ou chargement) regroupent les forces [N, kN ou MN] et les moments [Nm, kNm ou MNm]. Les déplacements sont l'ensemble des translations [unités de longueur compatibles avec celles utilisées pour les moments] et des rotations [rad].

Contraintes mécaniques élémentaires

• Loi de Hooke simplifiée à une seule dimension

La contrainte normale σ est proportionnelle à l’allongement relatif et un facteur constant E désigné sous le nom de module d'élasticité ou encore module d'Young :

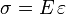
σ s'exprime en Pa ou N/m² et plus souvent en MPa ou N/mm² ;

E est homogène à une contrainte [Pa] ;

est sans dimension.

L’allongement relatif est le rapport entre longueurs initiale et finale

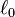
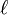
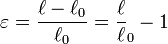
• Traction / Compression

Cette contrainte est dite contrainte normale due à la force de traction. σ [Pa] est égale à l'intensité de la force F [N] divisée par l'aire S [m²] de la surface normale à cette force :

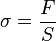
• critère de contrainte maximale: .

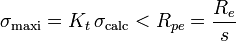
R_e : Résistance élastique
K_t : coefficient de concentration. K_t dépend de la géométrie de la poutre (ex: pour une vis à filets triangulaire K_t = 2,5)
est un coefficient de sécurité (ex: pour les gaines d'un ascenseur s = 12).

• Flexion

Sous l'effet du moment de flexion [N.m], la contrainte de flexion à une distance [m] de la fibre neutre s'exprime en fonction du moment quadratique [m⁴] de la section étudiée par la relation :

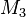
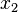
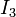
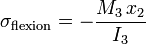
avec , moment quadratique, qui est habituellement désigné par inertie de la section par rapport à l'axe du moment de flexion.
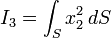
Pour une section rectangulaire : (b:base, h:hauteur).
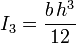
Pour une section circulaire : .

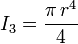
Le théorème de Huygens permet de calculer le moment quadratique d'une section coupée en plusieurs morceaux:

.

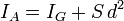
• Cisaillement

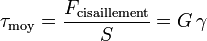
avec le module de Coulomb [Pa] : .

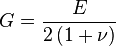
Pour avoir la contrainte tangentielle maximale :

• pour une section rectangulaire :
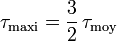
• pour une section circulaire :

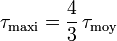
• Torsion

Ce qui suit concerne uniquement les poutres à sections circulaires.

où est l'angle unitaire de torsion (en rad/m).

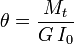
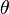
Le moment quadrapolaire de la section est donné par : .

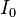
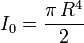
On peut aussi calculer avec .

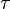
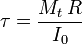
• critère de déformation: (rad/mm) (°/m)
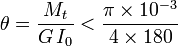
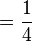
• critère de contrainte maximale: .

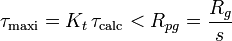
• Étude de la déformation d'une poutre fléchie

On peut obtenir l'allure de la déformée de la poutre en flexion à partir de l'équation différentielle

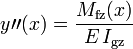
En intégrant 2 fois, et en déterminant les constantes, il est possible de trouver la forme de la déformée de la poutre en flexion.

Références théoriques

• La contrainte normale σ : contrainte
• L’allongement relatif  : tenseur des déformations
• Le module d’élasticité longitudinal E ou module de Young : module de Young
• Le module de cisaillement G ou le module d’élasticité tangentiel ou encore module de glissement : module de cisaillement
• Le coefficient de Poisson ν : coefficient de Poisson
• L'inertie I : moment d'inertie

Contraintes mécaniques composées

Type	Commentaire	Exemple
Flexion et torsion		arbre de transmission
Flexion et traction		vis
Flexion et compression	le flambage provoque les mêmes effets	poteau d'angle
Cisaillement et compression		pile de pont en rivière navigable
Cisaillement et traction		boulon précontraint

La poutre est généralement composée d'un matériau isotrope homogène et chargée dans son plan moyen, vertical le plus souvent. Dans ces conditions, l'ensemble des efforts extérieurs appliqué d'un côté d'une section droite quelconque se ramène à :

• un effort longitudinal de compression ou traction : l'effort normal ;
• un effort normal de cisaillement : l'effort tranchant ;
• un moment fléchissant.

Ce sont les éléments de réduction des charges extérieures au droit de la section considérée.

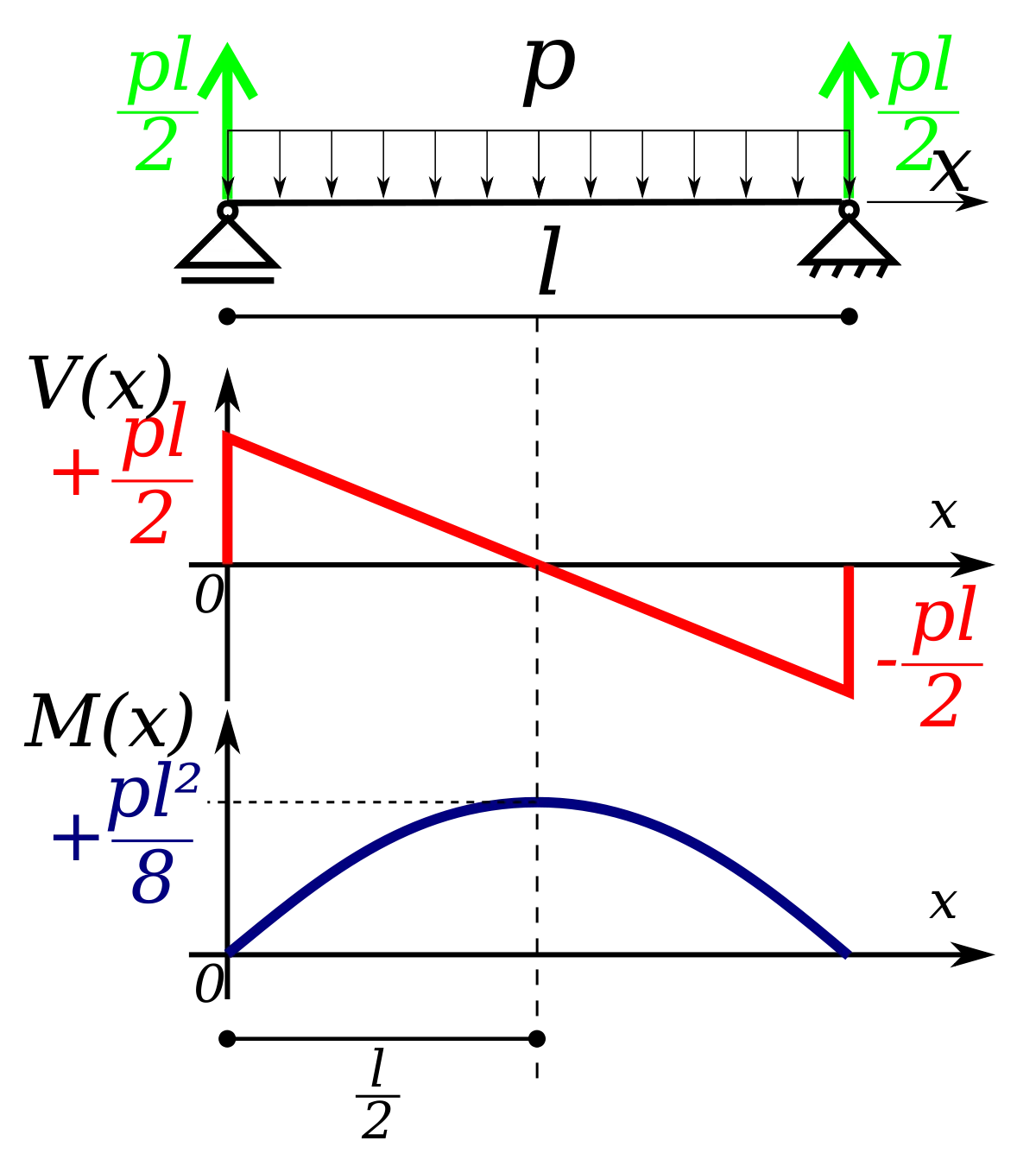
Un cas simple est constitué par une poutre droite, horizontale, de section constante, chargée uniformément et reposant sur deux appuis simples. Si on désigne par p la charge linéaire et par la longueur de la poutre, la détermination des éléments de réduction des efforts tient en quelques formules simples :

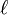
• la réaction à chaque appui est une force verticale, égale à la moitié de la charge totale soit ,
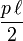
• l'effort tranchant varie linéairement de à avec une valeur nulle en milieu de travée. On doit vérifier que la contrainte de cisaillement au voisinage de l'appui reste inférieure à la résistance au cisaillement du matériau,
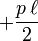
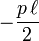
• Le moment fléchissant est nul sur appui et maximum en milieu de travée où il vaut . On doit vérifier que les contraintes dans la section à mi-travée ne dépassent ni la résistance à la compression, ni la résistance à la traction du matériau.