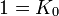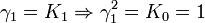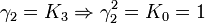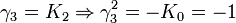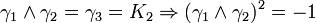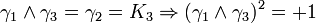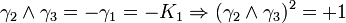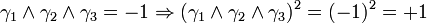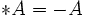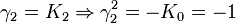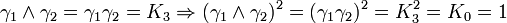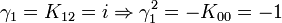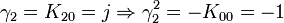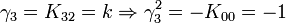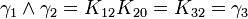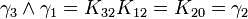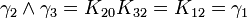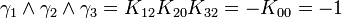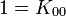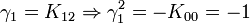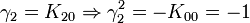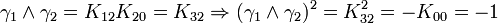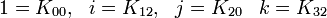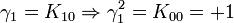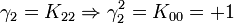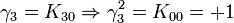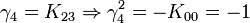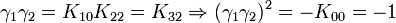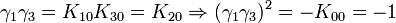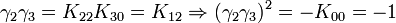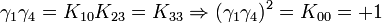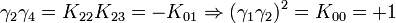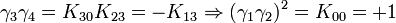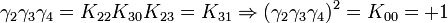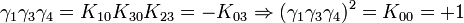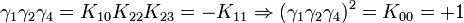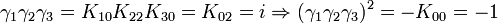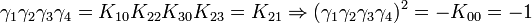Représentation des algèbres de Clifford - Définition

L'algèbre de Clifford R2,1

p = 2 et q = 1 donc 2 Kplus et 1 Kmoins pour base de vecteurs

catégorie 0 (le scalaire)

catégorie 1 (les vecteurs)

La signature est ( + + - )

catégorie 2 (les bivecteurs)

catégorie 3 (le pseudoscalaire)

Ceci est le premier exemple d'une algèbre de Clifford non-universelle puisque p+q = 3 et nous avons seulement 2² éléments et non 2³. La raison est très simple, chaque matrice est utilisée deux fois, une fois comme vecteur et une fois comme bivecteur. Et le pseudoscalaire est réel, comme le scalaire.

(Le dual de Hodge de chaque élément est simplement le négatif de l'original)

L'algèbre de Clifford réelle R1,1

p = 1 et q = 1 donc nous avons besoin d'une Kplus et d'une Kmoins comme base de vecteurs

Catégorie 0 (le scalaire)

catégorie 1 (les vecteurs)

catégorie 2 (le pseudoscalaire)

Ici encore, nous avons 2ⁿ éléments dans l'algèbre avec n = p+q donc elle est encore une algèbre de Clifford universelle.

L'algèbre de Clifford R0,3

p = 0 et q = 3 donc nous avons besoin de 3 matrices Kmoins comme base de vecteurs, ceci est la manière usuelle de travail avec les quaternions i, j et k sont maintenant des base de vecteurs et ijk = -1 est le pseudoscalaire. Cette algèbre est de nouveau isomorphe avec (les quaternions)

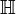
catégorie 0 (le scalaire)

catégorie 1 (les vecteurs)

La signature est ( - - - )

catégorie 2 (les bivecteurs)

catégorie 3 (le pseudoscalaire)

Un nombre de Clifford est ici, de nouveau, une combinaison linéaire de 4 éléments 1 i j et k. L'usage de -1 comme pseudoscalaire (ijk) est comme nous l'avons employé, mais il fait de cette algèbre un nouvel exemple d'algèbre de Clifford non-universelle, puisque p + q = 3 et nous avons seulement 2² éléments.

L'algèbre de Clifford R0,2

Ici p = 0 et q = 2 donc nous avons besoin de matrices Kmoins anticommutatives pour base de vecteurs. Ceci n'est pas possible avec des matrices réelles 2 x 2 donc nous avons besoin d'utiliser des matrices 4 x 4, et il existe beaucoup de possibilités. Cette algèbre est isomorphe avec l'anneau des quaternions.

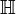
catégorie 0 (le scalaire)

catégorie 1 (les vecteurs)

La signature est (- -)

catégorie 2 (le pseudoscalaire)

L'isomorphisme avec les quaternions est comme suit :

1 est scalaire, i et j sont les vecteurs et k = ij est le pseudoscalaire.

Un nombre de Clifford est une combinaison linéaire de quatre éléments 1, i, j et k

L'utilisation de k comme pseudoscalaire ( i x j ) est un peu étrange mais sonne parfaitement.

L'algèbre de Clifford réelle R3,1

Ceci est pour moi l'algèbre de Clifford la plus intéressante parce qu'elle permet la construction des équations ressemblant aux équations de Dirac sans nombres complexes. Majorana l'a découverte. Par conséquent, les spineurs réels sont appelés les spineurs de Majorana. L'algèbre est aussi connue sous le nom d'algèbre de Majorana. Elle se sert de toutes les 16 matrices réelles 4 x 4. Les quatre bases de vecteurs sont en fait les trois matrices de Pauli (Kplus) completées d'une quatrième matrice antihermitienne (Kmin). La signature est ( + + + - ). Voir la convention de signe. Pour la signature ( + - - - ) ou ( - - - + ) souvent utilisée en physique, vous avez besoin de matrices complexes 4 x 4 ou matrices réelles 8 x 8 parce que vous ne pouvez pas former 3 matrices anticommutatives Kmoins 4 x 4. Voir R_1,3 pour différentes représentations.

catégorie 0 (le scalaire)

catégorie 1 (les vecteurs)

La signature est ( + + + - )

catégorie 2 (les bivecteurs, trois rotations et trois accélérateurs)

catégorie 3 (les pseudovecteurs, les duaux de Hodge des vecteurs)

la dernière est le pseudoscalaire dans R_3,0

catégorie 4 (le pseudoscalaire)